跳转至

Topic 9：活跃变量分析

约 2372 个字 3 行代码 11 张图片 预计阅读时间 8 分钟

Outline

1. 数据流分析

1.1 编译器优化

编译器优化的粒度一般分为下面三种：

  • Local/局部：只在单个基本块内或少量基本块间（在一个过程内的几个基本块）做优化；
  • Intraprocedural/Global/单函数内：在整个函数/过程内做优化；
  • Interprocedural/Whole-program/全程序：在从一个过程内到整个程序上的尺度做优化，有时候在链接时进行优化/Link Time Optimization/LTO。

在分析阶段，我们会对中间表示进行分析，收集一些程序的基本事实，比如指针指向、变量取值范围，定义使用关系等等；我们也会应用一些变换，比如常量折叠、死代码消除、循环不变式代码外提、寄存器分配等等。

在不同级别，编译器使用不同形式的 IR 执行分析和优化：

  • 局部级别，我们使用依赖图/Dependence Graph 进行优化；
  • 单函数内，我们使用控制流图/Control Flow Graph 和数据流方程进行优化；
  • 全程序，我们使用调用图/Call Graph 和函数间控制流图/Interprocedural Control Flow Graph 等进行优化。

1.2 数据流分析

控制流图（这里的定义和在 Topic 7：基本块与 Trace 中的不同），定义为一个有向图，其节点是语句，边表示控制流，语句可以是复制语句 x = [y] op z、拷贝语句或者分支语句。

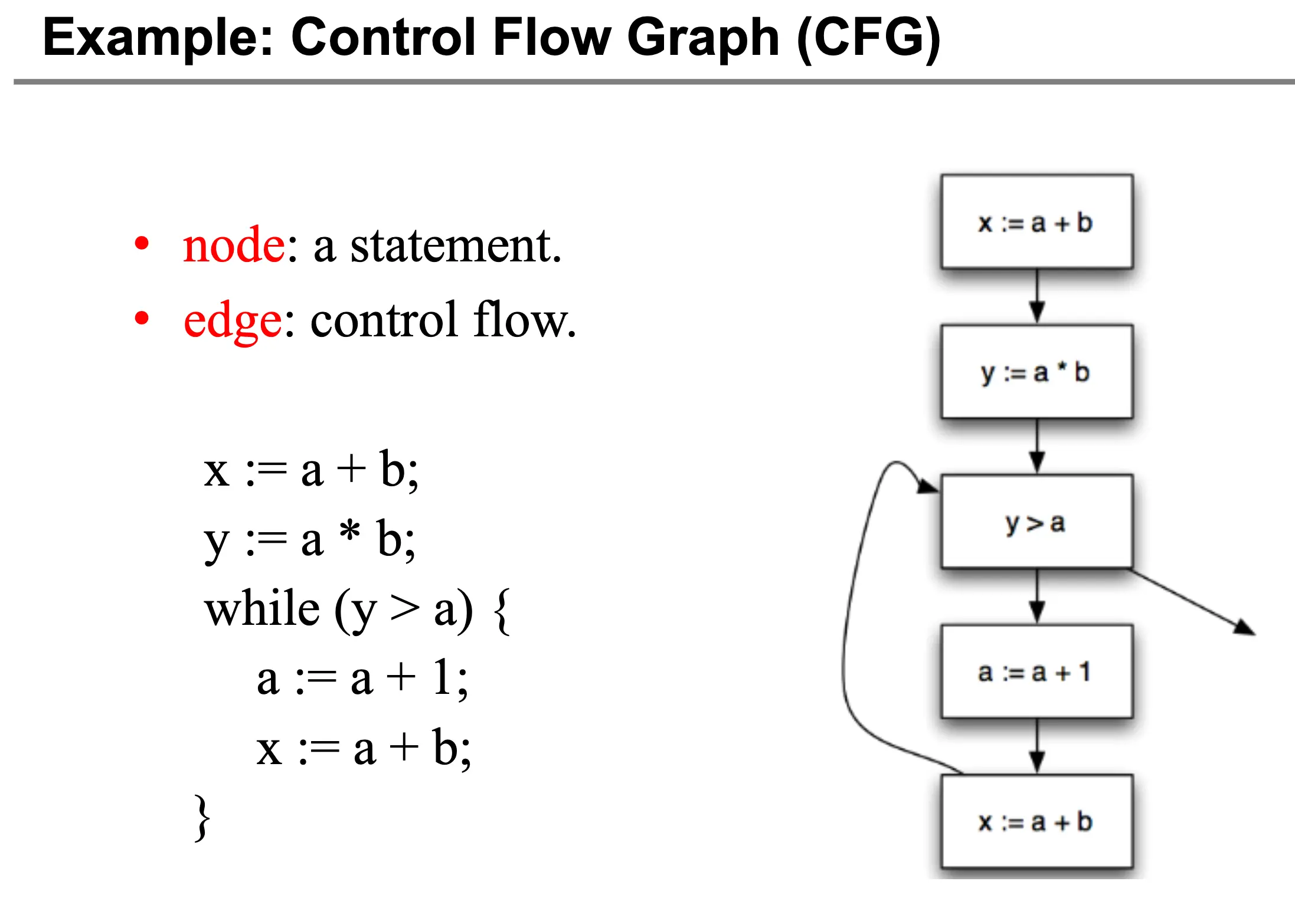
control flow graph

回忆基本块的定义，基本块是具有单一入口和单一出口的语句序列，我们可以将一些语句组合成一个基本块，这样控制流图的定义就和第七节的定义一致了，但是在这一节我们仍然使用单语句基本块。

数据流分析/Dataflow Analysis 可以在不执行程序的前提下，推导出关于程序的动态行为的信息，这些信息统称为数据流事实/Dataflow Facts，比如活性、类型、可达性等等。在程序验证和编译器优化都有应用。

变量的活性/Liveness：一个变量 x（的值）在语句 s 处是活的，当且仅当：

  • 存在后续语句 s' 使用 x；
  • 从 s 到 s' 存在一条路径，且这条路径上没有重新定义 x；

liveness

需要清楚的是，我们不能够准确地计算出变量的活性，考虑下面代码：

1
2
3
x = 10;
func();
return x;

我们无法确定 func() 是否会返回，因此我们无法确定 x 是否活。这基于停机问题/Halting Problem 的不可判定性，因此变量活性的准确计算问题就也是不可判定的。

莱斯定理/Rice Theorem：对任何的非平凡的程序性质，都不可判定，原因也是类似的。无论是检测某处变量是否是活的，还是计算更复杂的语义特性，都无法精确计算。因此编译器只能进行进行近似，比如对于一个 if 分支，我们假设这个分支会走两条路。

对于活性分析，我们使用过度近似/Overapproximate，将后续所有可能使用的变量都标记为活，虽然可能会产生假活，但是至少不会漏掉所有的活定义。

2. 活跃变量分析

2.1 活跃变量分析的价值

从寄存器分配的角度来看，指令选择后的低级中间表示/抽象汇编通常假设有无限多个寄存器，而寄存器分配的目标是将抽象汇编中的无限多个变量映射到优鲜多的真实的寄存器上，为了实现这个目标，需要先完成一次活性分析，检查每个变量的活跃区间。

对于下面的代码，假设目标机器只有一个寄存器 r，问题在于是否可以将 a、b、c 这三者全部放到同一个寄存器 r？先进行活跃分析，得到活跃区间，发现活跃区间并不重叠，这就可以将它们全部放到同一个寄存器 r 中，并且进行代码重写了。

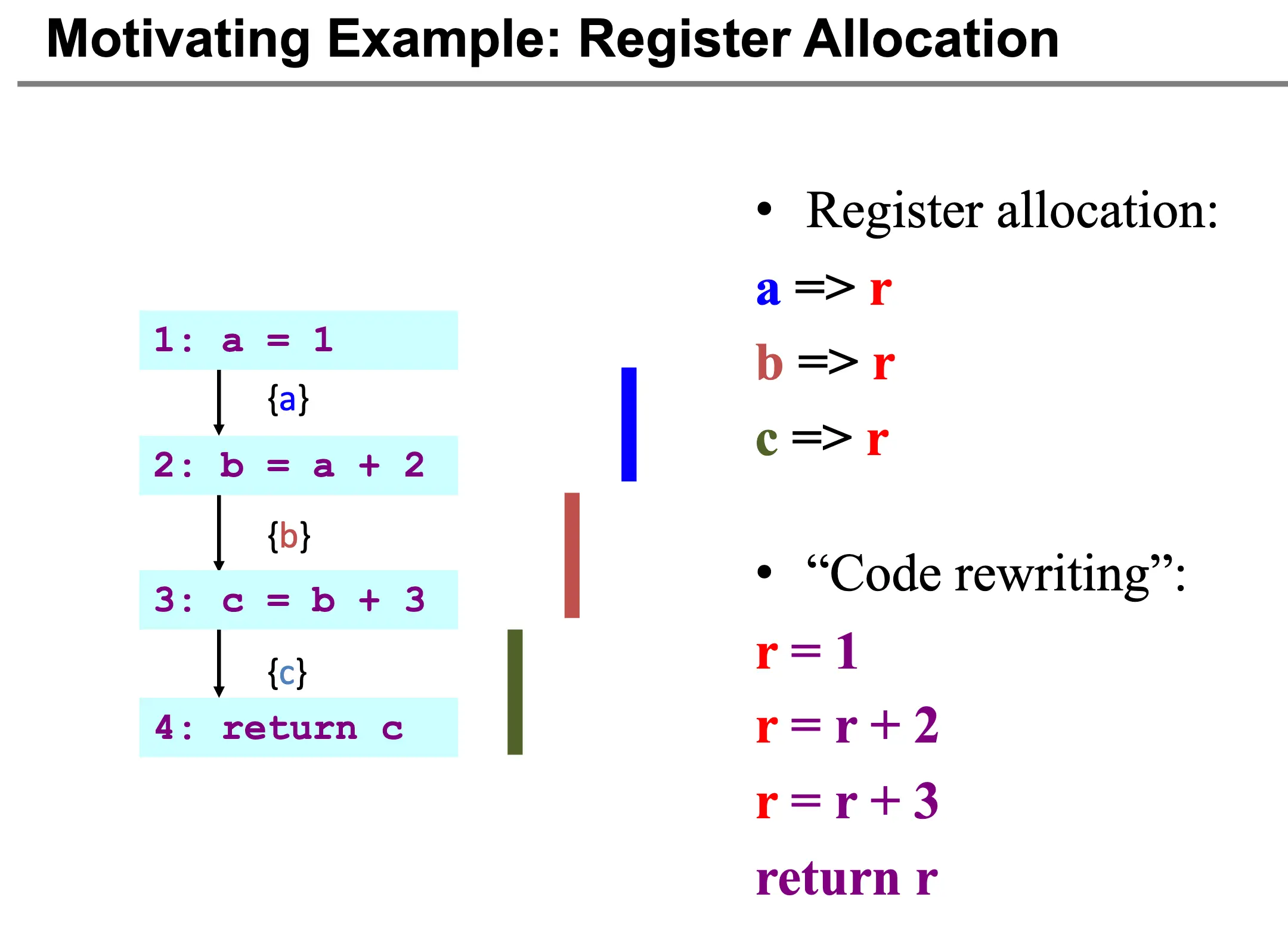
liveness

除此之外，活跃分析还在代码优化（移除无用赋值）、SSA 构造、安全性检查中有用。

2.2 数据流方程

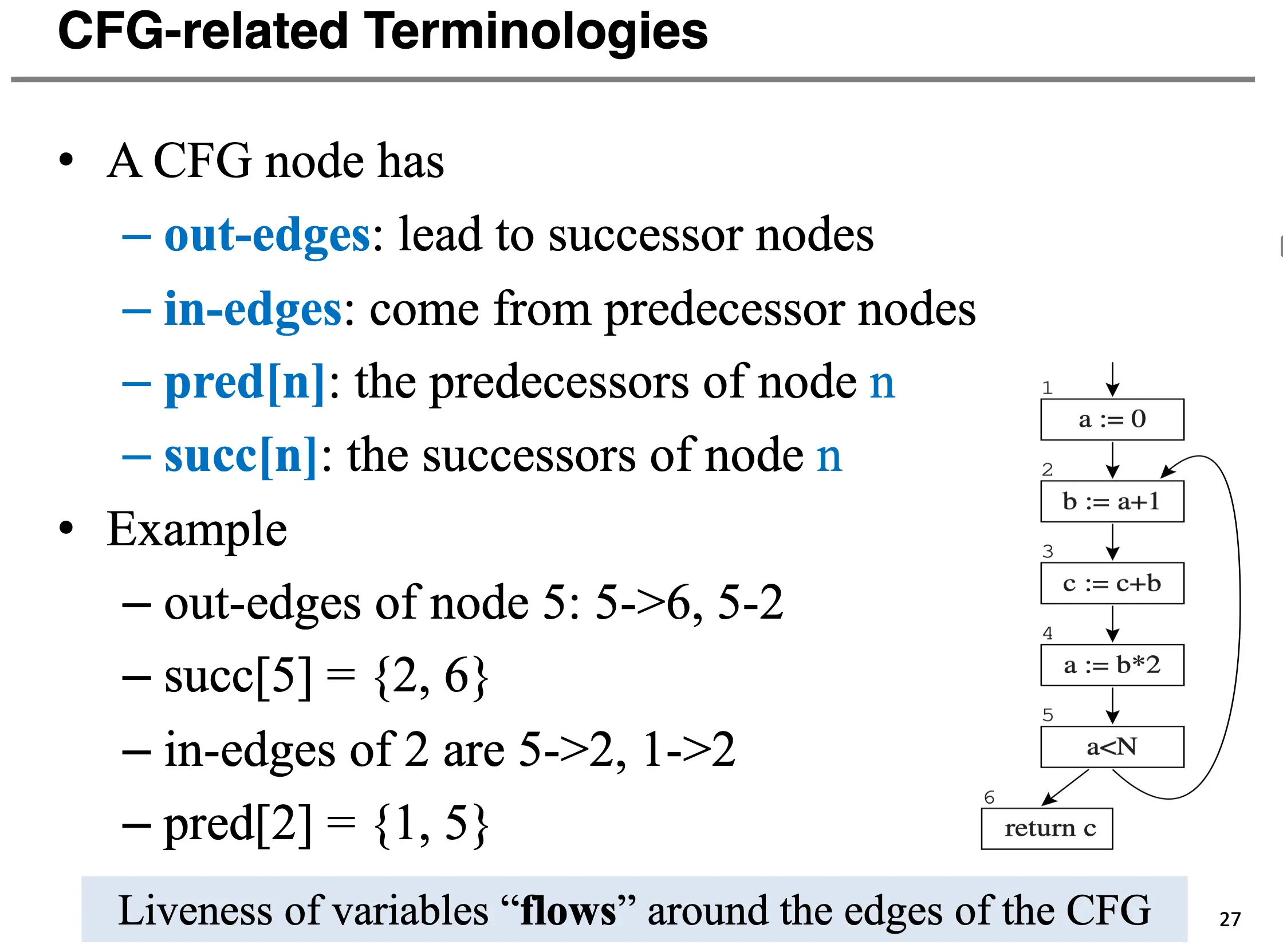
每一个 CFG 节点都有：

  • 出边/入边：来自前驱/后继节点的边；
  • 前驱 \(\operatorname*{pred}[n]\) 和后继 \(\operatorname*{succ}[n]\) 的集合；
  • 定义 \(\operatorname*{def}[n]\) 和使用 \(\operatorname*{use}[n]\) 的集合。
  • 入口活跃变量 \(\operatorname*{in}[n]\) 和出口活跃变量 \(\operatorname*{out}[n]\) 的集合。

活跃分析本质上就是求解入口活跃变量和出口活跃变量，后面会根据数据流方程和算法进行求解。

pred-succ

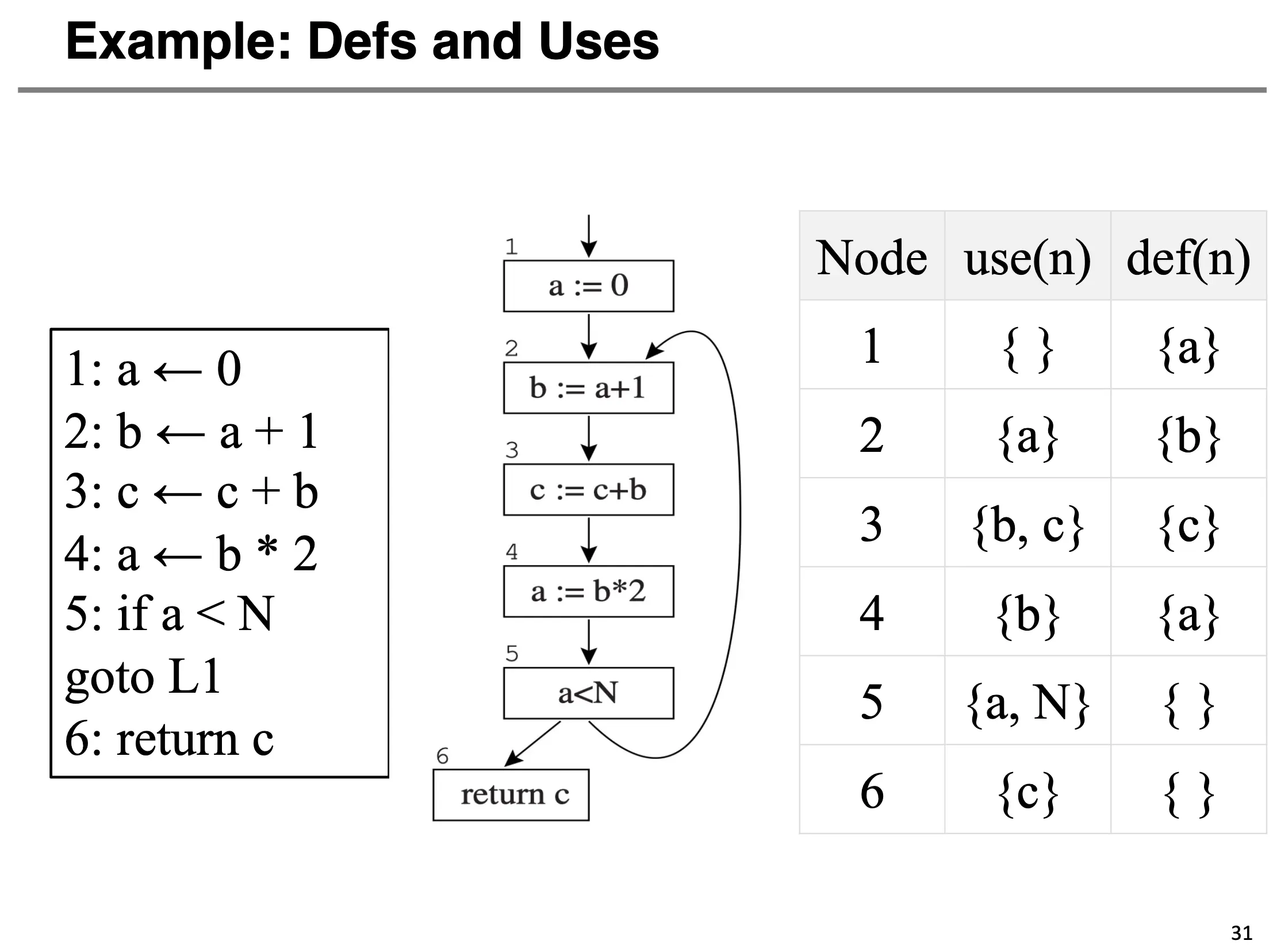
  • Def：对一个变量或者临时值进行赋值，\(\operatorname*{def}(n)\) 定义为在 n 处被定义的变量的集合；
  • Use：一个变量出现在了赋值语句的右侧或者别的表达式之中，\(\operatorname*{use}(n)\) 定义为在 n 处被使用的变量的集合。

def-use

活性事实/Liveness Facts：

  • 边上活跃/Live on an Edge：There is a directed path from that edge to a use of the variable that does not go through any def of the variable；
  • 入口活跃/Live-in：一个变量在一个节点处入口活跃，当其在这个节点的任何一个入边上活跃，\(\operatorname*{in}[n]\) 表示节点 n 的入口活跃变量集合；
  • 出口活跃/Live-out：一个变量在一个节点处出口活跃，当其在这个节点的任何一个出边上活跃，\(\operatorname*{out}[n]\) 表示节点 n 的出口活跃变量集合。

计算 \(\operatorname*{in}[n]\) 和 \(\operatorname*{out}[n]\)，有以下规则：

  • Rule 1：如果 \(a \in \operatorname*{in}[n]\)，则对于所有 \(m \in \operatorname*{pred}[n]\)，都有 \(a \in \operatorname*{out}[m]\)，换句话说，如果一个变量在节点 n 处入口活跃，那么其在所有 n 的前驱处都出口活跃；
  • Rule 2：如果 \(a \in \operatorname*{use}[n]\)，则 \(a \in \operatorname*{in}[n]\)，换句话说，如果一个变量在节点 n 处被使用，那么其在节点 n 处入口活跃；
  • Rule 3：如果 \(a \in \operatorname*{out}[n]\) 且 \(a \notin \operatorname*{def}[n]\)，则 \(a \in \operatorname*{in}[n]\)，换句话说，如果一个变量在节点 n 处出口活跃且没有被定义，那么其在节点 n 处入口活跃。

liveness-rule

因此我们可以导出下面两个方程:

\[\begin{aligned} \operatorname*{in}[n] &= \operatorname*{use}[n] \cup (\operatorname*{out}[n] - \operatorname*{def}[n]) \\ \operatorname*{out}[n] &= \bigcup_{m \in \operatorname*{succ}[n]} \operatorname*{in}[m] \end{aligned}\]

这意味着：

  • 在节点处使用的变量一定入口活跃（节点内部用到的变量必须在入口处可用）；
  • 在节点出口活跃且没有被重定义的变量一定是入口活跃的（节点不改写的出口活变量，要透传到入口）；
  • 在节点入口活跃的变量，其一定在其节点的后继节点出口活跃。

2.3 数据流方程的求解

算法分两步：

  • 将所有节点的 \(\operatorname*{in}[n]\) 和 \(\operatorname*{out}[n]\) 初始化为空集，直接可以从控制流图中看出来 \(\operatorname*{def}\) 集合和 \(\operatorname*{use}\) 集合；
  • 重复应用这两个方程，直到所有集合不再变化，即收敛，收敛之后输出；

liveness-algorithm

对于我们在上面举例 Def 和 Use 集合的 CFG，可以计算出最终的 \(\operatorname*{in}\) 和 \(\operatorname*{out}\) 集合如下：

liveness-result

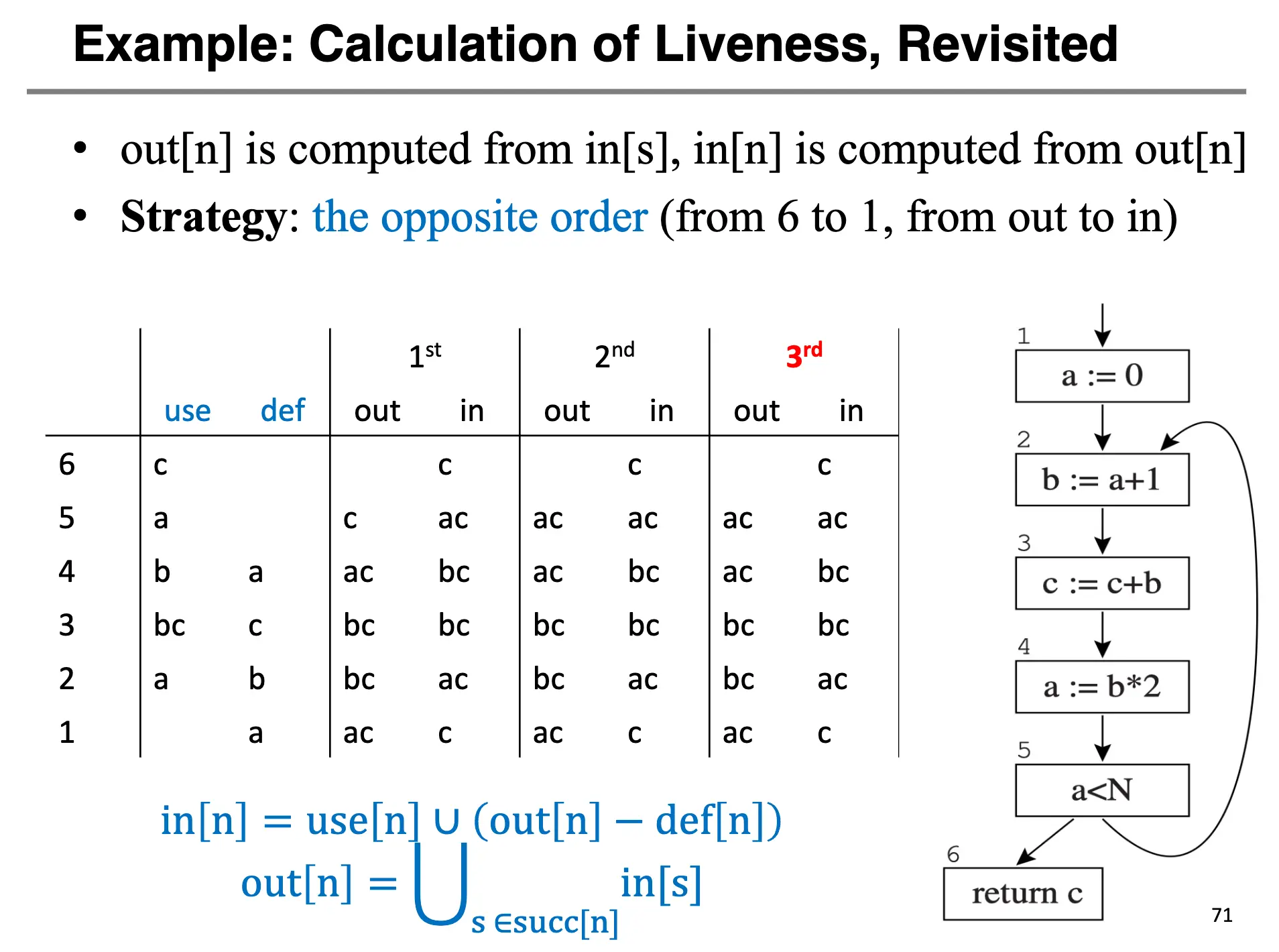
加速迭代的方法：观察到跨节点传递信息的规则只有 \(\operatorname*{out}[n] = \bigcup_{m \in \operatorname*{succ}[n]} \operatorname*{in}[m]\)，因此我们清楚，活性分析算法的本质其实就是反向分析，于是算法加入如下 patch：只需要记录每一个节点的后继如何变化，逆着控制流顺序更新节点，对每一个节点先计算 \(\operatorname*{out}[n]\)，再计算 \(\operatorname*{in}[n]\)。

liveness-speed

这样一来，只需要三次迭代即可收敛，而原来的算法需要七次迭代。

liveness-speed-2

3. 一些讨论

3.1 优化方法

  • 选择合适的遍历顺序；
  • 使用不同的 CFG，比如将多条只有一个前驱和后继的语句合并成一个节点，减少了节点和边的数目，加速数据流分析；
  • 修改集合表示方法，比如使用位向量表示或者排序链表表示，排序链表对于稀疏集合特别有效；
  • 按照变量分别进行活性分析，对于短寿命临时量特别高效；

3.2 理论结果

  • 对于大小为 \(N\) 的程序，至多有 \(N\) 个节点，\(N\) 个变量，因此每次集合操作最多占用 \(O(N)\) 时间；
  • 外层 Loop：每次操作至少引入一个新的活跃变量，一共有 \(O(N)\) 个变量，因此外层最多有 \(O(N^2)\) 次迭代；
  • 所有的 \(\operatorname*{in}\) 和 \(\operatorname*{out}\) 的集合大小加起来最多有 \(O(N^2)\) 个元素，因此每次集合操作最多占用 \(O(N^2)\) 时间；

因此最差情况的时间复杂度为 \(O(N^4)\)，但是实际中由于 proper ordering 和稀疏性，实际常介于 \(O(N)\) 到 \(O(N^2)\) 之间。

定理：活性方程通常有多组解，比如下面头两个就是解，但是第三个就不是解。

liveness-theorem

定理：活性方程存在一个最小不动点，且迭代算法必然收敛到这个最小不动点。