Topic 2：语法分析¶

约 7210 个字 20 行代码 22 张图片预计阅读时间 24 分钟

语法分析：分析程序的短语结构/Analysis the phrase structure of the program.

Outline

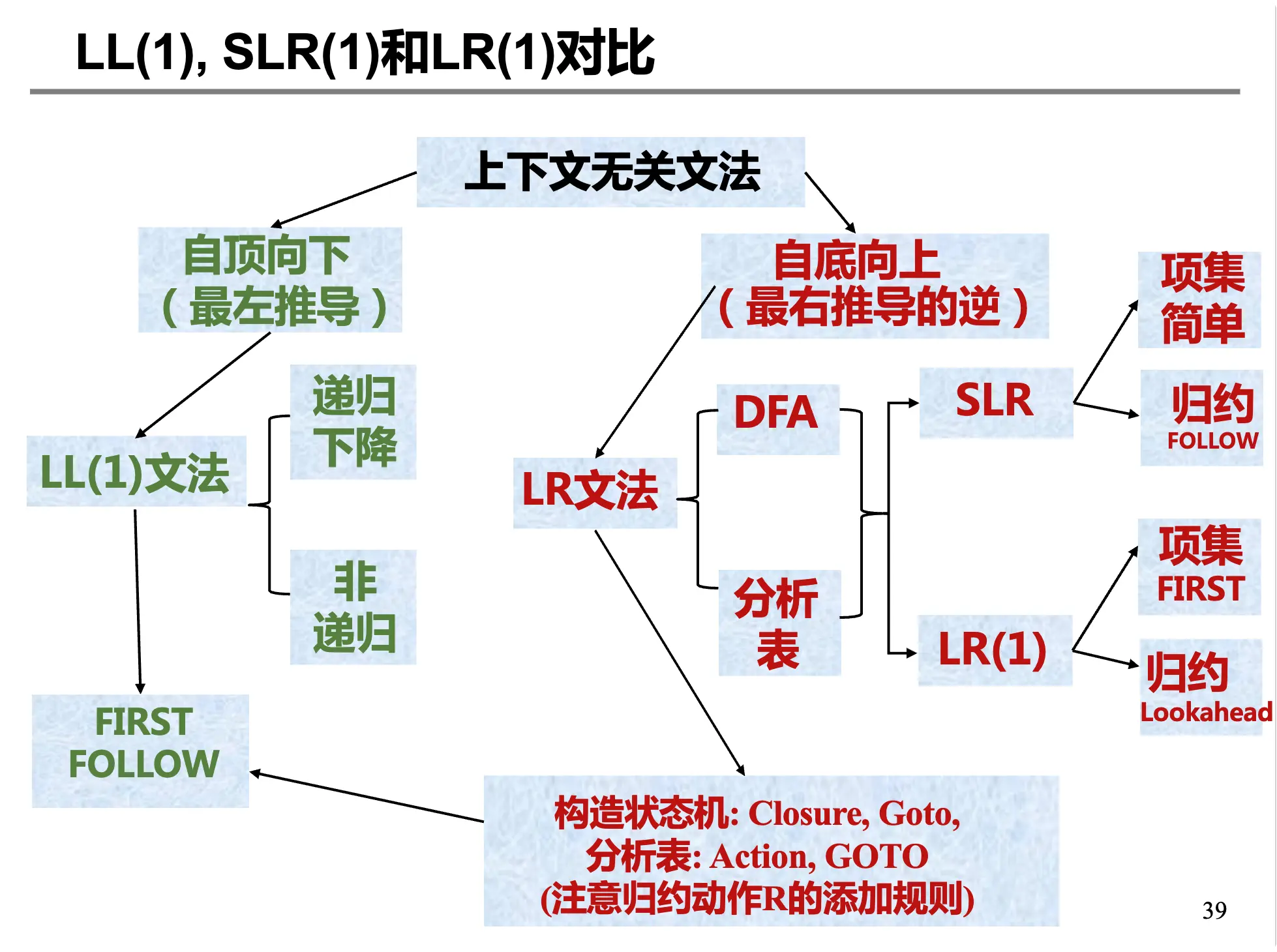
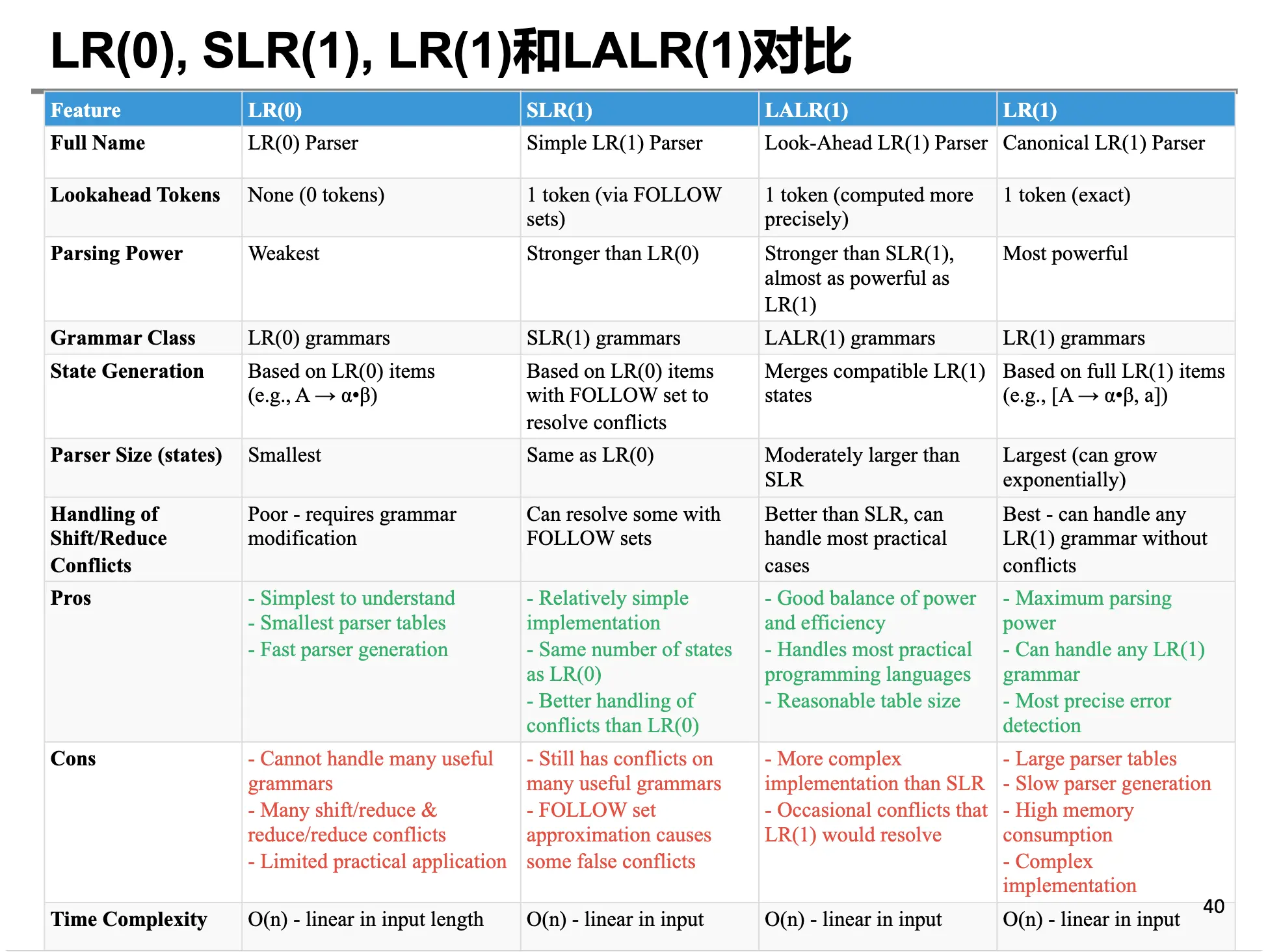
语法分析小结

1. 上下文无关文法¶

1.2 推导和规约¶

给定文法 $G = (T, N, P, S)$，定义直接推导、直接规约、多步推导、最左推导、最右推导如下：

直接推导：将产生式看成重写规则，将符号串中的非终结符用其产生式右侧的串代替。

如果 $A \rightarrow \gamma \in P$，且 $\alpha, \enspace \beta \in (T \cup N)^*$，则称 $\alpha A \beta$ 直接推导出 $\alpha \gamma \beta$，记作 $\alpha A \beta \Rightarrow \alpha \gamma \beta$。
直接规约：如果 $\alpha A \beta \Rightarrow \alpha \gamma \beta$，则称 $\alpha \gamma \beta$ 直接规约到 $\alpha A \beta$。
多步推导：如果 $\alpha_0 \Rightarrow \alpha_1 \Rightarrow \alpha_2 \Rightarrow$，$\cdots$，$\alpha_{n-1} \Rightarrow \alpha_n$，则称 $\alpha_0$ 经过 $n$ 步推导出 $\alpha_n$，记作 $\alpha_0 \Rightarrow^* \alpha_n$。

特别定义 $\Rightarrow^+$ 为经过正数步推导，$\Rightarrow^*$ 为经过若干（可以为 0）步的推导。
最左推导：在推导的每一步中，总是选择最左边的非终结符进行替换。在自顶向下的分析中，总是采用最左推导的方式。如果 $S \Rightarrow_{\text{lm}}^* \alpha_0$，则称 $\alpha_0$ 是当前文法的最左句型/Left-Sentential Form。
最右推导：在推导的每一步中，总是选择最右边的非终结符进行替换。
和最左推导和最右推导相反的分别是最右规约和最左规约，在自底向上的分析中，总是采用最左规约的方式。

定义句型，句子和语言如下：

句型/Sentential Form：对开始符号为 $S$ 的文法 $G$，如果 $S \Rightarrow^* \alpha$，则称 $\alpha$ 是 $G$ 的一个句型。

句型中可以包含终结符、非终结符，甚至可能是空串。
句子/Sentence：如果 $S \Rightarrow^* w$，$w \in T^*$，则称 $w$ 是 $G$ 的一个句子。

句子是不含非终结符的句型，仅含终结符号的句型是一个句子。
语言/Language：由文法 $G$ 推导出的所有句子构成的集合，记为 $L(G)$。

\[L(G) = \left\{ w \mid S \Rightarrow^* w, w \in T^* \right\}\]

上下文无关：对于形如 $\alpha A \beta \Rightarrow \alpha \gamma \beta$ 的推导，$A \rightarrow \gamma$ 是文法的一个产生式，在文法推导的每一步，符号串 $\gamma$ 仅仅根据 $A$ 的产生式推导，并不需要依赖 $A$ 的上下文 $\alpha$ 和 $\beta$。

问题：给定文法，如何判定输入串属于文法规定的语言？

从生成语言的角度：如果从开始符号可以推导出输入串，则输入串属于文法规定的语言；
从识别语言的角度：如果输入串可以规约到开始符号，则输入串属于文法规定的语言。

1.3 分析树/Parse Tree¶

分析树的性质：

分析树的根节点为开始符号 $S$；
每个内部节点是一个非终结符；
每个叶子节点是一个终结符；
每个父节点和其子节点构成一条产生式。

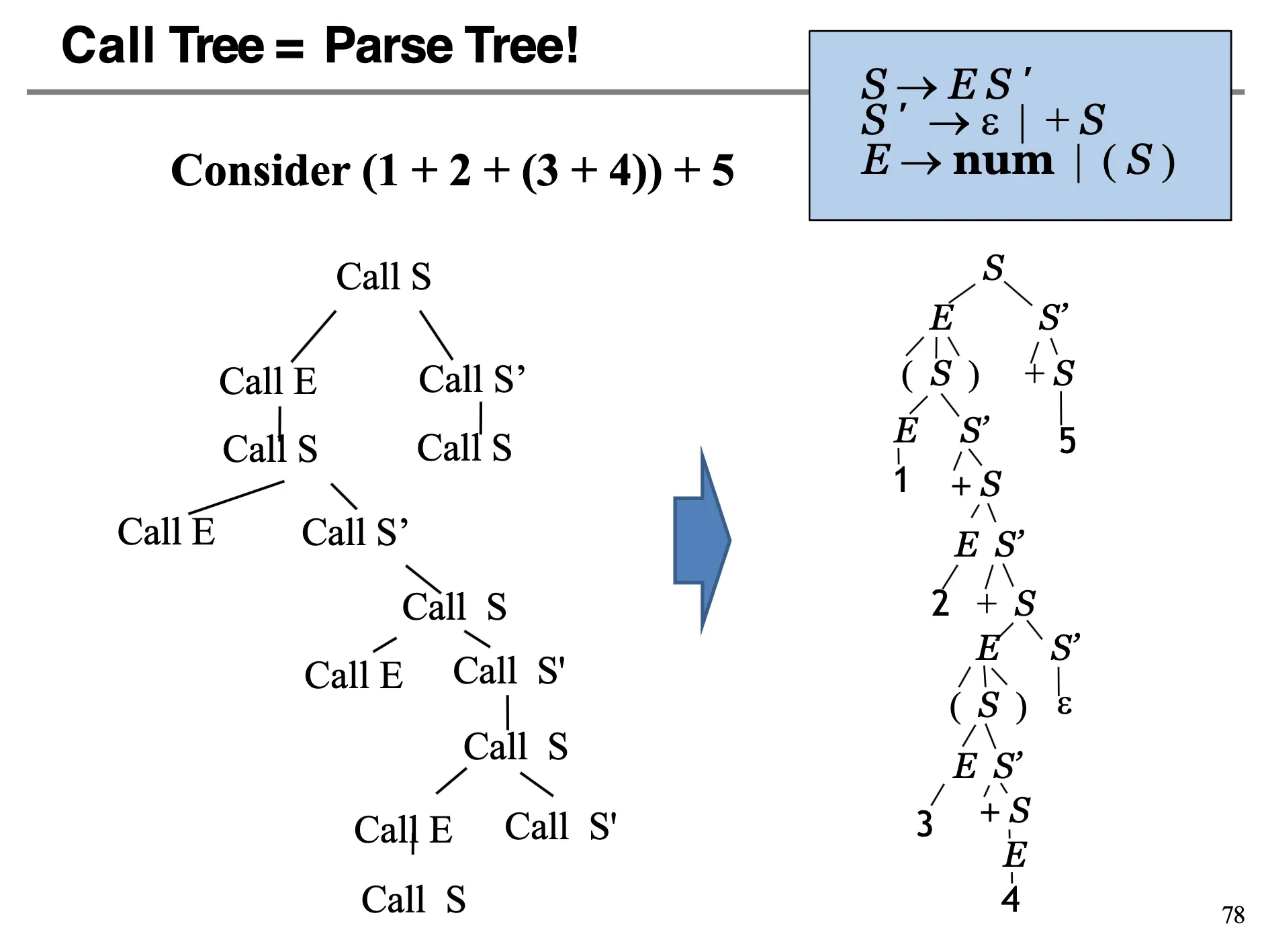
下面可以对给定的串构造一个 Parse Tree：

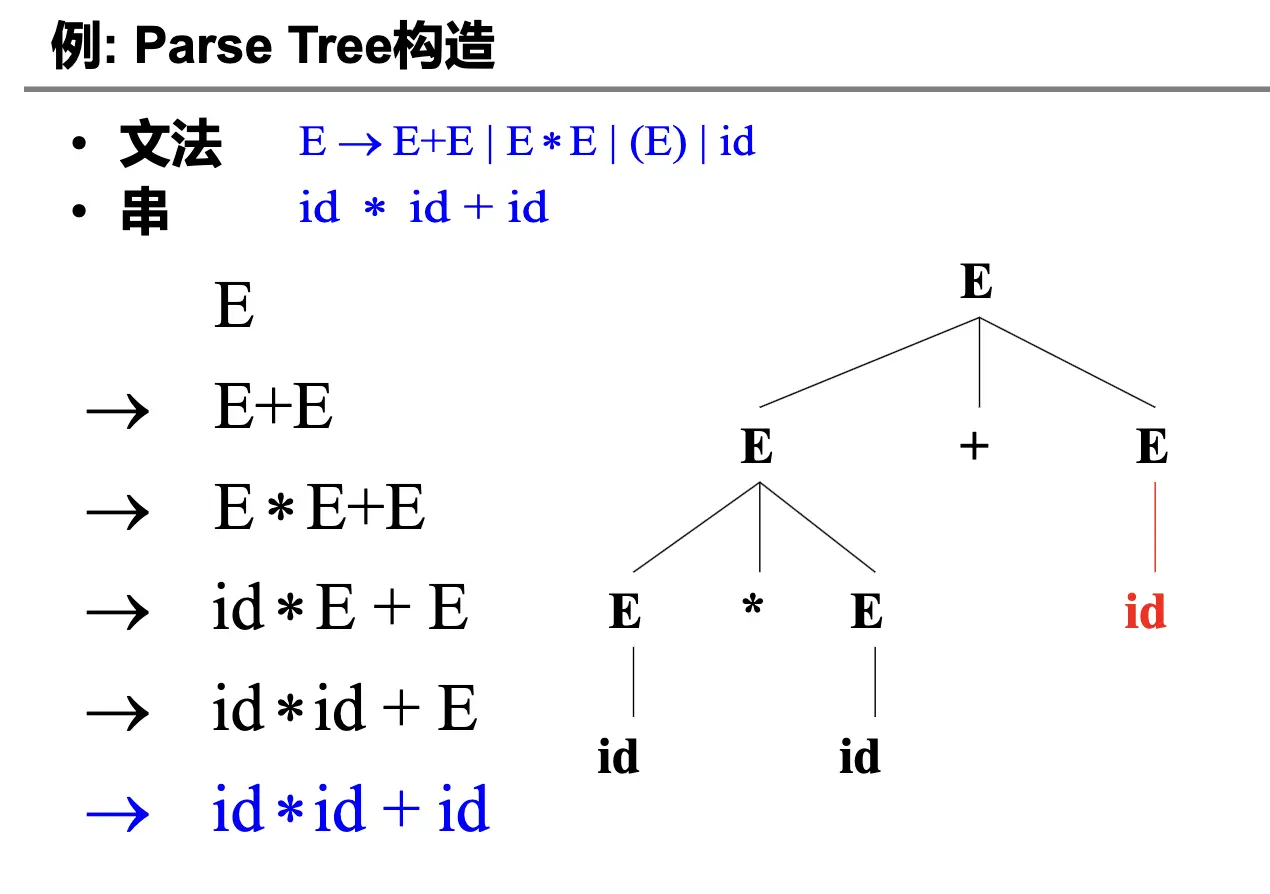
对于一般的上下文无关文法，parse 其一般需要 $O(n^3)$ 的时间复杂度（Universal Parsing）。但是对某些上下文无关的语言，只需要 $O(n)$ 的时间复杂度:

使用 LL(1) 文法的预测分析（自顶向下分析）；
使用 LR(1) 文法的 Shift-Reduce 分析（自底向上分析）。

2. 设计编程语言的文法¶

二义性文法/Ambiguous Grammar：如果一个文法的某些句子存在不止一棵分析树，则称该文法是二义的。或者说，若一个文法中存在某些句子，其有两个不同的最左/最右推导，那么这个文法是二义性的。

程序设计语言的文法应该都是无二义性的。否则就会导致一个程序有多重符合文法的解释。但是给定 CFG 文法，判定其是否具有二义性是一个不可判定问题。

比如：文法 $E \rightarrow E + E \mid E * E \mid (E) \mid id$ 是二义的，因为句子 $id + id * id$ 有两个不同的最左推导。其根源是多种正确推导处在文法同一层。

二义性文法的消除：惯用技术是分层：规定符号的优先级和结合性。

运算优先级：根据运算符不同的优先级，引入新的非终结符，其中越靠近开始符号的非终结符优先级越低；
运算结合性：递归非终结符在终结符左边，运算就左结合。

比如之前的文法可以修改为：

\[\begin{aligned} E &\rightarrow E + T \mid T \\ T &\rightarrow T * F \mid F \\ F &\rightarrow (E) \mid id \end{aligned}\]

悬空 else：

3. 递归向下分析¶

自顶向下分析：从文法的开始符号出发，尝试推导出输入串，分析树从根部开始构造，并且总是选择最左非终结符进行替换（从上到下，从左到右）。

剩下的唯一问题就是我们在每一步究竟应该选择哪个产生式进行替换。

递归向下分析/Recursive Descent Parsing：

由一组过程/函数组成，每一个过程对应一个非终结符；
从开始符号 $S$ 对应的过程开始，递归调用别的过程；
如果 $S$ 对应的过程恰好扫描了整个输入串，则分析成功。

对于利用非终结符 $A$ 的文法规则 $A \rightarrow X_1 \ldots X_k$，定义识别 $A$ 的过程：

如果 $X_i$ 是终结符，匹配输入串中对应的终结符 $a$：如果终结符不同或者没有下一个输入，说明发生了错误，需要回溯；
如果 $X_i$ 是另一个非终结符，则递归调用识别 $X_i$ 的过程：

尝试第一个从该非终结符引出的产生式，即将该产生式的右端作为该结点的子结点加入 Parse Tree，然后依次遍历子结点；

如果回溯到了当前非终结符，则尝试下一个产生式；

如果回溯到了当前非终结符但所有产生式都已经尝试完了，那么说明该非终结符是不应当出现的，回溯到上一步非终结符。
如果选择了不合适的产生式，那么可能需要回溯，过程如上述。

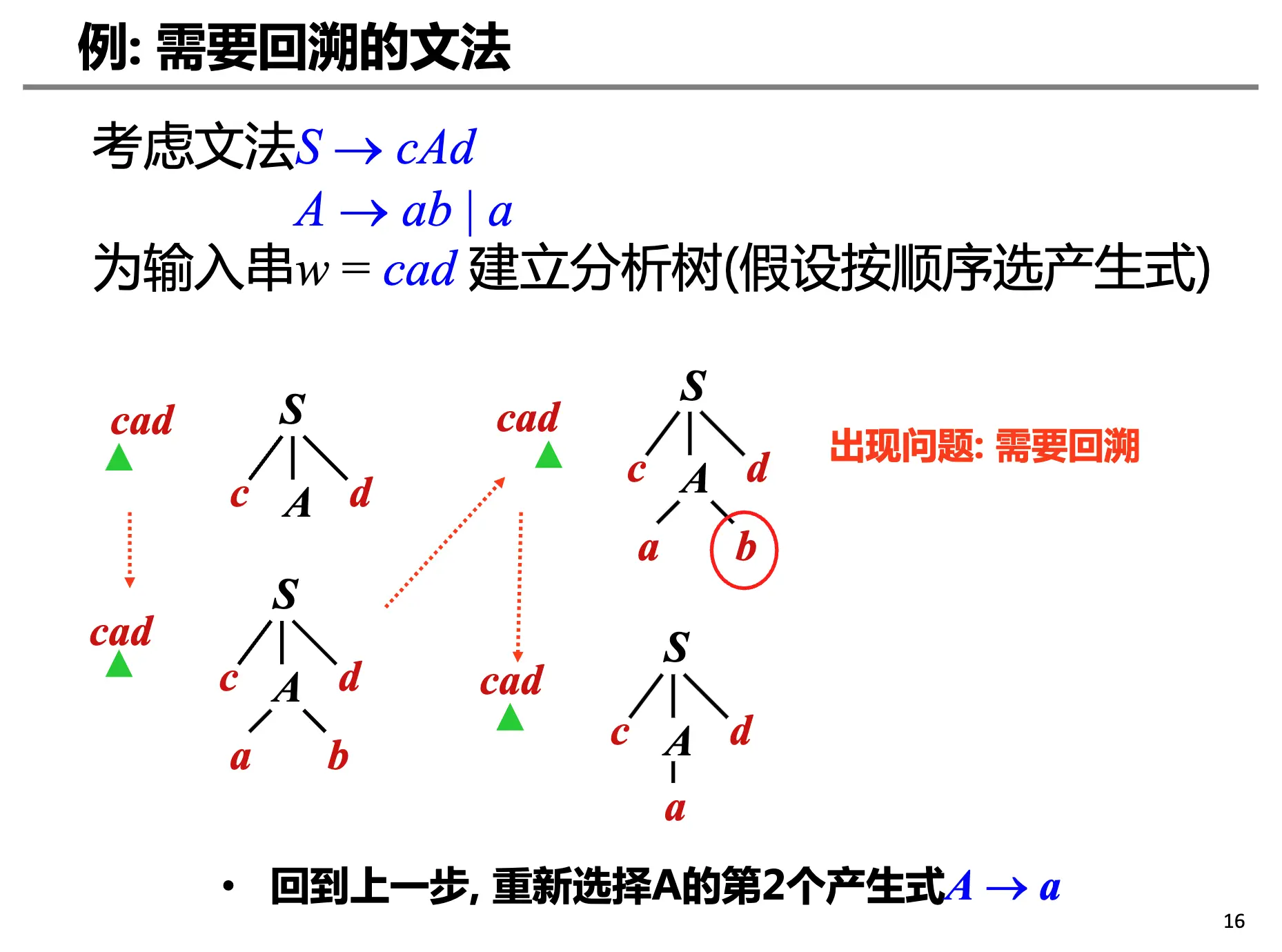
问题在于复杂的回溯的代价太高，分析过程类似于 NFA，因此我们希望构建一个类似于 DFA 的分析方法。这样就产生了接受 LL(k) 文法的预测分析法/Predictive Parsing。其中 LL(k) 表示从左到右分析，最左推导，向前看 k 个 Token 来确定产生式。并且我们需要确定文法加上什么限制可以保证没有回溯。

4. LL(1) 和预测分析¶

4.1 First 集和 Follow 集¶

给定文法 $G = (T, N, P, S)$，对于 $\alpha \in (T \cup N)^*$，$A\in N$，定义 $\alpha$ 的 First 集和 $A$ 的 Follow 集如下：

$\operatorname*{First}(\alpha)$：可以从 $\alpha$ 推导得到的串的首个终结符的集合。

也就是 $\operatorname*{First}(\alpha) = \left\{ a \mid \alpha \Rightarrow^* a \beta, a \in T, \beta \in (T \cup N)^* \right\}$；
$\operatorname*{Follow}(A)$：从 $S$ 出发，可能在推导过程中直接跟在 $A$ 后边的终结符的集合。

也就是 $\operatorname*{Follow}(A) = \left\{ a \mid S \Rightarrow^* \beta A a \gamma, a \in T, \beta, \gamma \in (T \cup N)^* \right\}$；

由于 First 集和 Follow 集都涉及到空串，因此需要考虑可以推导出空串的 Nullable 符号：

$\operatorname*{Nullable}(A)$：可以推导出空串的非终结符的集合，使用递归方法形式化定义：
Base Case：$X \rightarrow \varepsilon$，则 $X$ 一定是 Nullable 的；
Inductive Case：如果 $X \rightarrow Y_1 \ldots Y_k$ 是一个产生式，且 $Y_1, \ldots, Y_k$ 都是可以推导出空串的非终结符，则 $X$ 也是 Nullable 的。

类似可以归纳定义 First 集和 Follow 集，这也是计算 First 集和 Follow 集的算法：

First 集：

Base Case：如果 $X$ 是一个终结符，则 $\operatorname*{First}(X) = \{X\}$；
Inductive Case：如果 $X \rightarrow Y_1 \ldots Y_k$ 是一个产生式：
- $\operatorname*{First}(X) \leftarrow \operatorname*{First}(Y_1) \cup \operatorname*{First}(X)$；
- 如果 $Y_1 \in \operatorname*{Nullable}$，则 $\operatorname*{First}(X) \leftarrow \operatorname*{First}(X) \cup \operatorname*{First}(Y_2)$；
- 如果 $Y_1, \ldots, Y_{k-1} \in \operatorname*{Nullable}$，则 $\operatorname*{First}(X) \leftarrow \operatorname*{First}(X) \cup \operatorname*{First}(Y_k)$；

Follow 集：

Base Case：$\operatorname*{Follow}(A) = \{\}$。
Inductive Case：如果 $B \rightarrow s_1 A s_2$ 是一个产生式
- $\operatorname*{Follow}(A) \leftarrow \operatorname*{Follow}(A) \cup \operatorname*{First}(s_2)$。
- 如果 $s_2 \in \operatorname*{Nullable}$，则 $\operatorname*{Follow}(A) \leftarrow \operatorname*{Follow}(A) \cup \operatorname*{Follow}(B)$。

对于归纳的第二种情况，假设 $S \Rightarrow^* \ldots B b \ldots$，其中 $b \in \operatorname*{Follow}(B)$，那么使用 $B \rightarrow s_1 A s_2$ 推导出 $S \Rightarrow^* \ldots s_1 A s_2 b \ldots$，其中 $b \in \operatorname*{First}(s_2)$，因此 $b \in \operatorname*{Follow}(A)$。

PPT 上的例子

三个集合事实上可以同时计算（虎书 Alg 3.13）：

4.2 LL(1) 文法¶

LL(1) 文法：该文法的任意两个产生式 $A \rightarrow \alpha \mid \beta$ 都满足下面条件：

$\alpha$ 和 $\beta$ 都推导不出以同一个单词为首的串：$\operatorname*{First}(\alpha) \cap \operatorname*{First}(\beta) = \varnothing$；
$\alpha$ 和 $\beta$ 中至多有一个可以推导出空串，且如果 $\beta$ 可以推导出空串，则 $\operatorname*{First}(\alpha)$ 不应该在 $\operatorname*{Follow}(A)$ 中：$\operatorname*{First}(\alpha) \cap \operatorname*{Follow}(A) = \varnothing$。

这样就可以保证产生式选择的唯一性。假设下一个输入是 $b$：

如果两个产生式的右侧都不产生空串，如果 $b \in \operatorname*{First}(\alpha)$，则选择 $\alpha$ 对应的产生式，反之选择 $\beta$ 对应的产生式；
如果 $\beta$ 可以推出空串，则如果 $b \in \operatorname*{First}(\alpha)$，则选择 $\alpha$ 对应的产生式，反之如果 $b \in \operatorname*{Follow}(A)$，则选择 $\beta$ 对应的产生式，这对应着 $A$ 最后通过 $\beta$ 到达了 $\varepsilon$ 且 $A$ 的后面跟着 $b$ 的情况。

4.3 预测分析的实现：预测分析表¶

预测分析表：

行 $A$：对应一个非终结符；
列 $a$：对应一个终结符或者输入结束符 $$ $；
表项 $\mathrm{M}[A, a]$：针对非终结符 $A$，下一个输入 Token 为 $a$ 的时候可选的产生式。

构造预测分析表的算法如下：对文法 $G$ 的每个产生式 $A \rightarrow \gamma$，执行如下操作：

如果 $t \in \operatorname*{First}(\gamma)$，则将 $A \rightarrow \gamma$ 加入 $\mathrm{M}[A, t]$；
如果 $\gamma$ 是 Nullable 的，且 $t \in \operatorname*{Follow}(A)$，则将 $A \rightarrow \gamma$ 加入 $\mathrm{M}[A, t]$。

如果某一个表项为空，那么以为这当前非终结符的下一个输入绝对不能是该表项对应的终结符。输入的串语法错误。

通过预测表可以定义 LL(k) 文法:

如果每一个列只对应一个终结符，并且产生的预测分析表的每一个表项都不含有多重的产生式，那么该文法是 LL(1) 文法。
如果每一个列对应着多个终结符链接的串，每一个串长度为 $k$，并且产生的预测分析表的每一个表项都不含有多重的产生式，那么该文法是 LL(k) 文法。

任何有二义性的文法都不是 LL(k) 文法。

4.4 预测分析的实现：递归下降预测分析¶

直接看对于这个文法的实现就可以：

形式化算法形如（这个是另一个文法的算法了，并且这个文法有左递归，因此不是 LL(1) 文法）：

void S(void) { E(); eat(EOF); } 
void E(void) {
    switch(tok) { 
        case ?: E(); eat(PLUS); T(); break;
        case ?: E(); eat(MINUS); T(); break;
        case ?: T(); break; 
        default: error();
    }
}

4.5 LL(1) 预测分析的非递归实现¶

主要想法是使用一个显式的栈，而不是递归调用完成分析。使用类似模拟 LL 文法对应的 Pushdown Automata 的方式完成分析。

如果栈顶式非终结符 $A$，利用预测分析表，选择产生式 $A \rightarrow \gamma$，将 $\gamma$ 逆序压入栈中；
如果栈顶式终结符 $a$，则将栈顶记号 $a$ 和输入中的 Token 相匹配。
初态：压入初始符号；终态：栈为空，此时接受。

4.6 文法改造：提左公因子¶

LL(1) 文法有三个重要的性质：无二义、无左公因子、无左递归。

有左公因子/Left-factored 的文法：$P \rightarrow \alpha \beta \mid \alpha \gamma$。其问题在于同一个非终结符的多个候选式存在共同前缀，很可能导致回溯，因为其 First 集的交集不为空。解决思路是限制文法或者进行文法变换。

提左公因子：首先定义 $Q \rightarrow \beta \mid \gamma$，则 $P \rightarrow \alpha Q$。也就是通过改写产生式来延迟决定，等读入足够多的信息之后再做选择。

4.7 文法改造：消除左递归¶

左递归/Left-recursive 文法：如果一个文法中有非终结符号 $A$ 使得 $A \Rightarrow^+ A \alpha$，则称该文法是左递归的。比如 $A \rightarrow A \alpha \mid \beta$，这称为直接/立即左递归。

问题在于递归下降分析可能进入无限循环，比如考虑串 $\beta \alpha^n$，最左推导可能产生 $A \Rightarrow \cdots \Rightarrow A \alpha^n$。

对于直接左递归，解决方法是将左递归转化成右递归：观察到 $A$ 生成的串以某个 $\beta$ 开头，后面有若干个 $\alpha$，则可以改写文法为 $A \rightarrow \beta A^{\prime}$，$A^{\prime} = \alpha A^{\prime} \mid \varepsilon$。

上述方法解决的是消除直接左递归的方法，对于两步或者多步推导产生的左递归，可以参考龙书中介绍的方法：

4.8 错误恢复¶

编译器的错误处理：

词法错误：如标识符、关键字或者算符的拼写错误；
语法错误：如算数表达式的括号没配对；
语义错误：如算符作用于不相容的运算对象；
...

错误处理的基本目标：

清楚而准确地报告错误的出现，并且尽量少伪错误；
迅速从错误中恢复出来，以便诊断后面的错误；
不应该使正确程序的处理速度降低太多。

在语法分析中，由于访问空的预测分析表标明了语法错误，一个程序可能有多种错误，下面是可能的解决方法：

抛出异常并且终止解析：不鲁棒也不用户友好，用户需要解决当前的错误才能继续编译，发现下一个错误；
插入标记法：假装我们有了期望的标记，并且正常返回，但是问题在于可能不会终止，如果遇到严重的语法错误，解析器可能无法恢复，导致无限循环，插入的标记也可能造成后续更加严重的语法错误；

删除标记法：维护每一个非终结符的 Follow 集合，当遇见语法错误的时候，Parser 跳过输入标记，直到找到 Follow 集中的 Token 为止。这种方法更加安全，因为循环一定会遇到 EOF 的时候截止。并且可以在一次解析的时候发现更多错误。

int Tprime_follow[] = {PLUS, RPAREN, EOF};
void Tprime() {
switch (tok) {
    case PLUS: break;
    case TIMES: eat(TIMES); F(); Tprime(); break;
    case RPAREN: break;
    case EOF: break;
    default: print("expected +, *, right-paren, or end-of-file");
             skipto(Tprime_follow);
    }
}

5. Shift-Reduce¶

回忆：自底向上分析，从串 $w$ 规约为文法开始符号 $S$。核心的问题有两个：

何时规约，规约为哪些符号串？
规约到哪个非终结符号？

Shift-Reduce 的想法是：将输入串分割成两个子串 $\alpha \mid \beta$，其中我们使用分隔符 $\mid$ 标记分割的点：

右侧子串：仅仅包含一系列终结符，为没有被 Parser 分析的部分；
左侧子串：为一系列终结符和非终结符，为已经被 Parser 分析的部分。
在最初的时候，所有输入都在右侧子串 $\mid x_1 x_2 \ldots x_n$，左侧子串为空。

例子如下：

\

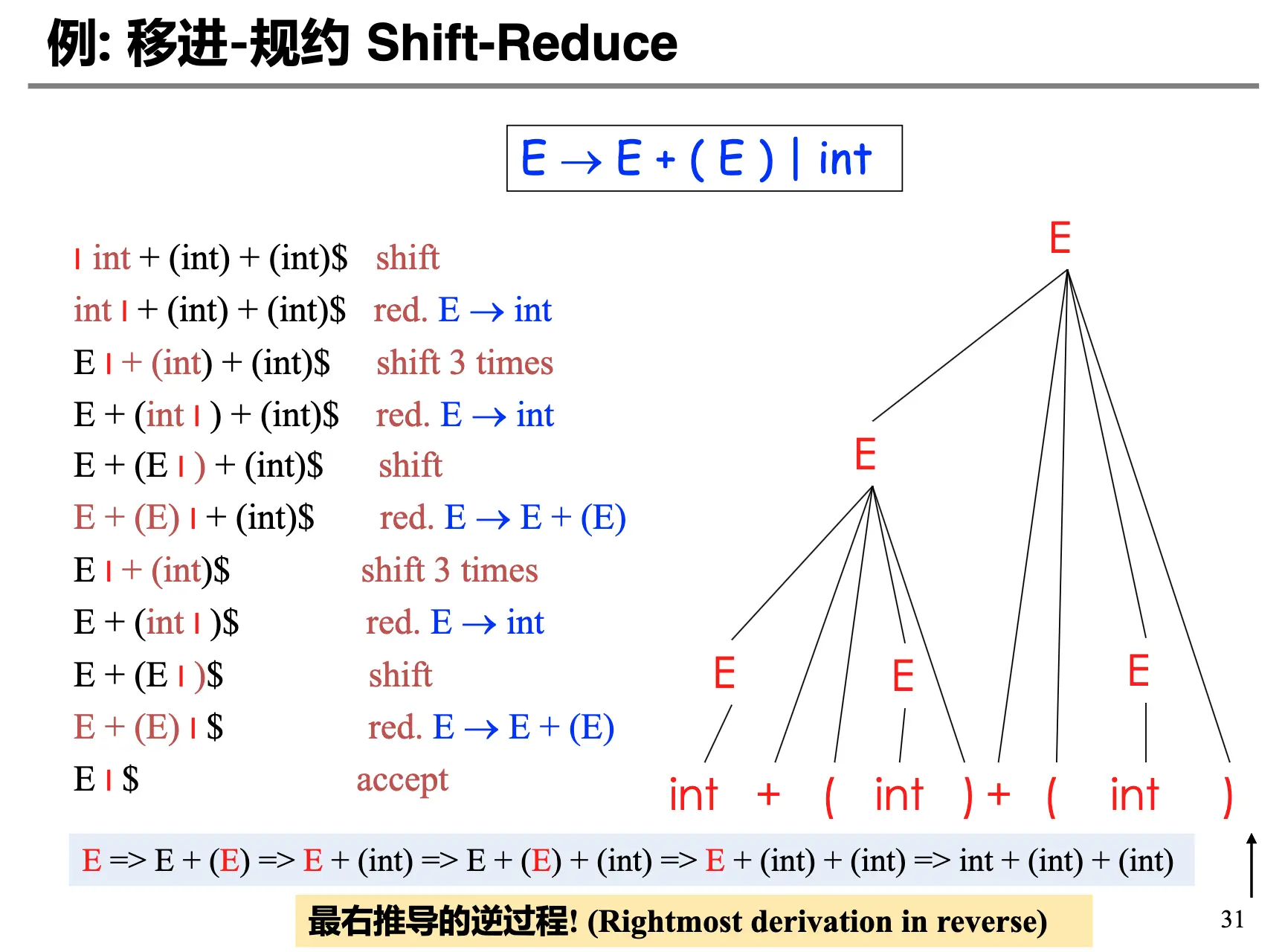LR 分析有两个关键组件：

符号栈/Symbol Stack：存储左侧子串（包含终结符和非终结符）；
输入流/Input Stream：存储剩余的输入（右侧子串，包含终结符）；
后面还会提到状态栈/State Stack。

LR 分析的四种操作：

移进/Shift：将下一个输入（终结符）压入符号栈的栈顶；
规约/Reduce：栈顶应该匹配某个规则的右侧，弹出对应规则对应的符号，将规则左侧压入栈顶；
错误/Error：当无法执行移进或规约时，发生错误。
接受/Accept：移进 EOF 并且可以将栈中的剩余内容规约到起始符号。

6. LR(0) 分析¶

6.1 LR(0) Parsing NFA¶

首先需要注意的是，这里的 NFA 并不是用来识别 LR(0) 语言的自动机，NFA 仅仅可以用来识别正则语言，但是 LR(0) 语言是上下文无关语言，这个 NFA 是用来记录当前识别进度的自动机，帮助判断栈顶内容是否可以规约。

想法：由于自底向上分析的过程是不断凑出产生式的 RHS 的过程，假设下一次将要用到的产生式为 $A \rightarrow \alpha \beta$，那么进行规约之前，栈顶有可能包含三种情况：$\ldots$，$\ldots \alpha \ldots$，$\ldots \alpha \beta \ldots$。根据凑出这个产生式 RHS 的进度不同，我们希望对其进行不同的操作，而关键问题是我们如何知道栈顶的内容是可以规约的，这就恰好激发我们维护一个记录当前识别的进度的状态的想法。

项/Item：一个产生式加上在其中某处的一个点，比如对于产生式 $A \rightarrow \alpha \beta$，其有三个 Item：$A \rightarrow \cdot \alpha \beta$，$A \rightarrow \alpha \cdot \beta$，$A \rightarrow \alpha \beta \cdot$。有不同的含义：

$A \rightarrow \alpha \cdot \beta$：已经扫描/规约了 $\alpha$，并且希望接下来的输入中经过扫描/规约得到 $\beta$，然后将 $\alpha \beta$ 规约成 $A$；
$A \rightarrow \alpha \beta \cdot$：已经扫描/规约得到了 $\alpha \beta$，可以把 $\alpha \beta$ 规约到 $A$。

状态跳转：一个项读入一个符号之后就可以转变为另外一个项：比如 $A \rightarrow \alpha \cdot \beta$ 读入符号 $\beta$ 之后就变成了 $A \rightarrow \alpha \beta \cdot$。

而恰好，一个项的集合加上状态跳转的规则，恰好可以构成一个 NFA，并且项的数量是有限的（这是因为文法产生式是有限的，并且每个产生式右侧的长度也是有限的），对应的自动机称之为 LR(0) 自动机。

LR 分析器基于状态来构造自动机进行 RHS 的识别。相对于一般的 NFA 添加的内容如下：

起始 & 终结状态：在文法中添加新的开始符号 $S^{\prime}$，并且 $S^{\prime} \rightarrow S \$ \(，$S\) 是文法的开始符号，$$ $ 是输入结束符。
状态迁移关系：
- $X \rightarrow \cdot \alpha \beta$ 在接受输入 $\alpha$ 之后会变成 $X \rightarrow \alpha \cdot \beta$。
- 如果存在产生式 $X \rightarrow \alpha Y \beta$，并且 $Y$ 是一个非终结符且有产生式 $Y \rightarrow \gamma$，则 $X \rightarrow \alpha \cdot Y \beta$ 可以转换到 $Y \rightarrow \cdot \gamma$。（这是因为希望看到由 $Y \beta$ 推导出的串，首先要看到 $Y$ 推导出的串，因此加上 $Y$ 各个产生式对应的项）

因此可以构造出这样的 NFA：

6.2 LR(0) Parsing DFA¶

LR(0) 分析的核心是构造一个特殊的 DFA，这个 DFA 的每一个状态是一组 LR(0) 项（我们称为项集），通过之前构造的 NFA 可以构造出这个 DFA。

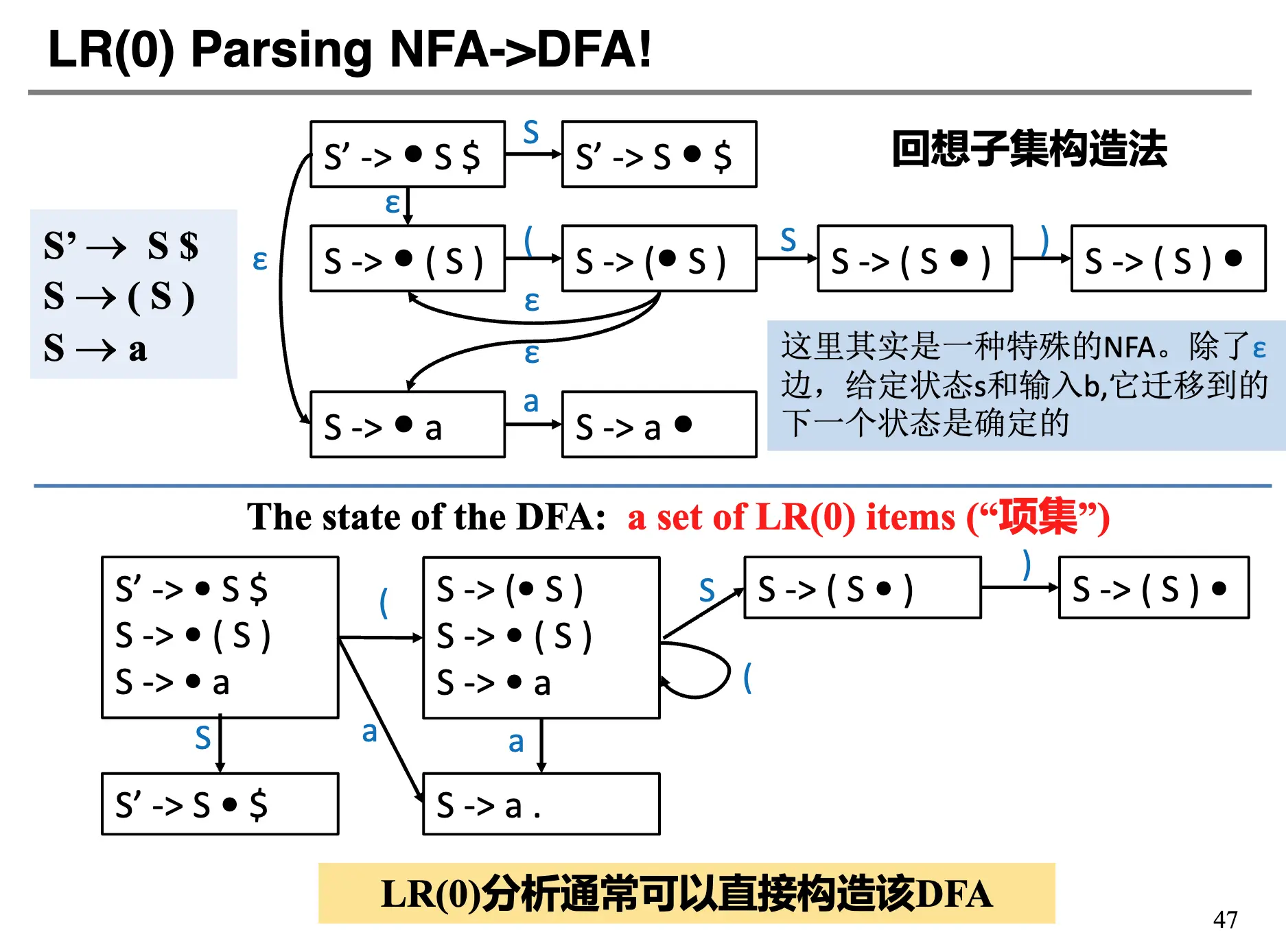
但是对于 LR 分析家族，我们一般是直接构造 DFA。构造过程依赖于 Closure 函数和 Goto 函数以及收敛条件：

$I$：A Set of Items，$X$：A Symbol (Terminal or Non-Terminal)，$T$：A Set of States；$E$：The set of (Shift or Goto) edges；
$\operatorname*{Closure}(I)$：实际上是计算 $I$ 的 $\varepsilon$ 闭包：
- 对于 $I$ 内的任意一个项 $A \rightarrow \alpha \cdot X \beta$，如果 $X$ 是一个非终结符，且有一个产生式 $X \rightarrow \gamma$，则将 $X \rightarrow \cdot \gamma$ 加入 $I$；
- 重复上述过程直到 $I$ 不再变化，返回 $I$。
$\operatorname*{Goto}(I, X)$：计算 $I$ 在 $X$ 下的转移：
- 定义为 $I$ 中所有形如 $A \rightarrow \alpha \cdot X \beta$ 的项所对应的项 $A \rightarrow \alpha X \cdot \beta$ 的集合的闭包；
- 初始化 $J$ 为空集；
- 对于 $I$ 中的任意一个项 $A \rightarrow \alpha \cdot X \beta$，将 $A \rightarrow \alpha X \cdot \beta$ 加入 $J$；
- 返回 $\operatorname*{Closure}(J)$。
收敛条件：
- 将 $T$ 初始化为 $\{\operatorname*{Closure}(\{S^{\prime} \rightarrow \cdot S\$ \})\}$，将 $E$ 初始化为空集；
- 对 $T$ 的每一个状态 $I$，对 $I$ 的每一个项 $A \rightarrow \alpha \cdot X \beta$，计算 $\operatorname*{Goto}(I, X)$，如果结果为 $J$，则令 $T \leftarrow T \cup \{J\}$，并且令 $E \leftarrow E \cup \{I \overset{X}{\rightarrow} J\}$；
- 重复上述过程直到 $T$ 和 $E$ 不再变化。

完整算法如下：

6.3 构造 LR(0) 分析表¶

和 LL(1) 的预测分析表一样，LR(0) 分析表指导我们对于每一个状态和输入的符号，该执行什么操作。假设我们已经有了 LR(0) Parsing DFA，那么我们可以构造出 LR(0) 分析表。

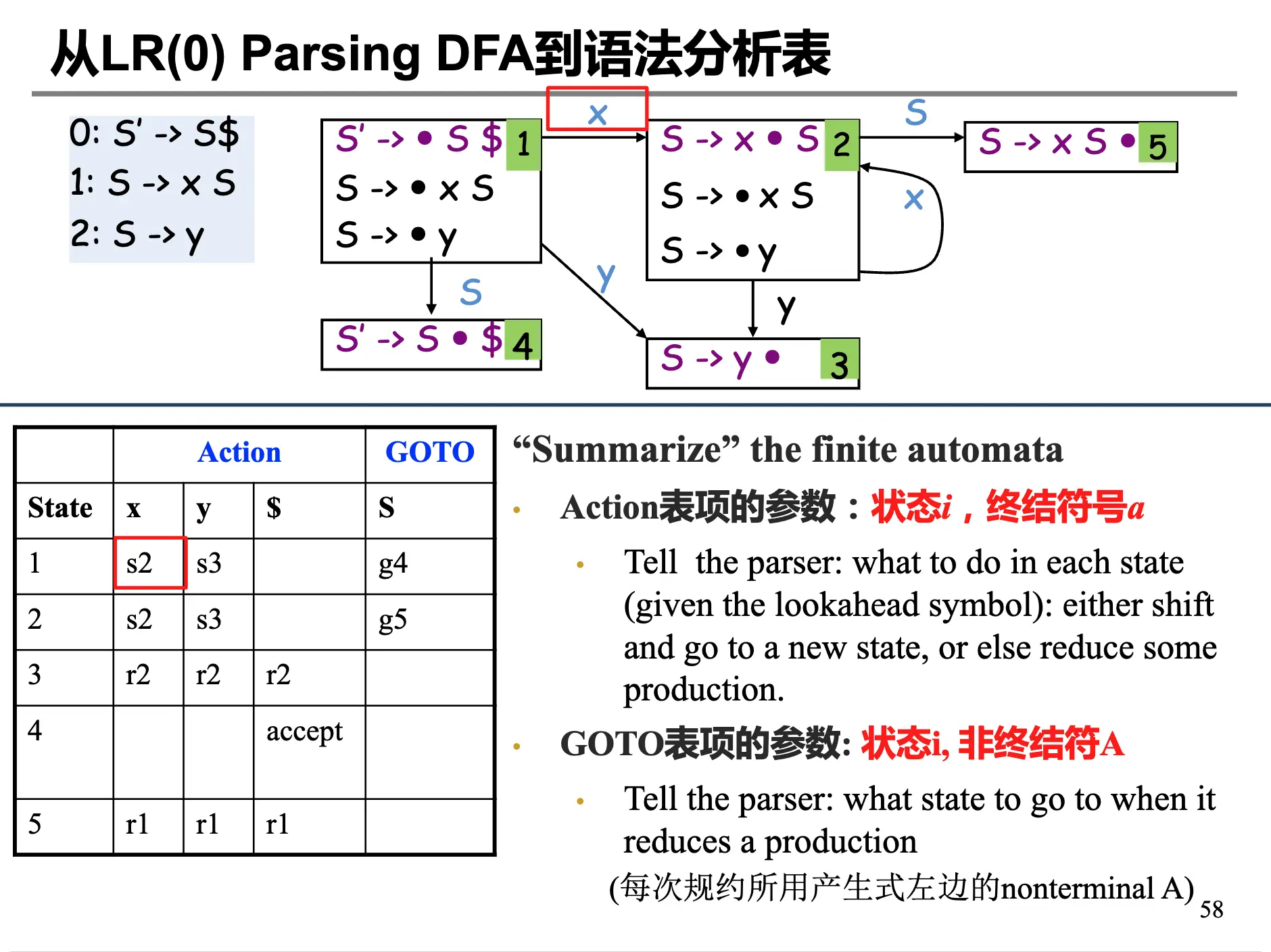
注意这里的 GOTO 表项的参数为非终结符，这是因为我们在进行了一次 Reduce 操作之后，会将生成式左侧的非终结符压入栈顶，并且 Reduce 操作相当于又生成了一个非终结符作为所谓的 Token，需要告诉 Parser 在吃入这个 Token 之后会转移到哪个状态。

记 $R$ 为规约动作集合：其初始化为 $\{\}$，对于每一个状态 $I$，对于每一个 $I$ 中的项 $A \rightarrow \alpha$，$R \leftarrow R \cup \{(I, A \rightarrow \alpha)\}$。因为对于可以规约的项而言，其无论下一个输入是什么，都可以规约，因此对应的 Action 行都有规约这个操作。

Shift/移进：$\mathrm{T}[i, t] = s_n$，意为在状态 $i$ 看到终结符 $t$ 时，转移到状态 $n$。
Reduce/归约：$\mathrm{T}[i, t] = r_k$，意为在状态 $i$ 看到终结符 $t$ 时，使用第 $k$ 个产生式进行规约。
Accept/接受：$\mathrm{T}[i, \$] = \mathrm{Accept}$，意为在状态 $i$ 看到终结符 EOF 时，接受整个输入，这个状态其实是 $S^{\prime} \rightarrow S \cdot \$$ 对应的项。
Goto/转移：$\mathrm{T}[i, X] = g_n$，意为在状态 $i$ 看到非终结符 $X$ 时，转移到状态 $n$。

6.4 LR(0) Parsing 过程¶

LR 分析主要围绕着状态栈的变化。实际操作：

$\operatorname*{Shift}(n)$：消耗一个输入符号，将状态 $n$ 压入状态栈栈顶；
$\operatorname*{Reduce}(k)$：弹出栈中和规则 $k$ 右侧符号数量相同的状态，在当前栈顶的状态下查找规则 $k$ 左侧的非终结符对应的 GOTO 表项 $\mathrm{goto } n$，将状态 $n$ 压入状态栈栈顶。

例子如下：

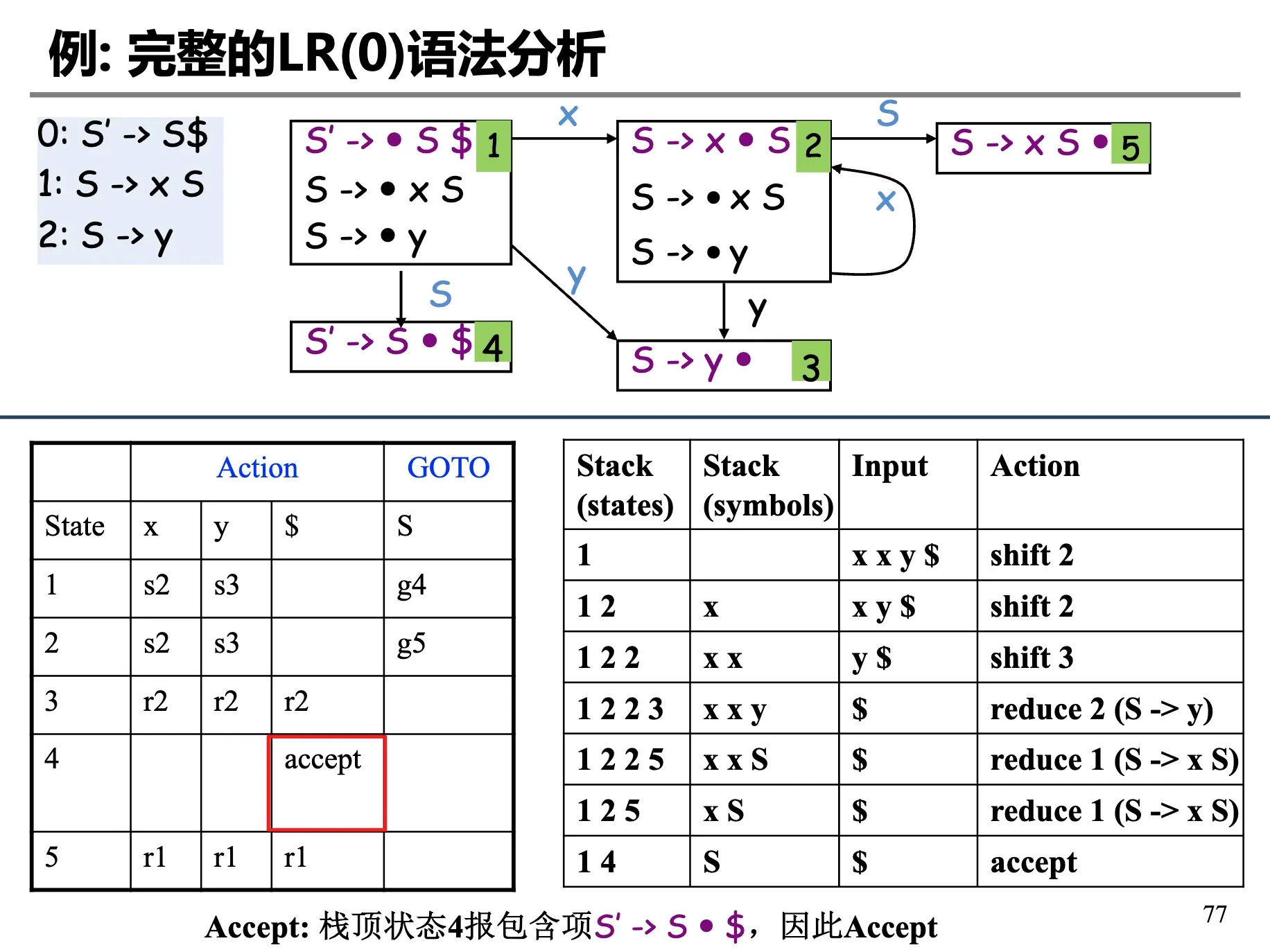
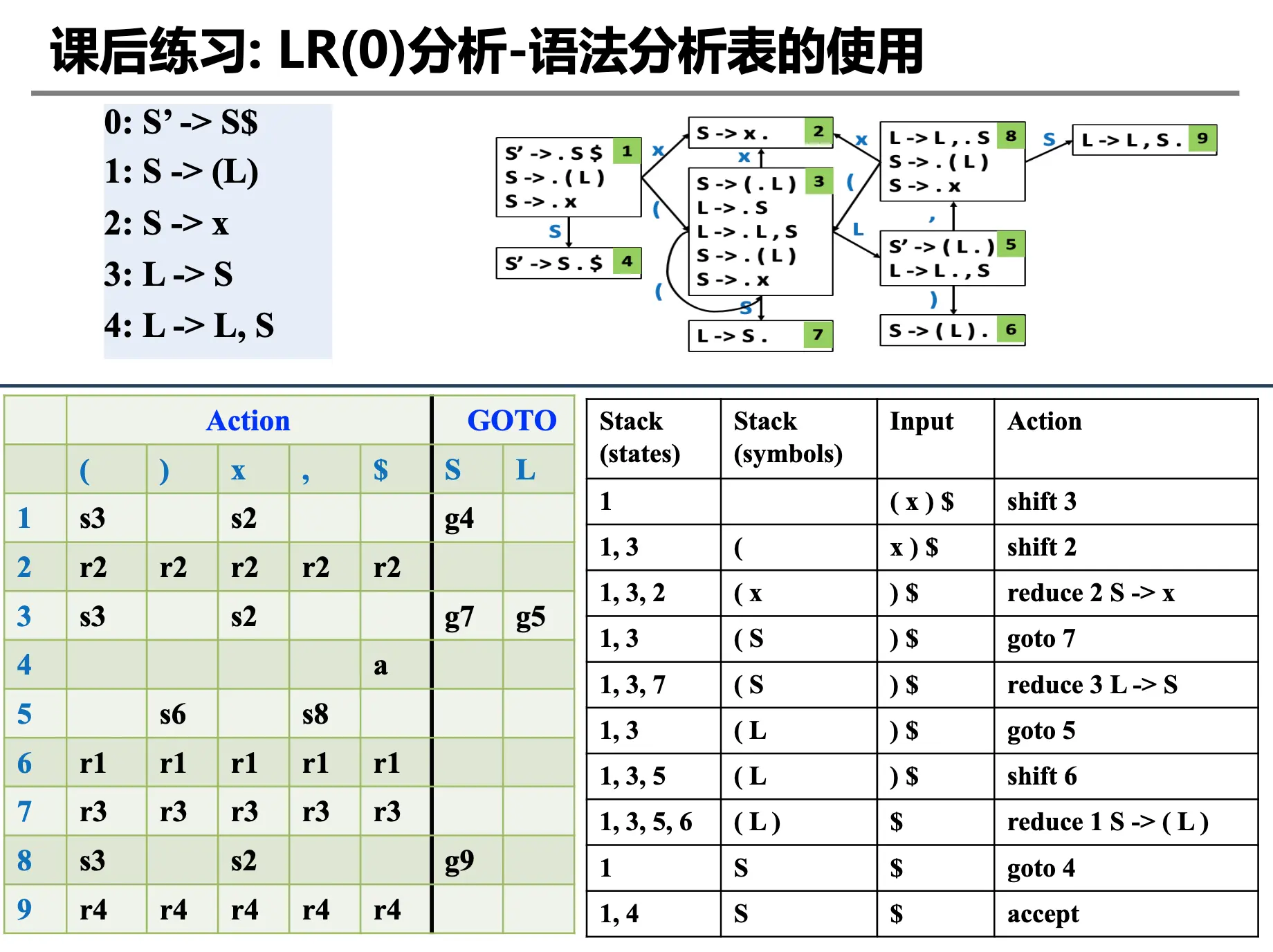
7. SLR(1) 分析¶

LR(0) 的问题在于没有 Lookahead，因为 LR(0) 的所有 Reduce 操作实际上是和状态绑定的而没有和 (状态，输入) 对绑定，因此我们在读取当前符号之前，就可以知道应该 Reduce 还是 Shift 了。并且表中也可能出现冲突：

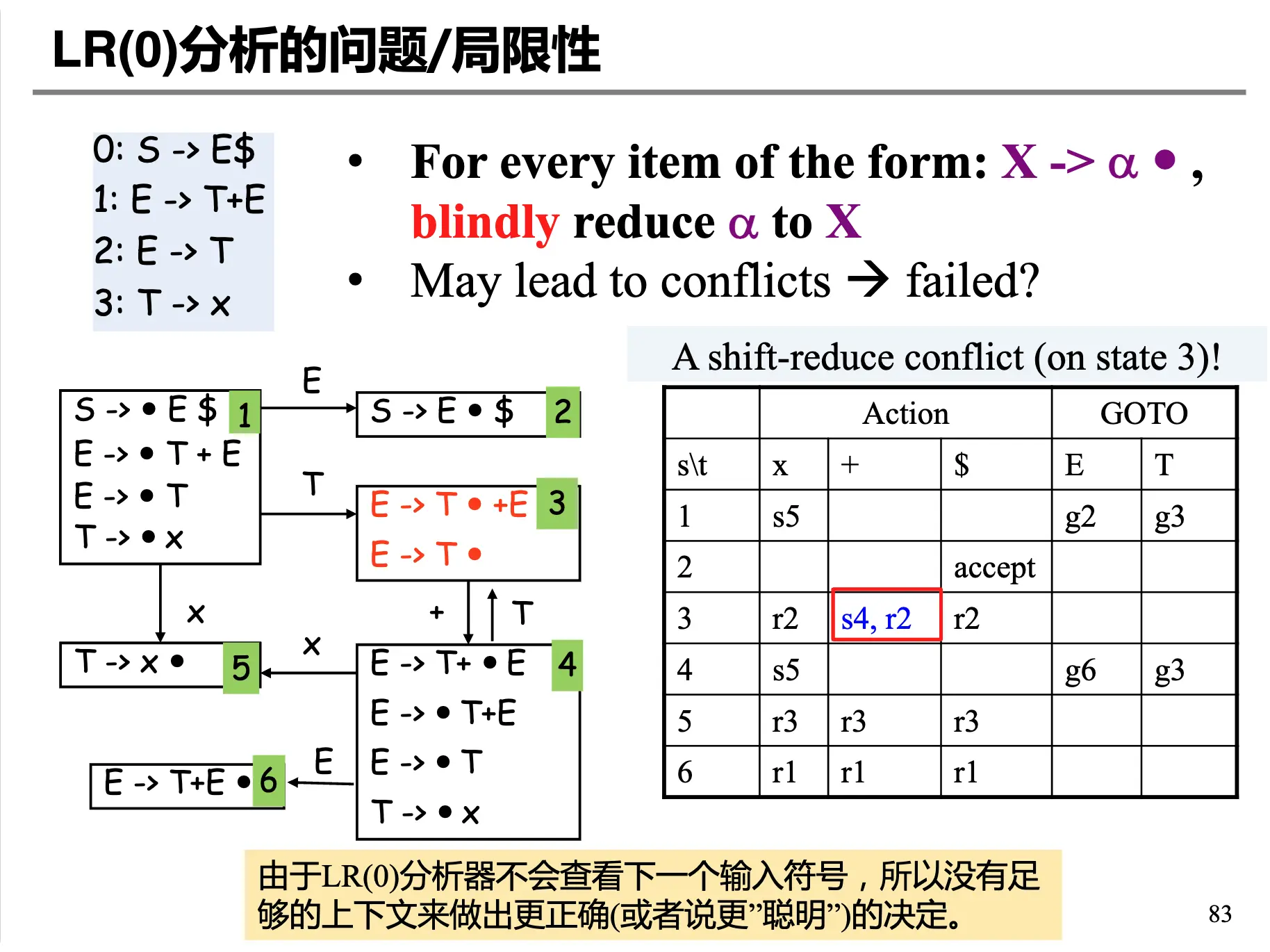
可以看出这个表中出现了出现了 Shift 和 Reduce 的冲突，由于 LR(0) 分析器不会查看下一个输入符号，因此我们需要更多的上下文来作出更加正确的决定。

SLR 分析为了解决冲突，在每次规约都加上了限制：要求每次规约时的下一个输入符号 $t \in \operatorname*{Follow}(E)$，其中 $E$ 是规约的产生式左侧的非终结符。因此对应的分析表发生了简化：

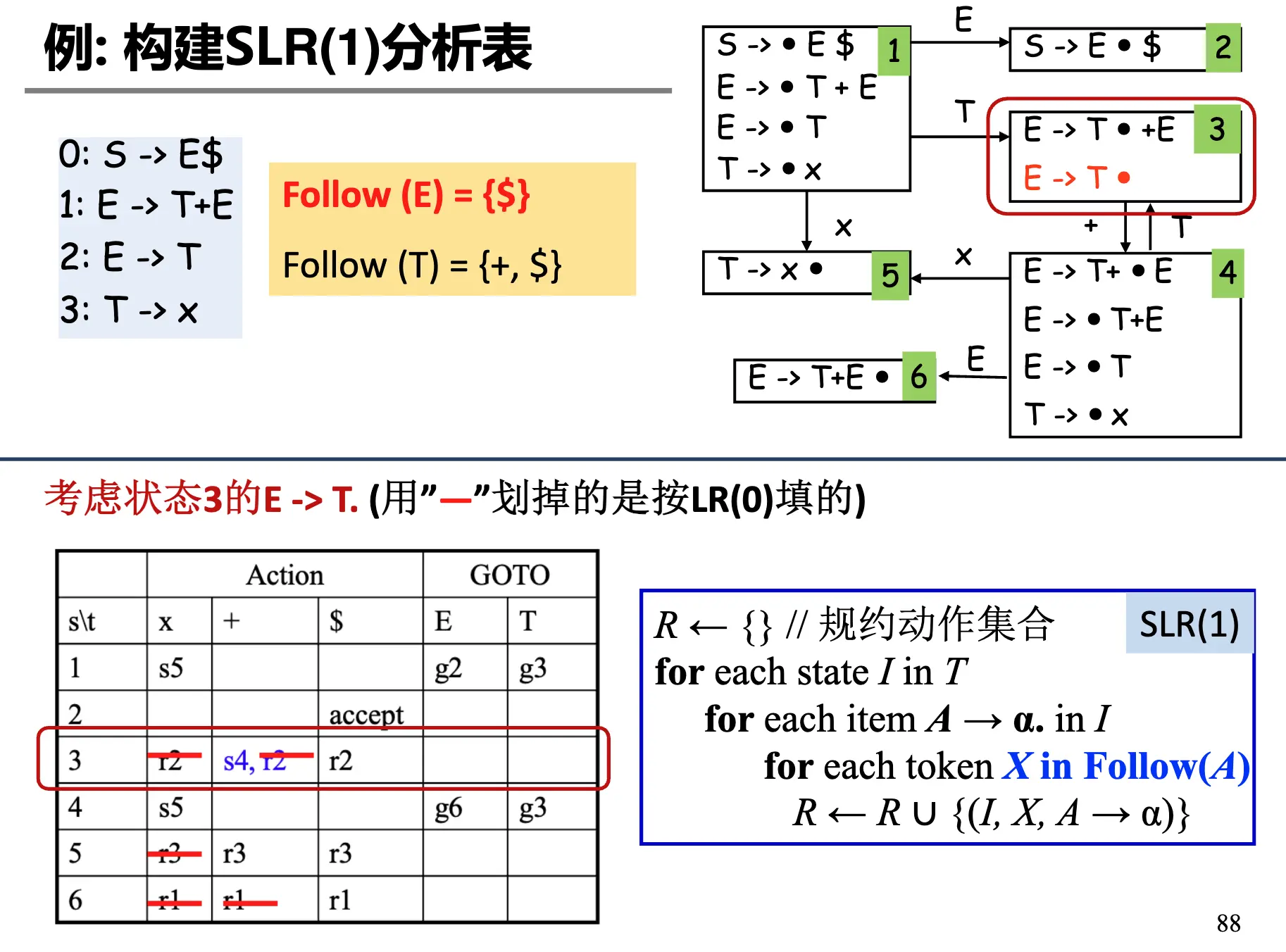
可以看出 SLR 分析和 LR(0) 的主要区别在于构造分析表时的规约动作：SLR 分析表中的条目只有当其下一个输入终结符为 $\operatorname*{Follow}(E)$ 时，才进行规约。

SLR 技术解决冲突的方法是按照 Follow 集合来限制规约：下一个输入符号必须可以按照某个句型跟在 $E$ 后面，这是因为其考虑 LR 分析过程是最右推导的逆，但是 $\operatorname*{Follow}$ 集可以看做合理但是不够精确的近似。因此我们需要更加严格的规约条件才可以进一步降低冲突的可能。

SLR 的局限性在于，我们仍然没有处理完毕所有可能的冲突：如果产生冲突的终结符正好在对应的 $\operatorname*{Follow}$ 集合中，则仍然会出现冲突，同样，两个非终结符的 $\operatorname*{Follow}$ 集合相同的时候，也可能出现多重 Reduce 冲突。

8. LR(1) 分析¶

LR(1) 的项形式为 $(A \rightarrow \alpha \cdot \beta, a)$，其中 $a$ 称为向前看符号，表示在规约之前希望看到的下一个输入终结符（可以为 $\$$），并且在输入中开头的是可以从 $\beta a$ 推导出的符号串。

$\operatorname*{Closure}(I)$：

对于状态集 $I$ 中的任意一个项 $(A \rightarrow \alpha \cdot X \beta, z)$，如果 $X$ 是一个非终结符，对于其任意一个产生式 $X \rightarrow \gamma$，对于任意的 $w \in \operatorname*{First}(\beta z)$，将 $(X \rightarrow \cdot \gamma, w)$ 加入 $I$；
重复上述过程直到 $I$ 不再变化，返回 $I$。
对于起始状态，项为 $(S^{\prime} \rightarrow \cdot S\$ ,?)$，我们并不关心 $?$ 是什么，因为 $\$$ 永远不会被移进。
在添加 $(X \rightarrow \cdot \gamma, w)$ 的时候，$w \in \operatorname*{First}(\beta z)$，事实上将 $(A \rightarrow \alpha \cdot X \beta, z)$ 的信息传递给了 $(X \rightarrow \cdot \gamma, w)$。
对于项 $(A \rightarrow \alpha \cdot, z)$，在输入开头的是可以通过 $\beta z$ 推导出的符号串，而 $w \in \operatorname*{First}(\beta z)$，新加的项 $(X \rightarrow \cdot \gamma, w)$ 表示在输入开头的是可以通过 $\gamma w$ 推导出的符号串，这样恰好不冲突。

$\operatorname*{Goto}(I, X)$：

初始化 $J$ 为空集；
对于状态集 $I$ 中的任意一个项 $(A \rightarrow \alpha \cdot X \beta, z)$，将 $(A \rightarrow \alpha X \cdot \beta, z)$ 加入 $J$；
返回 $\operatorname*{Closure}(J)$。

Reduce Action:

初始化 $R$ 为空集；
对于状态集 $T$ 的任何一个状态 $I$，对于 $I$ 中的任意一个项 $(A \rightarrow \alpha \cdot, z)$，将 $(I, z, A \rightarrow \alpha)$ 加入 $R$；
动作 $(I, z, A \rightarrow \alpha)$ 表示在状态 $I$ 上，当向前看符号为 $z$ 时，解析器将使用规则 $A \rightarrow \alpha$ 进行规约。这限制了每一个规约操作的下一个符号。

LR(1) 分析的局限非常直接：Parsing Table 太大了，可能包含过多种状态。并且文法仍然可能因为 R-R 冲突与 S-R 冲突从而导致其不属于 LR(1)！这样的例子可以在 LR(k) 且 $k > 1$ 的文法中大量找到。

9. LALR(1) 分析¶

构造方法：

一种是构造完整的 LR(1) 分析表，然后合并具有相同核心的状态；
另一种是构造 LR(0) 分析表，然后计算向前看符号;
我们只讲解第一种方法。

对 LR(1) 分析而言，很多状态除了向前看符号都是相同的，因此我们可以按照某种规则合并这些状态。

核心/Core：一组 LR(1) 项的核心是这些项的第一个部分（不包括向前看符号）。具有相同核心的 LR(1) 状态可以被合并，比如 $\{[X \rightarrow \alpha \cdot, a], [Y \rightarrow \beta \cdot, c]\}$ 和 $\{[X \rightarrow \alpha \cdot, b], [Y \rightarrow \beta \cdot, d]\}$ 可以合并为 $\{[X \rightarrow \alpha \cdot, a, b], [Y \rightarrow \beta \cdot, c, d]\}$。这被称为 LALR(1) 状态。

合并方法如下：

选择两个具有相同核心的 LR(1) 状态；
每次合并删除这两个状态，并且创建一个新的状态，这个状态包含这两个状态的并集；
按照原先的入边出边方法链接新状态，同时需要修改 GOTO 表以反映合并。
直到所有的状态的核心都不同。

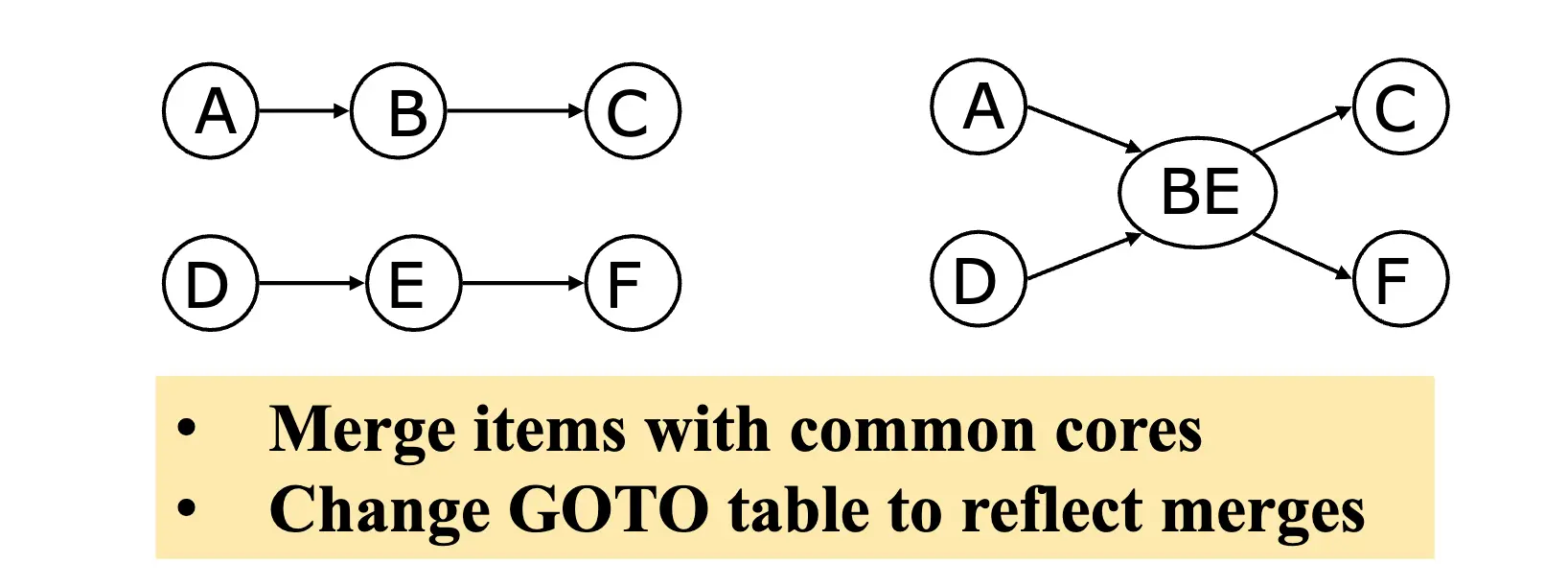
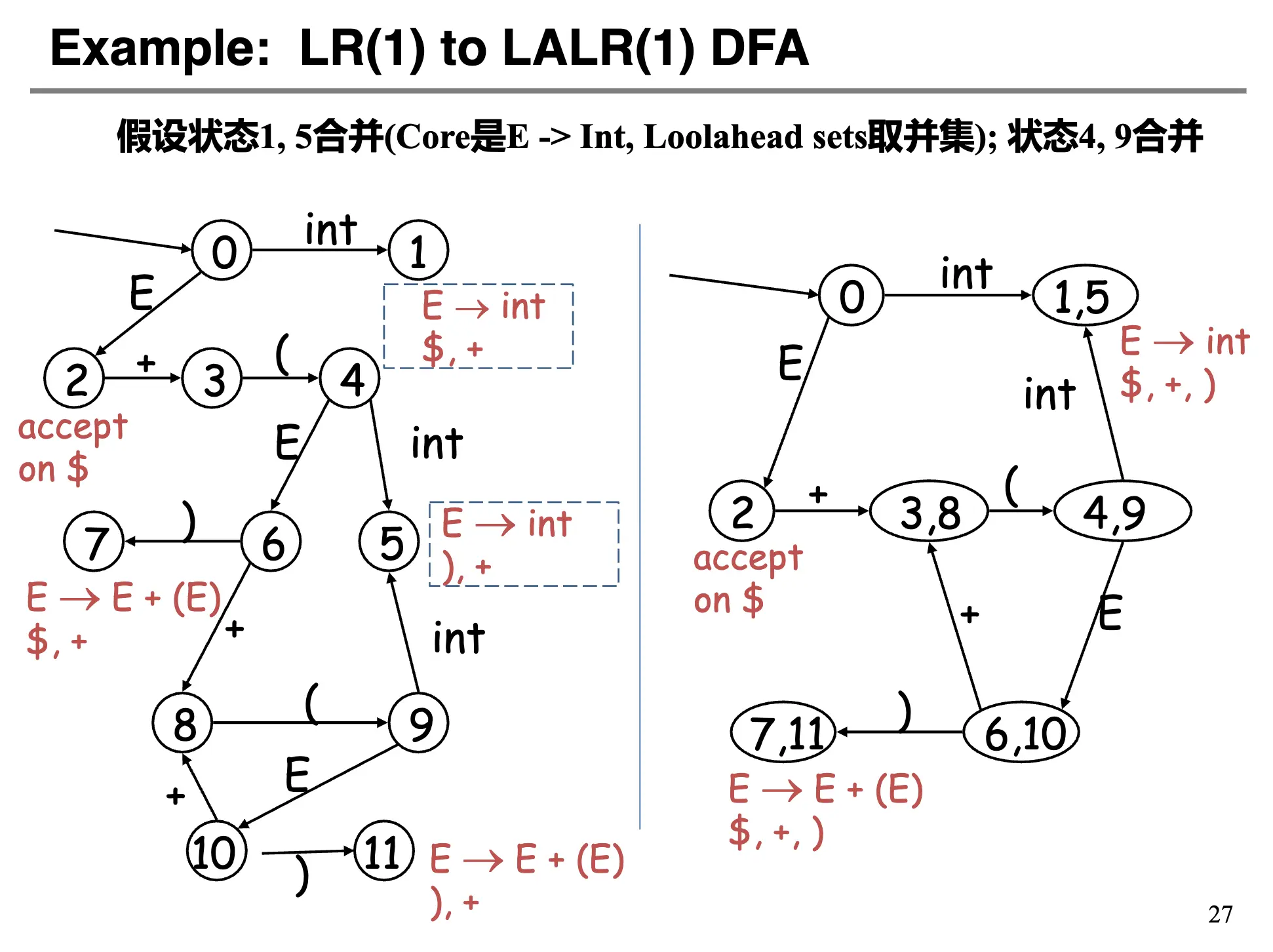
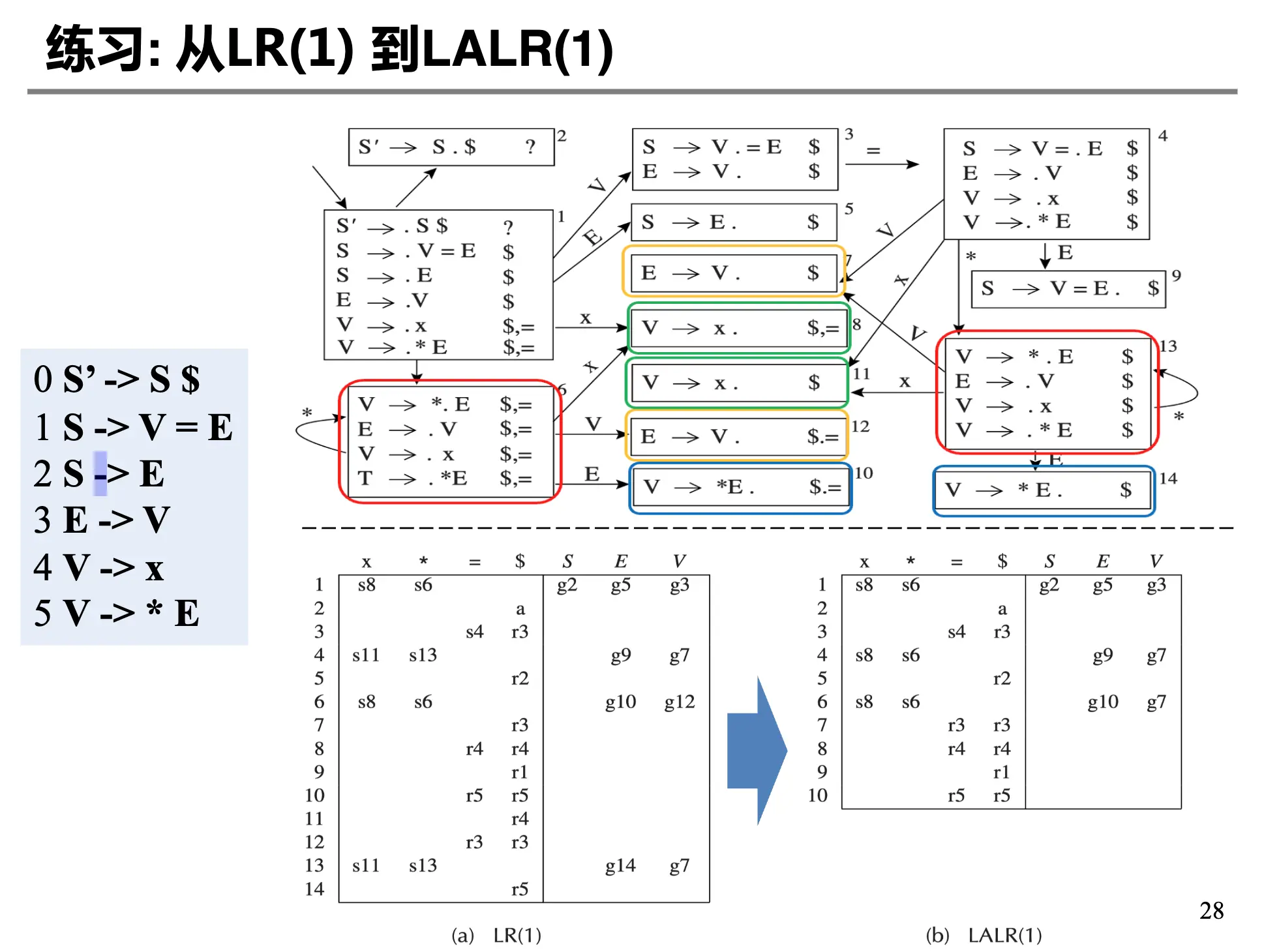
注意到：LALR(1) 还是会出现冲突：比如合并的状态为 $\{[X \rightarrow \alpha \cdot, a], [Y \rightarrow \beta \cdot, b]\}$ 和 $\{[X \rightarrow \alpha \cdot, b], [Y \rightarrow \beta \cdot, a]\}$，则合并之后的状态为 $\{[X \rightarrow \alpha \cdot, a, b], [Y \rightarrow \beta \cdot, a, b]\}$，则会出现冲突。

但是出现这种冲突的可能性还是很小的，因为 LALR 的表达能力足够强大。并且 LALR 分析表和 SLR 的一样大，已经可以高效处理大部分的程序设计语言。

10. Parser Generator¶

Yacc：基于 LALR，使用 BNF/Backus-Naur Form 形式书写，其 GNU 版本为 Bison。

Yacc 源程序为 trans.y，经过 Yacc 编译器输出为 trans.tab.c，然后经过 C 编译器输出为 trans.o。