Topic 8:指令选择¶
约 1984 个字 12 张图片 预计阅读时间 7 分钟
Outline
1. 概述¶
编译器后端主要完成下面三件事:
- 指令选择/Instruction Selection:将 IR 转换为抽象汇编代码;
- 寄存器分配/Register Allocation:决定哪些值可以放在寄存器中;
- 指令调度/Instruction Scheduling:通过重排等操作优化代码、实现指令级并行。(但是本课程不覆盖)
抽象汇编/Abstract Assembly 指的是具有无限个寄存器的汇编代码,其为中间值创建新的寄存器,在之后会将这些寄存器分配给物理寄存器。
我们需要解决的问题在于:IR 的一个语句有多种可能的实现方式,需要确定为其中“最好”的一种。一般有下面几种翻译方式:宏展开/Macro Expansion、树覆盖/Tree Covering 和 DAG 覆盖/DAG Covering。我们主要使用树覆盖,树状的 IR 天然适合寻找树上的模式匹配。
我们使用 Jouette 指令集,其是一种 RISC-V 风格的,Load/Store 架构的指令集,数据/地址能直接在寄存器中放得下,寄存器 r0 是零寄存器,每一个指令都需要一个时钟周期,除了 MOVEM 寄存器需要 m 个时钟周期。
树类型/Tree Pattern 指的是可以匹配一个 IR Tree 的一部分的模板,每一个树类型都对应着一个机器指令。一个树类型也叫做一个 Tile。指令选择的目标是使用一个不互相覆盖的树类型集合覆盖掉 IR Tree,这样就可以将 IR Tree 转换为汇编代码序列了。可以把 Tiling 想象成铺地板的过程,每一个 Tree Pattern 就是各种大小不一的地砖,指令选择就类似于使用地砖铺满屋子。理论来讲,只要我们的 Tree Pattern 足够小且丰富,比如可以覆盖掉单一节点,我们就很有机会将程序对应的 IR Tree 完全覆盖掉。
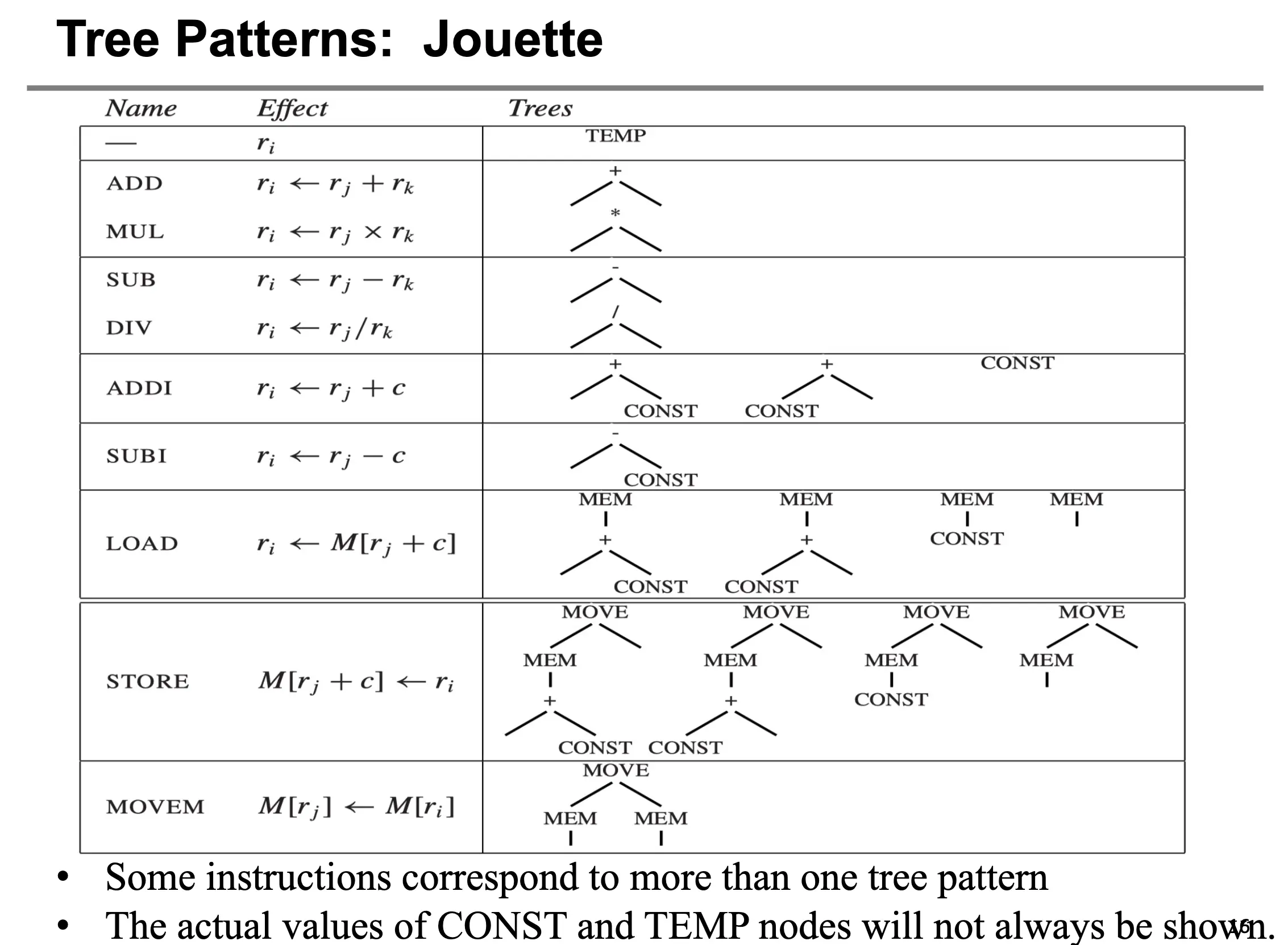
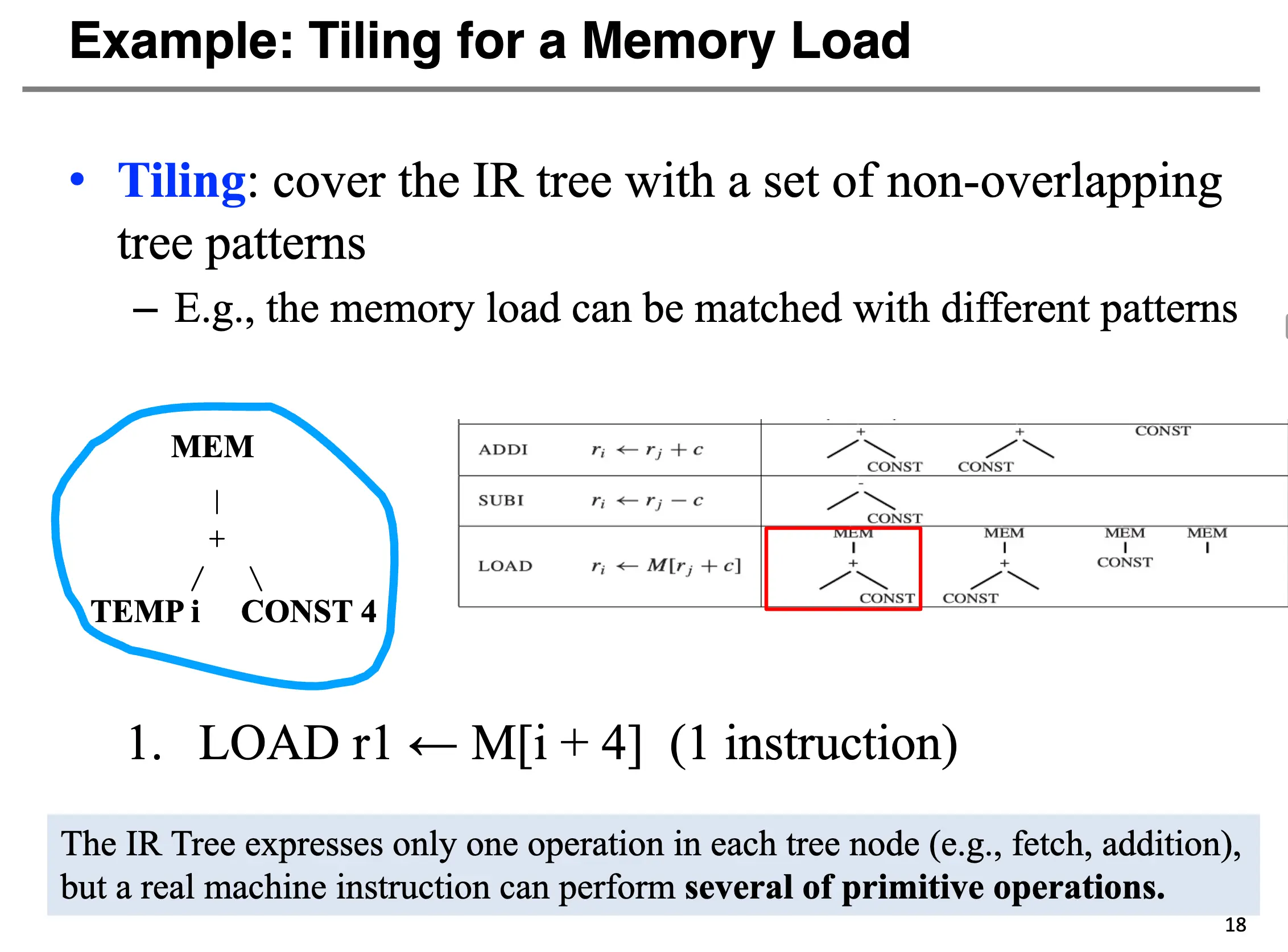
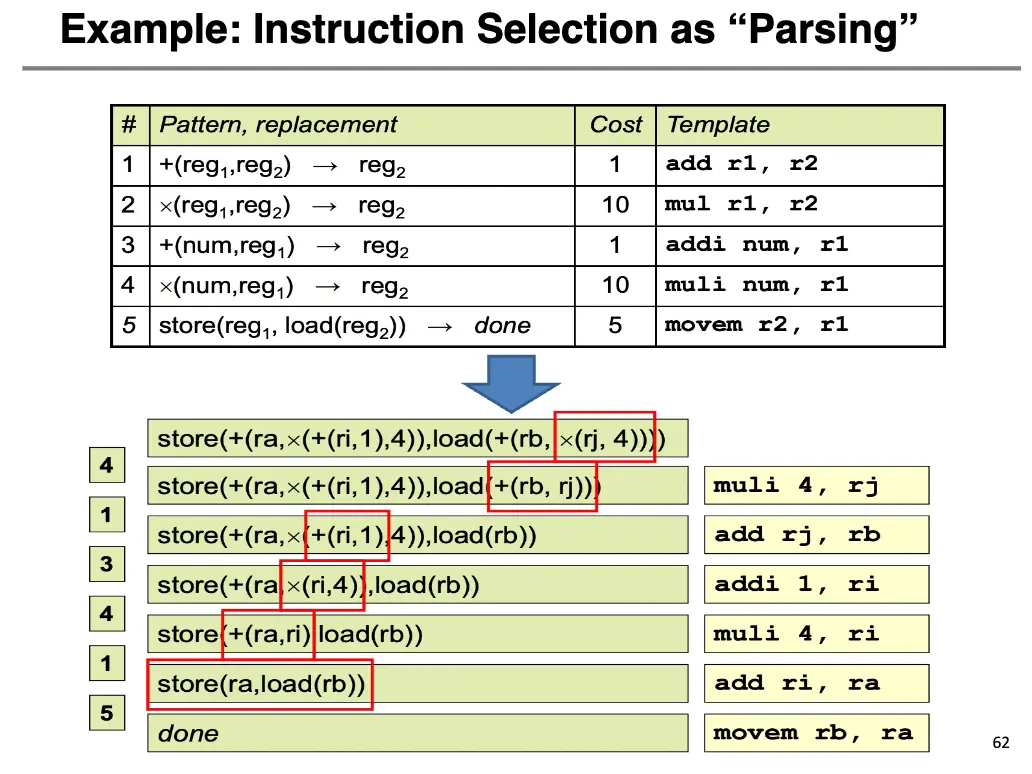
下面就是指令选择的一个例子:

注意到第 1、3、7 部分并不对应着任何机器指令,其只不过是虚拟寄存器/临时值。
指令选择需要量度来评价选择的结果有多少,理想情况下需要考虑指令代价、运算对象和结果如何存储等等因素。比如从硬盘到主存再到寄存器,速度越来越快,但是容量越来越小,这就需要一定的权衡。我们可以选择比较小的 tiles,确保我们可以覆盖掉每一个 IR Tree,但是这样可能需要更多的 tiles/instructions,然而大量的指令并不一定意味着时钟周期数目庞大,比如 RISC-V 的绝大部分指令都只需要一个时钟周期,CISC 的某些指令需要十个或者更多的时钟周期。
- 全局最优/Optimum Tiling:所有的 tiles 的代价之和最小;
- 局部最优/Optimal Tiling:没有两个相邻的 tiles 可以合并成一个 tile 了。
全局最优 Tiling 一定是局部最优的,但是反过来不一定。
2. 指令选择算法¶
简单说来,指令选择算法分为两种:Maximal Munch 和 Dynamic Programming。其中 Maximum Munch 是寻找一个局部最优的 Tiling,采用贪心、自顶向下的策略;Dynamic Programming 是寻找一个全局最优的 Tiling,将每一个节点都分配一个 cost 并使用从底而上的方法。
2.1 Maximal Munch¶
Maximum Munch 采用一个基本假设:更大的 tiles 就是更优的。所谓最大的 tile 就是节点数目最多的 tile,对于两个节点数目相同的 tile,我们随便选择一个当更大的。
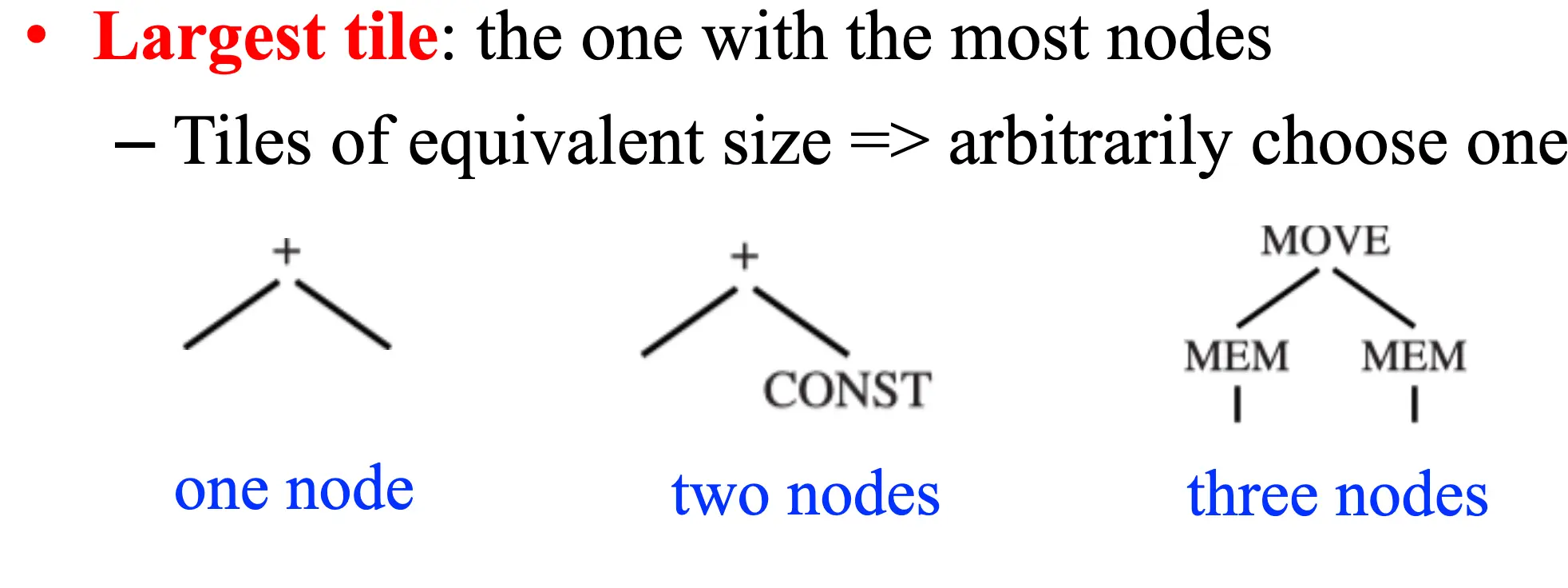
主要思想是从顶部开始,使用最大的 tile 覆盖当前节点,然后递归的对剩下的子树应用该算法,对于两个一样大的 tile,随便选一个或者选择 cost 更小的那个。最后使用 Postorder 的顺序遍历树,子节点的顺序依赖于具体节点的要求。按照顺序发射指令序列,并且使用相同的寄存器链接 tile 边界(当两个 tile 之间需要传递数据的时候)。
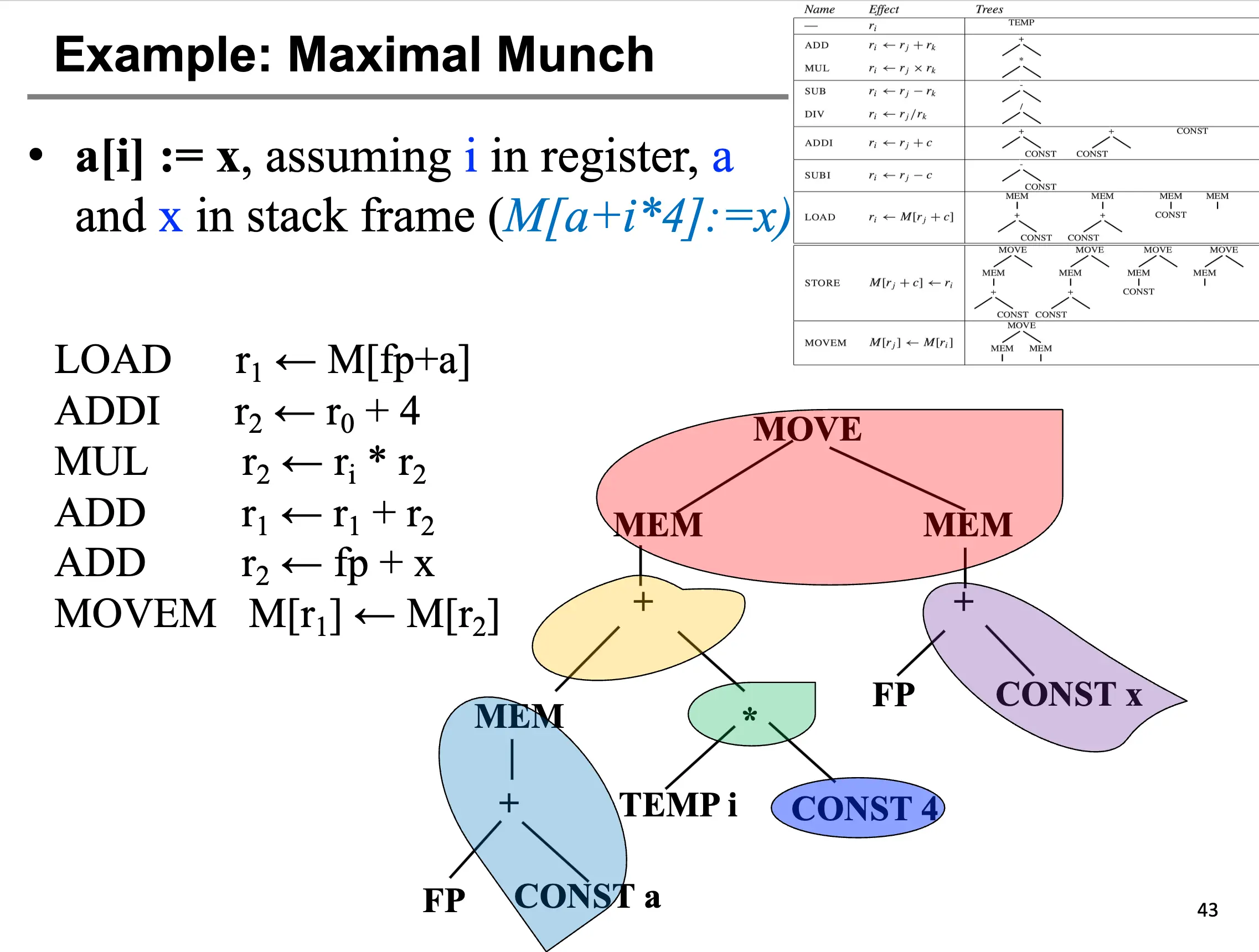
2.2 Dynamic Programming¶
动态规划算法的目标是寻找一个全局最优的 Tiling,将每一个节点 \(t\) 都分配一个代价 \(c_t\),然后匹配 \(t\) 的代价为 \(c_t + \sum_{y \in \operatorname*{leaves}(t)} c_y\)。方法如下:
- 从底向上计算出每一个子树的最优 tiling 代价;
- 对于每一个节点,考虑所有的匹配 tiles;
- 对每一个匹配的 tile,计算其代价为当前 tile 的代价加上所有子节点的代价;
- 选择最小代价的 tile 作为当前节点的最优 tiling。
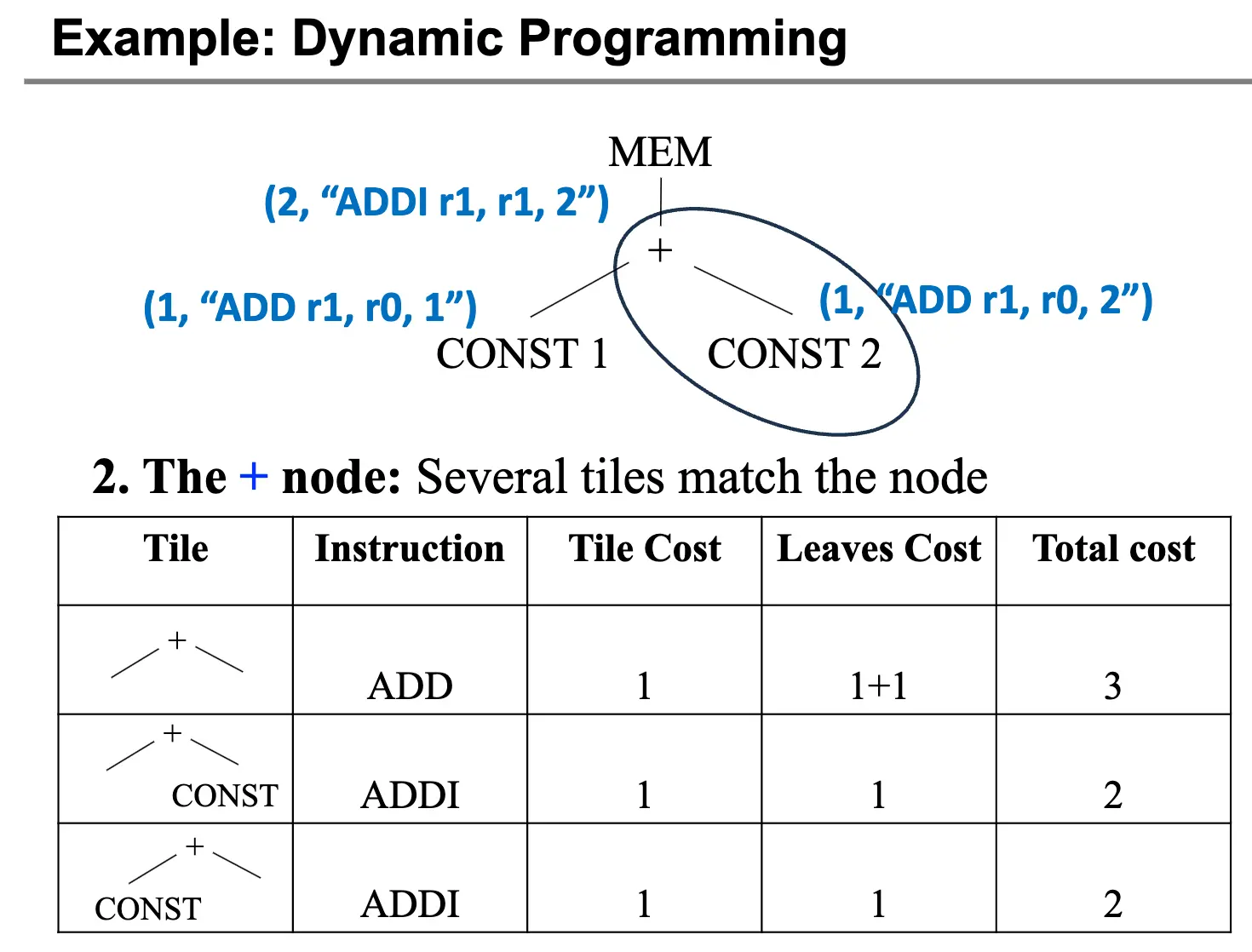
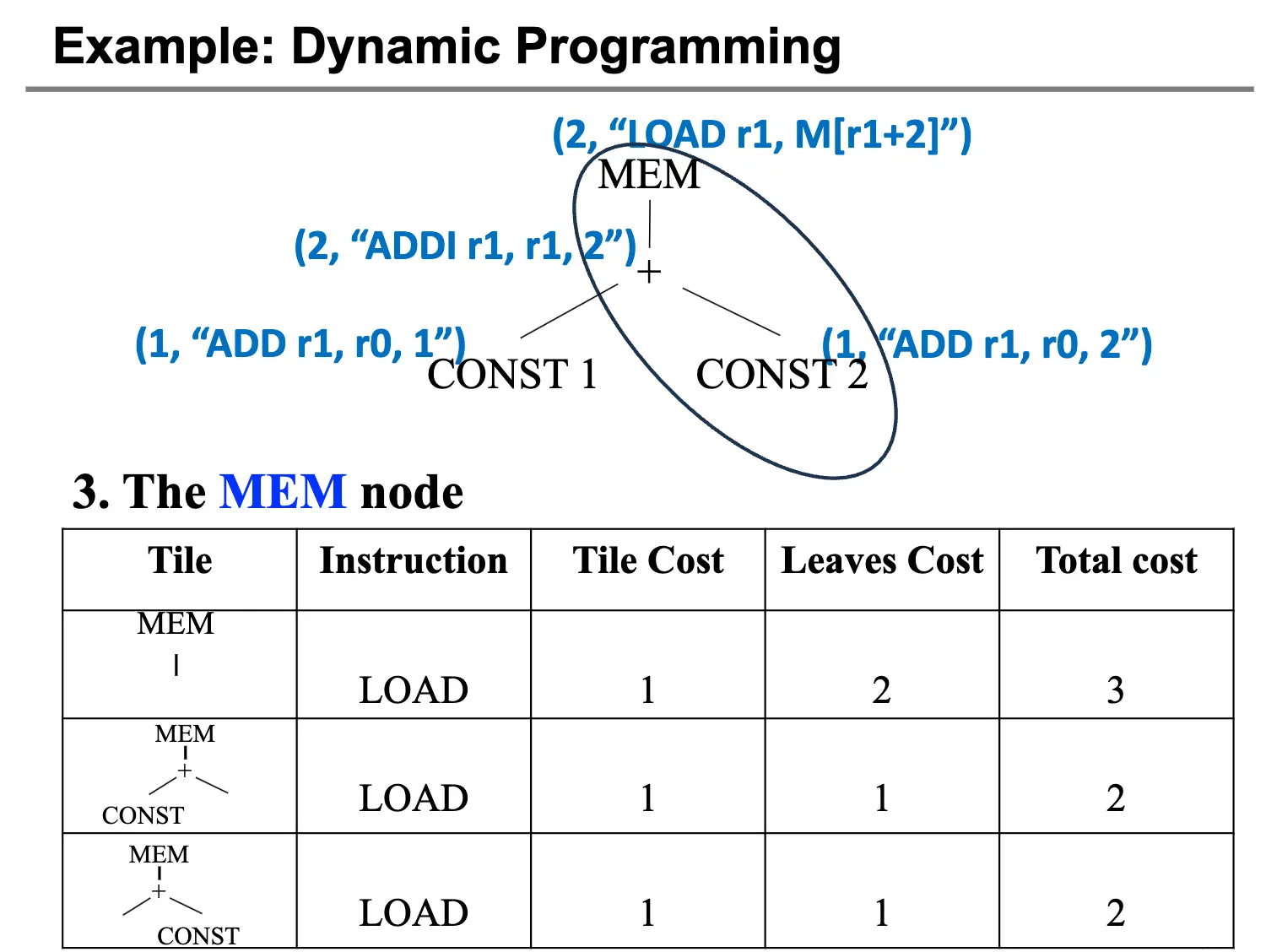
比如对于 MEM(BINOP(PLUS, CONST(1), CONST(2))),计算 CONST(1) 和 CONST(2) 的代价与 tile 都是显然的,使用 ADDI 指令,代价为 1。接下来 + 节点的最优 tile 显然是使用 ADDI 指令,然后 MEM 节点显然是使用带常数的 LOAD 指令:
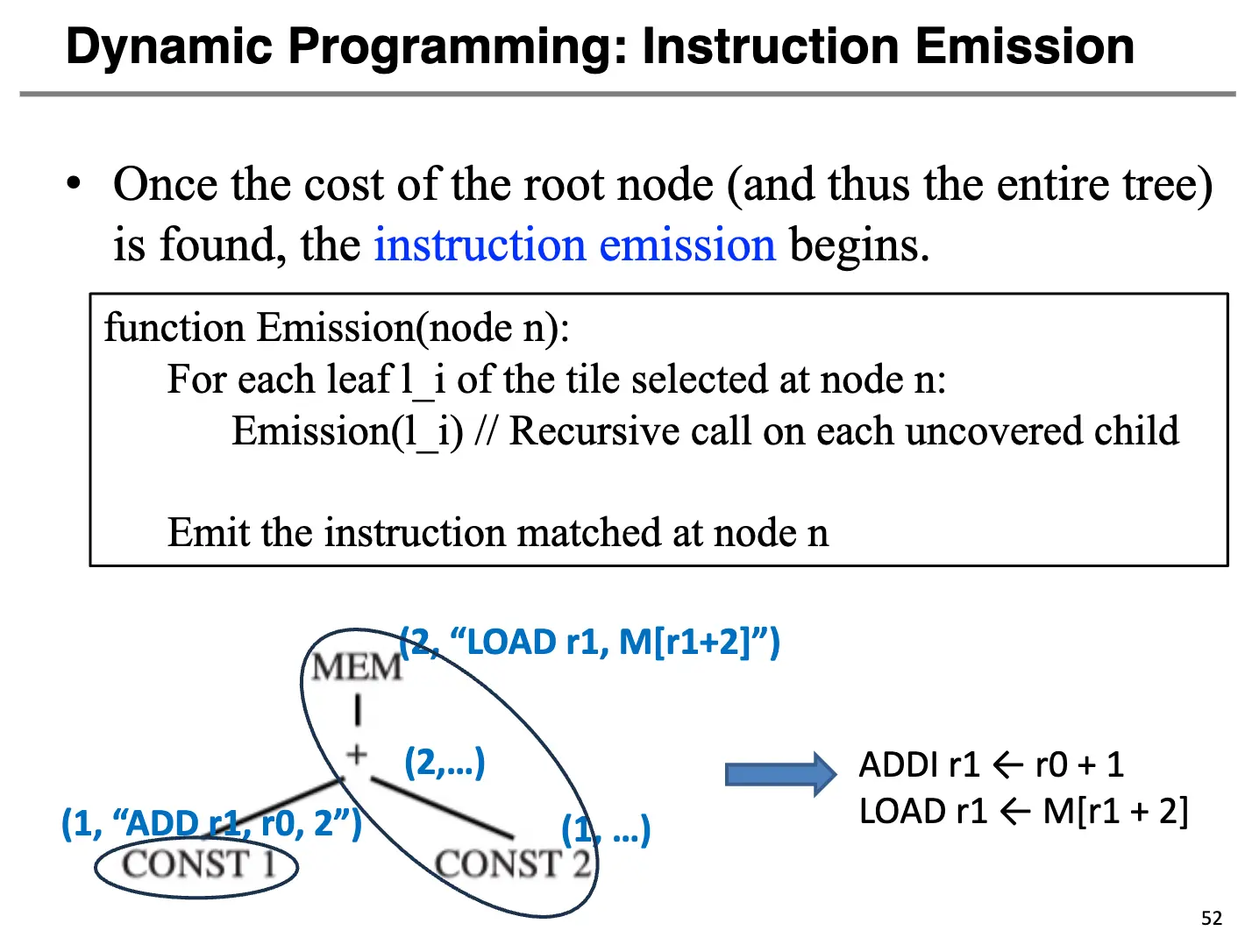
一旦根节点的代价被确定之后,整棵树的代价也就确定了,因而指令序列也就确定了,我们开始发射指令。我们将其处理成递归函数,所以实际上是从底开始发射的。因为根节点只有一个子节点 CONST 1,所以发射 CONST 1,然后发射完了再发射根节点的指令。
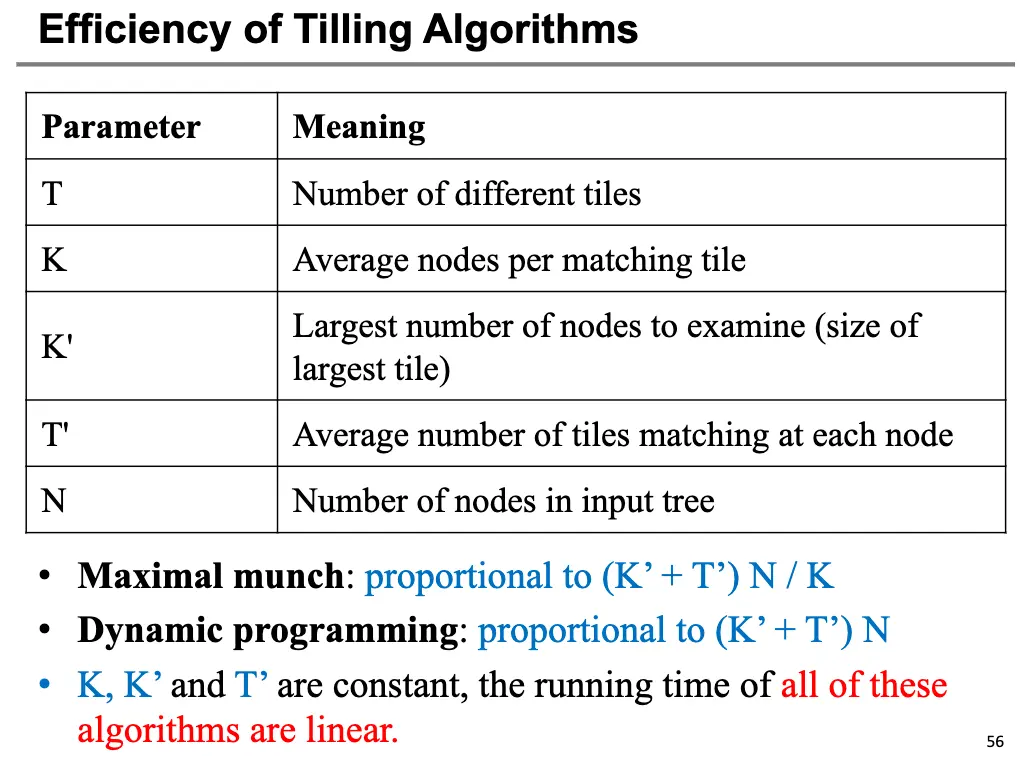
两个算法的效率如下,这意味着两个算法其实都是线性复杂度的:
3.3 树文法/Tree Grammar¶
动机在于,对于复杂指令集架构并且有多种寄存器类别和寻址模式的机器来说,很难使用简单的树模式和覆盖算法。我们的目标在于需要指令选择器生成器/Instruction Selector Generator,使用一个单独的规约之中定义 tile,并且使用一个更加通用的树模式匹配算法来计算覆盖。
解决方法是使用树文法进行指令选择,将指令选择问题规约成一个 parsing problem,使用动态规划算法的一个泛化形式进行分析。树文法是上下文无关文法的一种,需要记录的如下:
- Pattern:一个树类型。比如
+(reg1, reg2); - Replacement:这个 Pattern 被替换之后,在原来位置上使用什么代替,比如
+(reg1, reg2) -> reg2; - Cost:tile 的固有代价;
- Template:生成的目标代码模板。
树文法可能是有歧义的/Ambiguous。
指令选择的工具现在还很多,比如 Twig、BURG 和 LLVM TableGen。
3. CISC 和 RISC¶
差别简单列表如下:
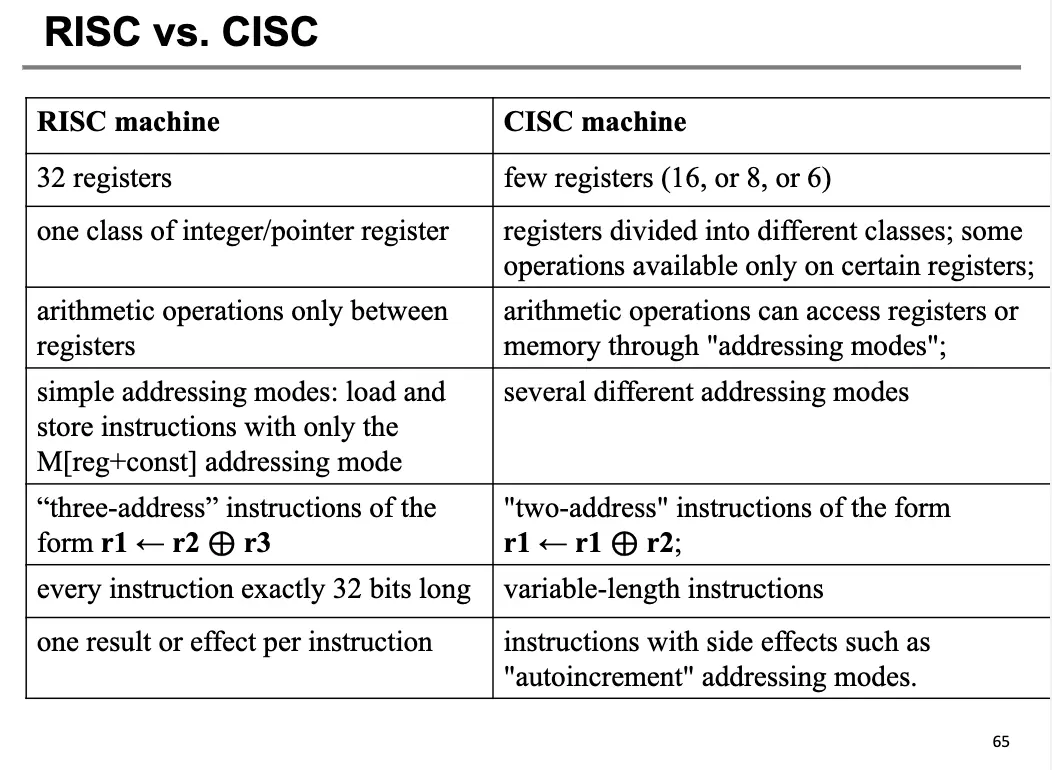
对于 RISC 来讲,全局最优和局部最优的覆盖一般没啥区别,因为 RISC 指令一般代价相近,都很小,但是对于 CISC 来讲,全局最优和局部最优差别就很大了,因为有的复杂指令可能组合了多个操作。因此,对于 RISC 来讲,简单的覆盖算法就已经足够了。
CISC 还引入了一些问题:
- 寄存器数量较少:解决方法是自由生成一些临时节点,让寄存器分配器进行优化,决定什么时候溢出;
- 要求操作数和结果放在不同寄存器:多显式 move 即可,比如 Pentium 要求左操作数放在
eax,结果的高位放在rdx,解决方法是将操作数和结果显式的传送到对应的寄存器; - 使用双地址指令:添加额外的移动指令,让寄存器分配器进行优化;
- 使用内存操作数:为内存操作数添加新的 tile;
- 复杂寻址模式:为常见的地址计算创建新的 tile。
还有一个问题就不赘述了:
