跳转至

Topic 10：寄存器分配

约 2981 个字 16 张图片 预计阅读时间 10 分钟

Outline

1. 概述

为什么要进行寄存器分配？原因在于程序使用无限多个临时的变量，抽象汇编也使用无限多个寄存器，但实际上真实的机器只有有限多个寄存器，就需要我们在保持程序语义不变的基础上，将临时值映射到寄存器上。同时也做一些性能的优化。

在 LLVM 中，典型的就有四种寄存器分配算法，分别为 Basic、Fast、Greedy、PBQP。我们主要学习图染色寄存器分配。

2. 图染色寄存器分配

2.1 干扰图

核心想法：如果两个临时值不在同一时间活跃/活跃区间不重合，那么他们就可以使用一个寄存器，否则就称这两个变量之间干扰。这样我们就可以构建一个干涉图/Interference Graph：

  • 节点表示临时值或者虚拟寄存器；
  • 边将两个在同一时间活跃的节点连接起来，表示它们不能使用同一个寄存器，注意在构建干扰图的时候，一个变量的活跃区间从其定义之后的下一个指令才开始算。
  • 颜色表示物理寄存器，一条边上两个节点不能有相同的颜色。

目标是将干涉图染色，其中颜色的数目和物理寄存器数目相同，并且每个节点只能有一种颜色。

Interference Graph

需要特别处理的情况在于涉及 MOVE 指令的情况，对于一条定义了一个变量 \(a\) 的指令，其出口活跃变量集合为 \(b_1, \cdots, b_j\)，可以按照下面方法添加干扰边：

  • 如果这是一条非 MOVE 指令，则对 \(a\) 和 \(b_1, \cdots, b_j\) 都添加干扰边；
  • 如果这是一条 MOVE 指令 MOVE a, c，则对 \(a\) 和 \(b_1, \cdots, b_j\) 中不等于 \(c\) 的变量都添加干扰边，常见做法是对于等于 \(c\) 的变量添加一个虚线连接的边，后续在合并阶段会有用。
  • 但是，如果后续有一条对 \(a\) 的非 MOVE 定义，且这时候 c 还是活跃的，那么还需要添加干扰边 (a, c)。

Interference Graph

2.2 图染色概述

目标有两个：

  • 顶点染色/Vertex Coloring：为图中每个顶点分配一种颜色，使得任何相连的两个顶点颜色不同。
  • K-染色/K-Coloring：在顶点染色的基础上，规定最多只能使用 \(k\) 种颜色。

方法如下：

  • 首先根据活跃区间构建出来一个干扰图；
  • 对这个干扰图进行顶点染色，使得任何相连的两个顶点颜色不同；
  • 如果需要的颜色超过 \(K\) 个，就进行溢出/Spilling。

那么最终的图染色的问题有多难呢？

  • 找到一个最小的 \(K\) 使得图是可以被 \(K\) 染色的：这是一个 NP-hard 问题；
  • 给定一个常数 \(K\)，判断图是否可以被 \(K\) 染色：这是一个 NP-complete 问题；

因此我们需要一些启发性方法，或者近似算法。一般情况下不需要找到最小的 \(K\)，或者甚至可以误判一个可以被 \(K\) 染色的图为不可 \(K\) 染色的。

3. 通过简化进行着色

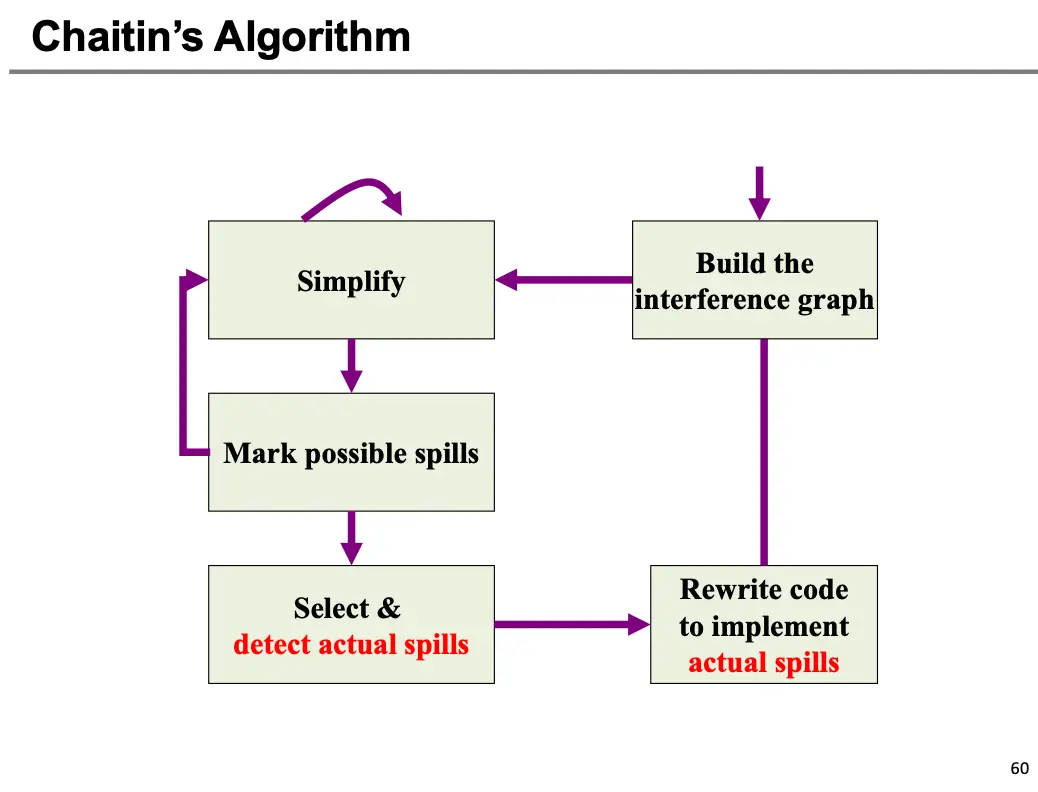
我们的算法大纲分为四个阶段：建图/Build、简化/Simplify、溢出/Spill、选择/Select。

3.1 简化与选择

定理：如果一个图 \(G\) 包含一个度小于 \(K\) 的节点，那么删掉这个节点和其关联的边可以得到一个子图 \(G^{\prime}\)，如果这个子图可以被 \(K\) 染色，那么原图也可以被 \(K\) 染色。

这个定理实际上引出了基于栈的、简单的染色算法，想法如下：

  • 建图/Build：还是按照之前的规则构建干涉图；
  • 简化/Simplify：不断从图中删除度小于 \(K\) 的节点，压入栈中，直到所有节点都被删除（很乐观）；
  • 溢出/Spill：啥都不干（很乐观）；
  • 选择/Select：从栈中弹出节点，重建图，并为其分配一个颜色，这样的染色操作一定可以完成。

但是这样的启发性算法很可能失败，而且就在简化阶段的删除节点那一步就失败了，因为可能在某一个时刻，不存在度小于 \(K\) 的节点，但是这不意味着这个图不可以被 \(K\) 染色，山人自有妙计。

3.2 溢出/Spilling

上面启发性算法失败的解决方法之一是：我们可以选择图中的某些节点，选择将其溢出到内存之中，这样就可以避免在简化阶段失败。

我们引入一种方法，叫做乐观着色/Optimistic Coloring，核心想法是：如果在某一个时刻图中的所有节点的度都大于等于 \(K\)，我们可以标记一个节点为潜在溢出/Spill Candidate，假设其不和别的节点干涉，将其直接删除、压入栈中，然后继续简化，如果最终可以成功染色，那就万事大吉。在下面这个图上，我们先删除 \(d\)，然后假设 \(b\) 可以直接被乐观删除，结果如下：

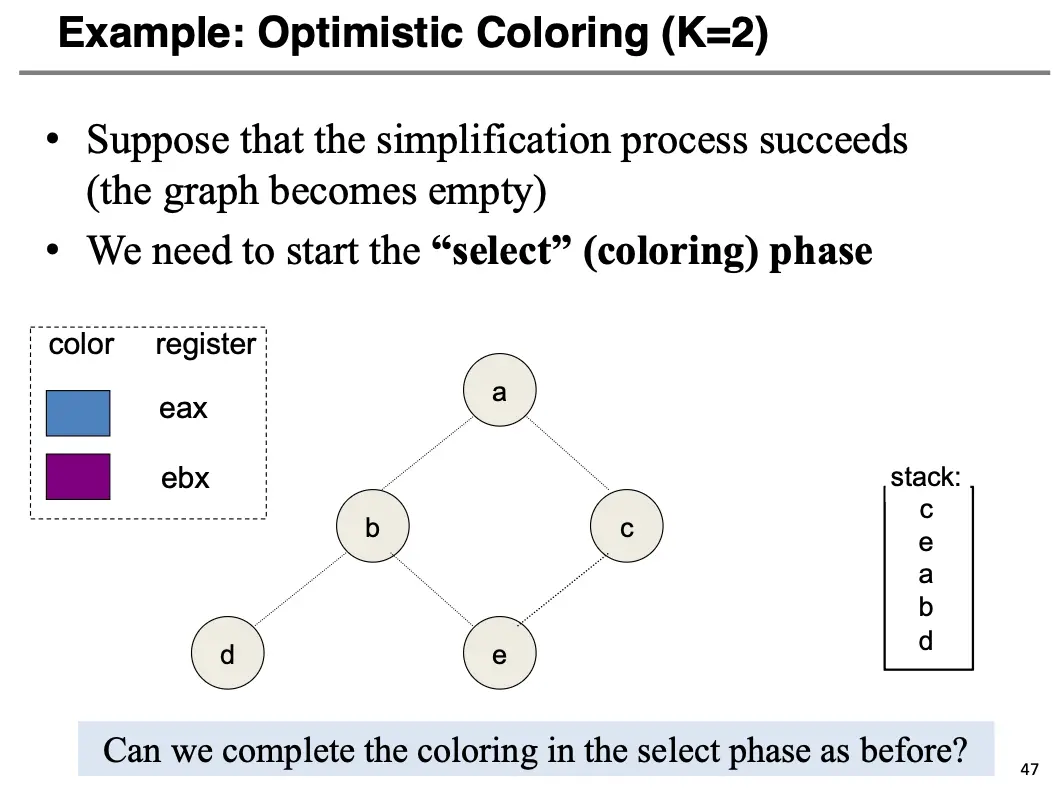
Interference Graph

然后我们尝试进行图重建和染色，问题在于，我们乐观估计可以删除 \(b\)，但是事实上对 \(b\) 是否可以成功染色是没有把握的，如果 \(b\) 的邻居都被染了色，并且颜色数目小于 \(K\)，那么我们就可以成功染色，也不需要实际上溢出。上张图实际上是可以按照我们的算法完成染色的，但是对于下面这个图就做不成了：

Interference Graph

这时候就需要我们执行溢出了：如果这个节点的邻居已经染了 \(K\) 种颜色，那么执行一次真正的溢出，不给这个节点染色，然后继续选择阶段，鉴别溢出或者正常染色。

Interference Graph

然后需要我们修改代码，对溢出的节点分配栈帧内存，当每一次使用溢出节点时，都先从栈帧中加载，对于每一次定义溢出节点之后，都将其存储到栈帧上。

下面是一个可以不用溢出就染色的例子，练一下：

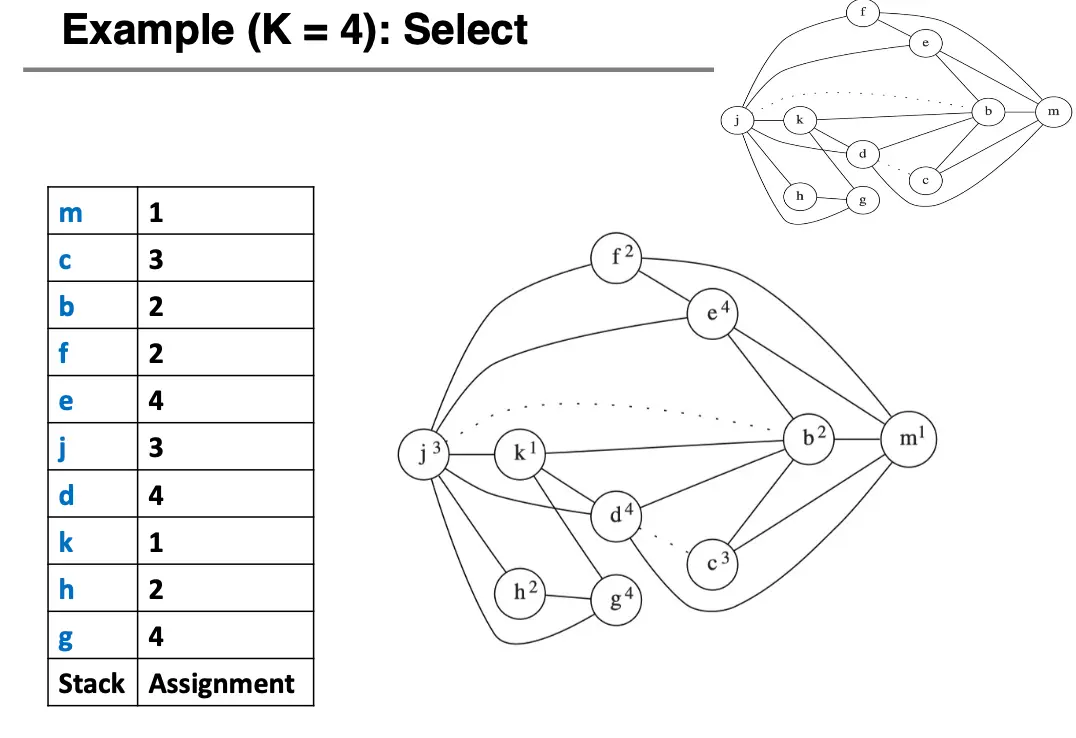
Interference Graph

3.3 合并/Coalescing 与冻结/Freezing

合并/Coalescing：给定一个 MOVE 指令 MOVE a, b，如果 \(a\) 和 \(b\) 之间没有干涉边，那么就可以将这个 MOVE 指令删除，并且将 \(a\) 和 \(b\) 合并成一个节点。

合并的优点在于可能提升可染色性，减少溢出概率；但是也有可能添加干涉边的数目，让这个图不可染色。因此合并的策略为保守合并，并不执行会让染色更难的合并。一般有下面两个准则：

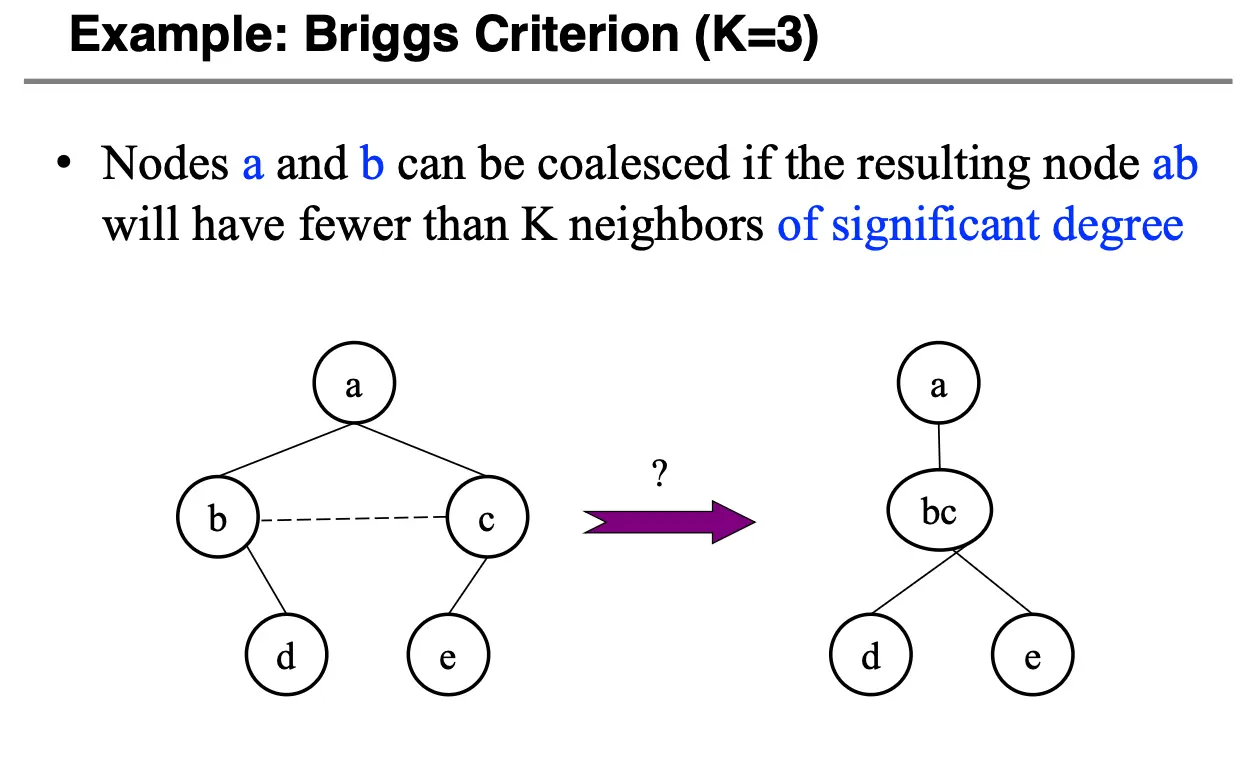
  • Briggs 条件：如果两个互不干涉的节点合并后，新节点的 significant 邻居数目小于 \(K\)，那么就可以合并，这里的 significant 邻居数目是指度数大于等于 \(K\) 的邻居数目；
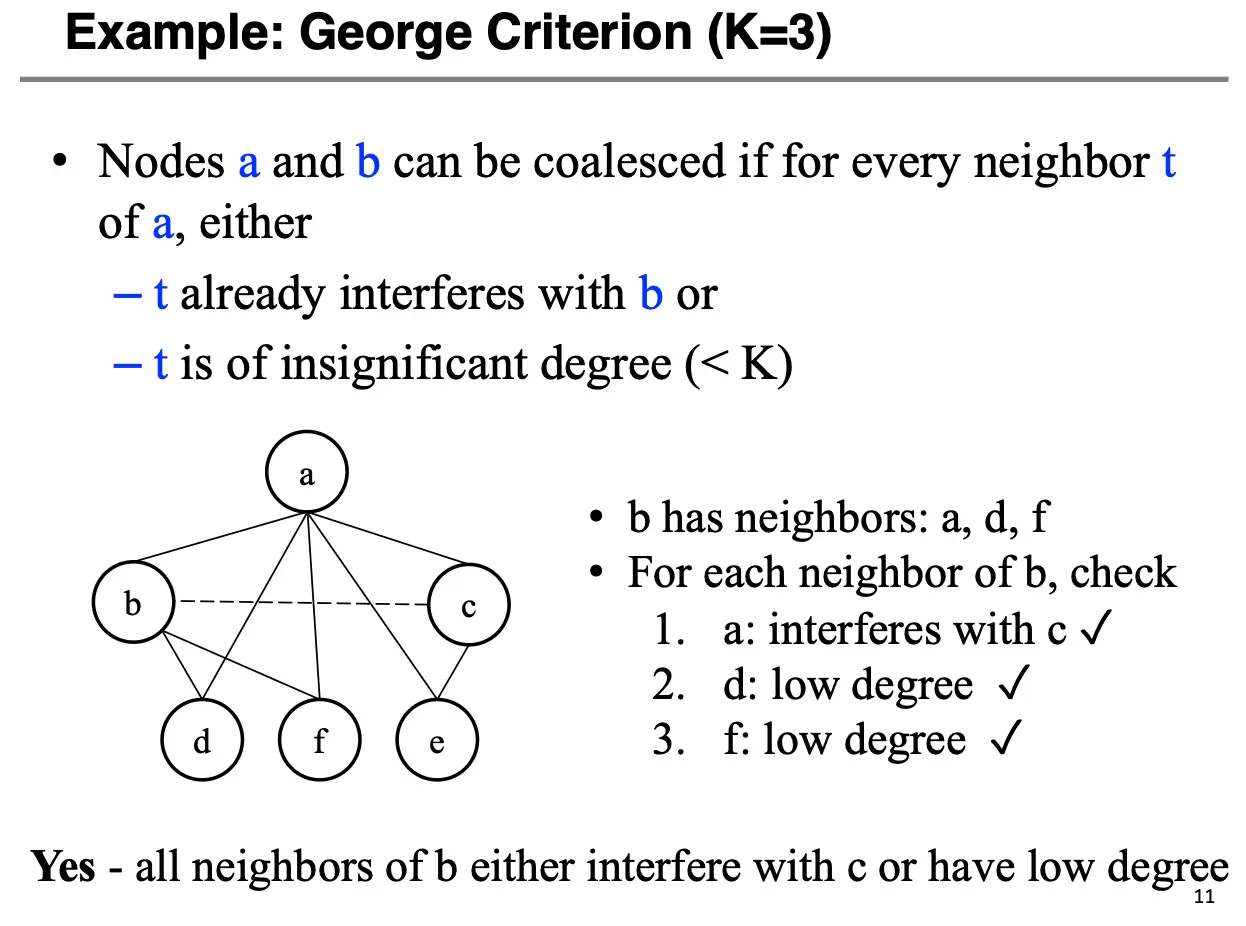
  • George 条件：如果要合并互不干涉的节点 \(a\) 和 \(b\)，对于 \(a\) 的每个邻居 \(t\)，要么 \(t\) 和 \(b\) 干涉，要么 \(t\) 的度小于 \(K\)，那么就可以合并。

这两个准则都是安全的，可以保证不将一个可以被 \(K\) 染色的图变为不可被 \(K\) 染色的图。下面分别对两个准则举例子：

Briggs Condition

George Condition

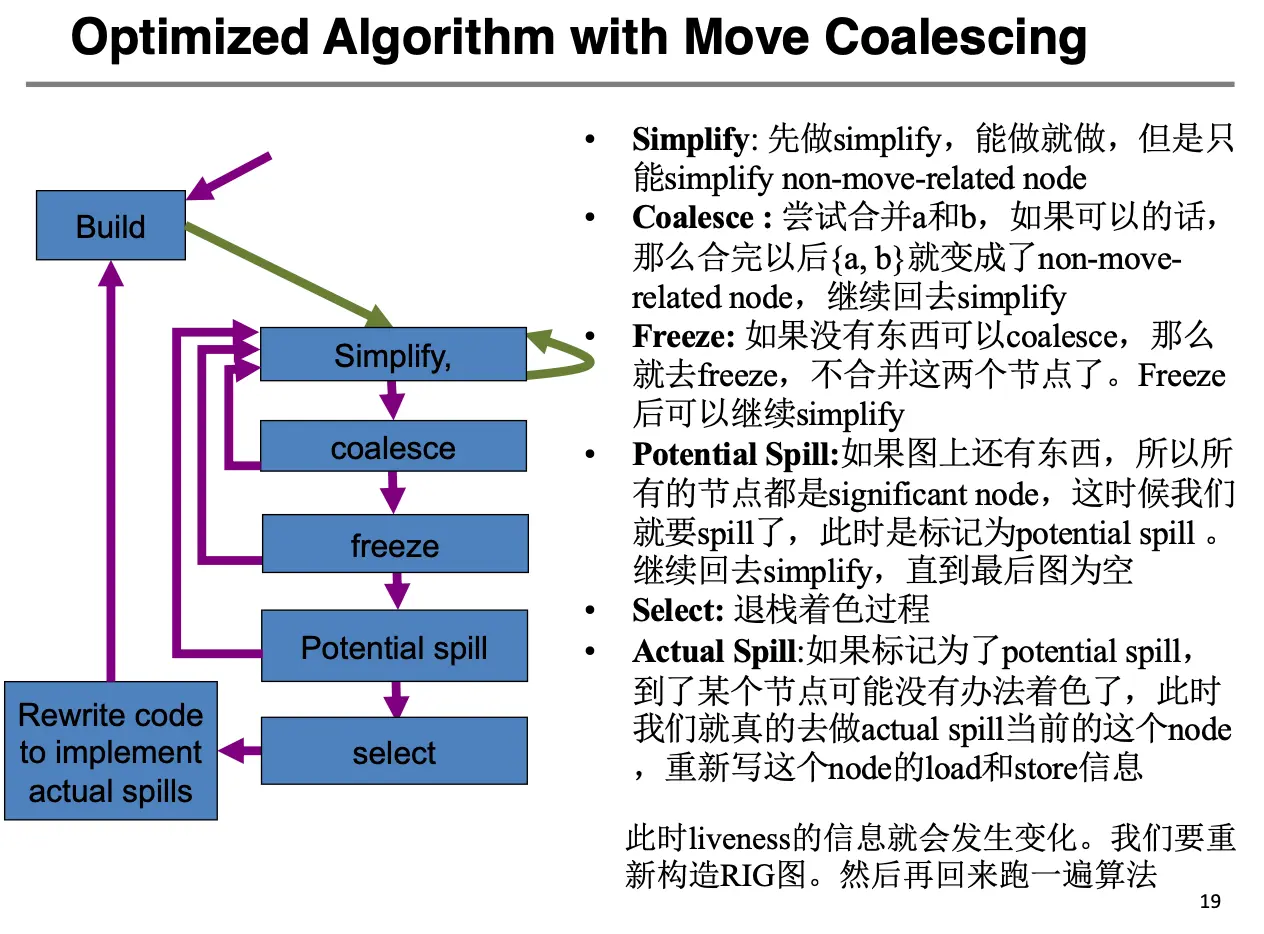
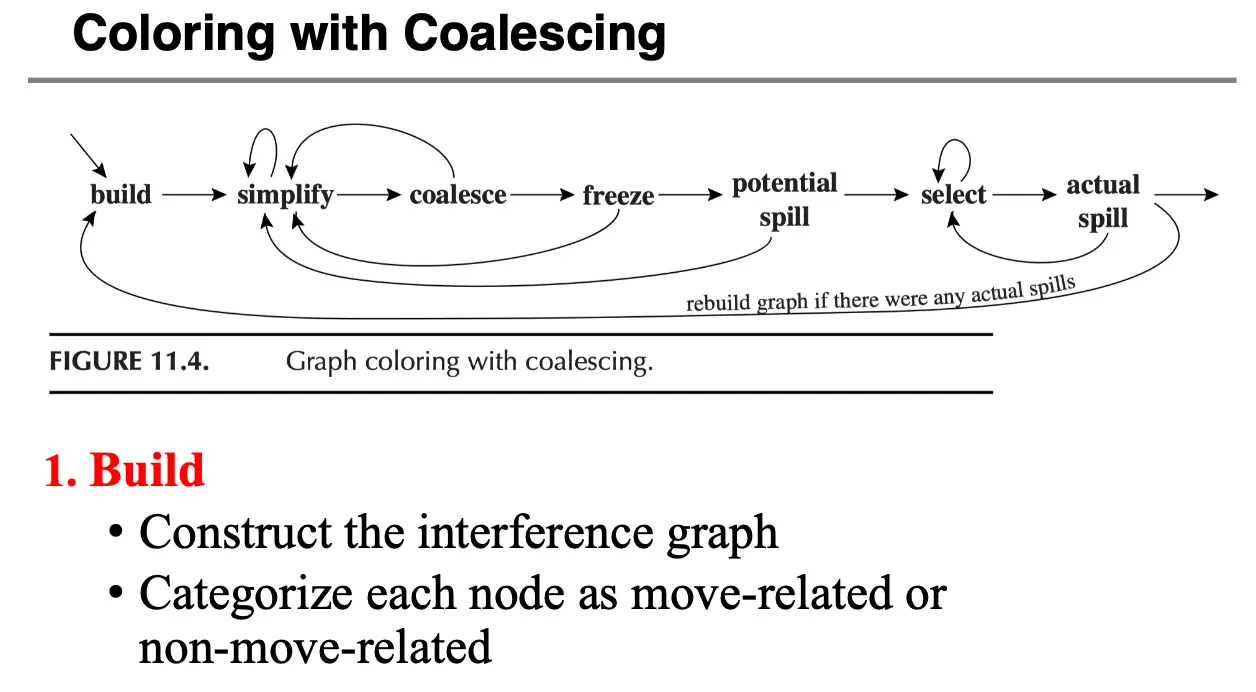
在考虑了 MOVE 指令与合并之后，我们可以将算法流程总结为如下，这里新加了一个冻结操作，讲得很清楚了：

  • 建图/Build：构建干涉图，并为 MOVE 指令添加虚线边；
  • 简化/Simplify：不断从图中删除度小于 \(K\) 的、不和 MOVE 指令有关（没有虚线边）的节点，压入栈中；
  • 合并/Coalesce：针对和 MOVE 指令有关的节点执行保守合并；简化和合并操作一直进行直到只剩下度数比较大的节点和与 MOVE 指令有关的节点；
  • 冻结/Freeze：如果既无法简化也无法合并，那么选择一个和 MOVE 指令有关的、低度数的节点，将其连接的虚线边去掉，然后重新进行简化和合并；
  • 溢出/Spill：如果必要的话，也就是只剩下度数大的节点了，选择节点标记为潜在溢出，然后继续进行简化和合并；
  • 选择/Select：从栈中弹出节点，重建图，并为其分配一个颜色；
  • 实际溢出/Actual Spill：如果选择阶段失败了，重写代码并且实现真正的溢出，重新构建图，然后重新开始整个算法。

Algorithm

Algorithm

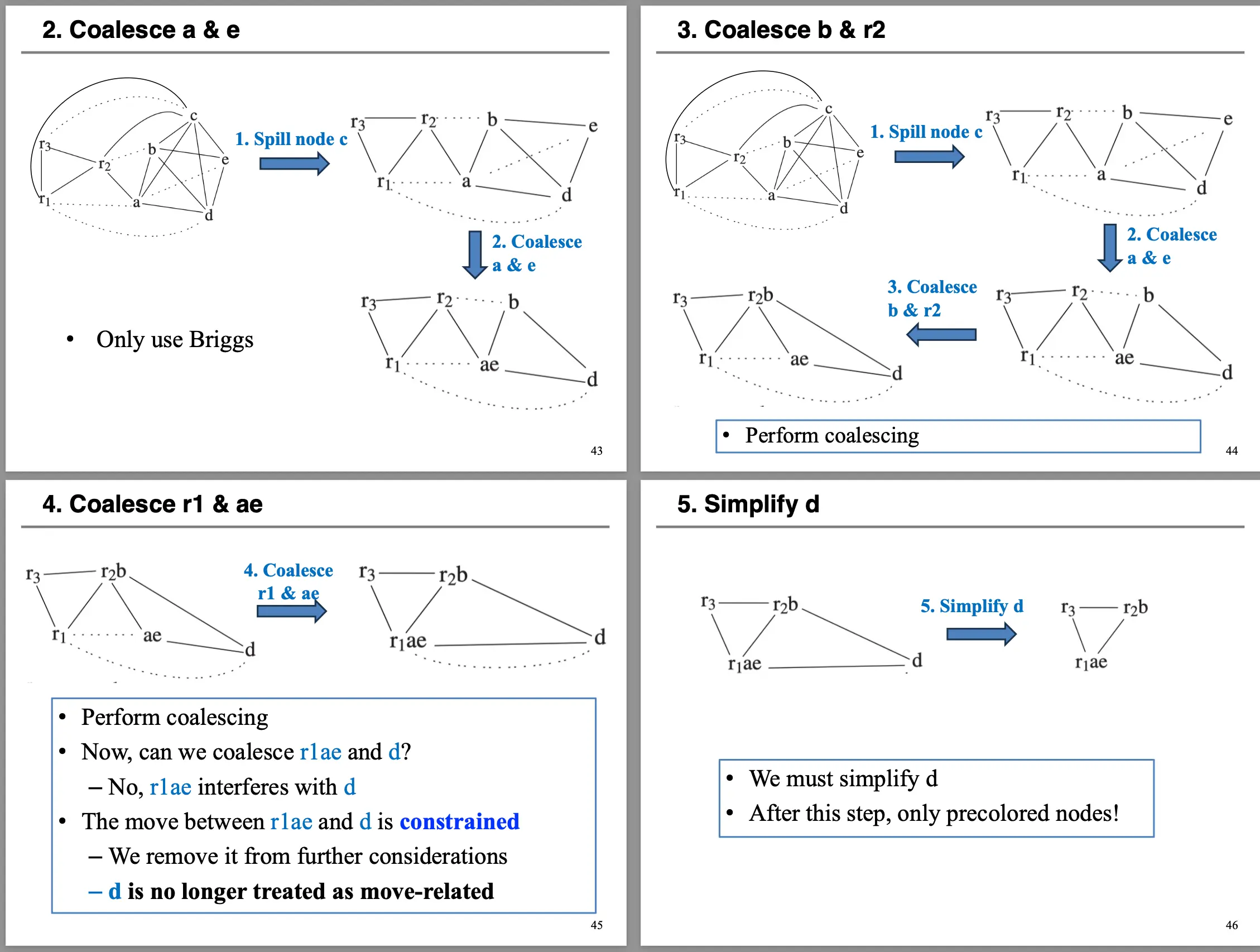
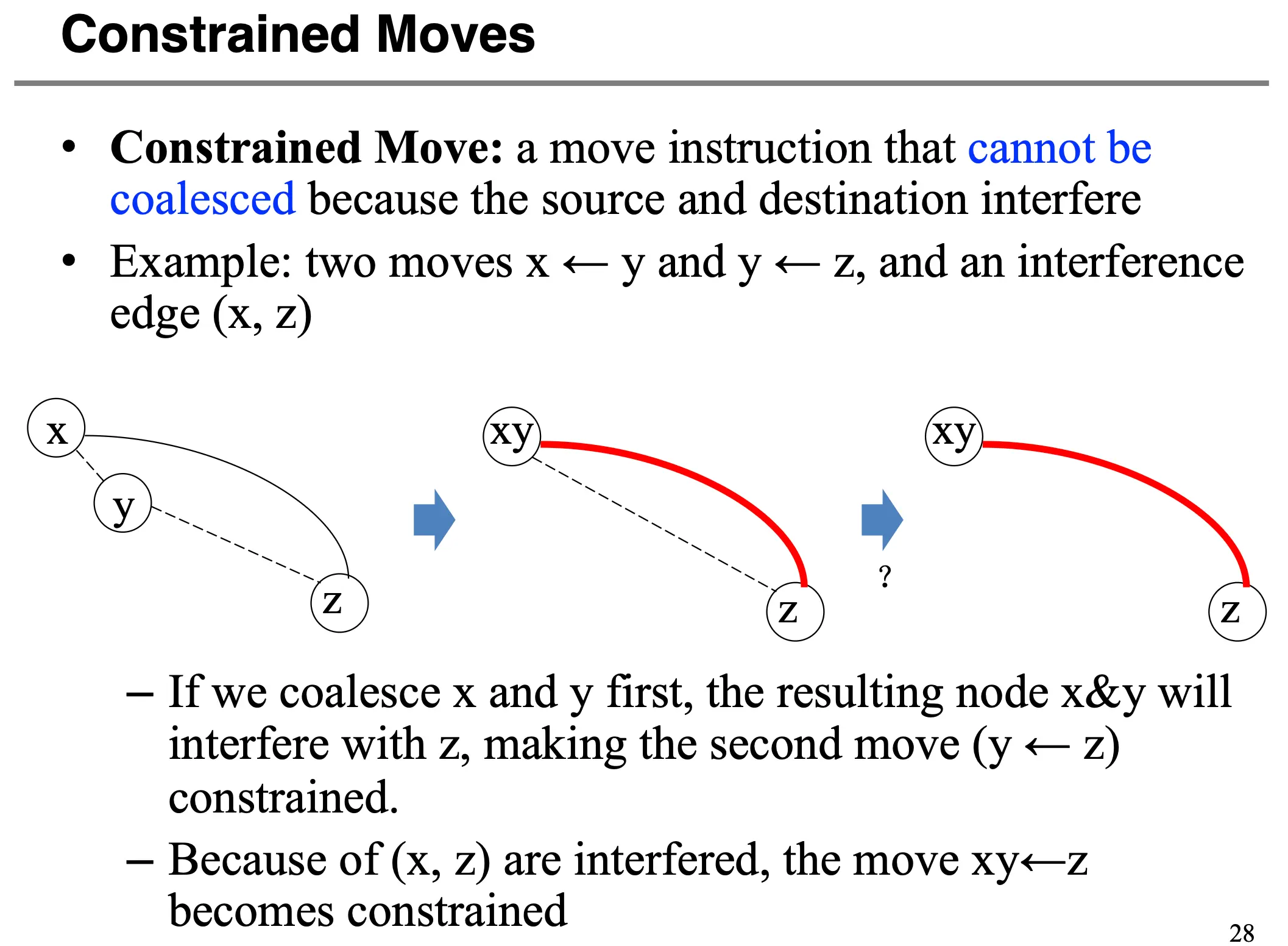
有时候合并会引入限制移动/Constrained Move，比如下面这个例子，这时候去掉虚线边就好了：

Constrained Move

3.4 预染色节点/Precolored Nodes

会有一些寄存器是不能通用的，比如栈指针 sp，帧指针 fp 等，调用惯例也限制了一些寄存器保存参数和返回值，一些操作也需要特殊的寄存器（比如 x86 的除法）。预染色可以将这些硬件要求直接融入到图染色的最终分配中，不生成错误的分配。

对于一个有 \(K\) 个物理寄存器的机器，就会有 \(K\) 个预染色节点，他们之间两两干涉，在简化阶段不能被简化，也不能被溢出到内存之中。我们可以给一个一般的临时值染一个和预染色寄存器相同的颜色，只要这个临时值不和这个预染色寄存器干涉。比如一些在调用惯例里出现的寄存器可以在函数内当作临时寄存器使用，这个临时值的颜色就是调用惯例要求的寄存器的颜色。

为了处理预染色节点：

  • 在构建干涉图的时候，将预染色节点也作为节点加入，并与所有活跃变量建立必要的干涉边；
  • 在简化阶段，绝不删除预染色节点，只对非预染色节点进行简化；
  • 在着色节点，尊重预染色节点已经分配到的颜色，不重新分配；
  • 当合并阶段和预染色节点相关的时候，我们一般使用 George 条件来判断是否可以合并；
  • 简化、合并、溢出将一直执行，直到只有预染色节点剩下来；
  • 由于预染色节点不能被溢出，前端必须保证预染色节点的活跃区间足够短，不然就会阻塞其他变量占用这些寄存器。

对于被调用者保存寄存器，保存的值一般跨函数调用，应当在函数的入口处将这些寄存器的值复制到临时值上，在函数的出口处再将这些临时值复制回寄存器，这样就将其活跃区间缩短到了只在复制点。对于调用者保存寄存器，在汇编层面，CALL 指令相当于定义了所有调用者保存寄存器，因此我们趋于将不需要跨越某个函数调用的变量保存到调用者保存寄存器中。

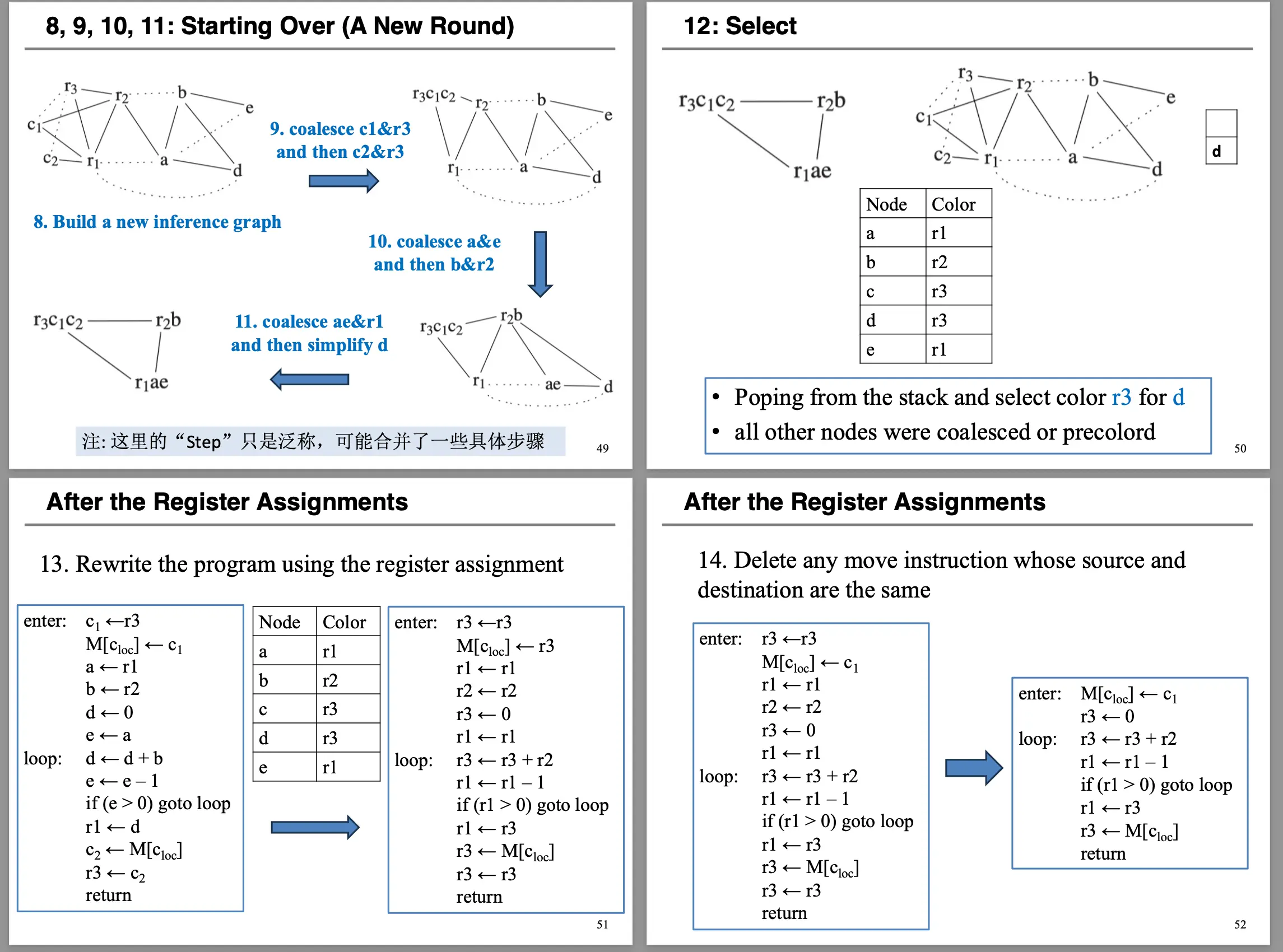
3.5 合而为一

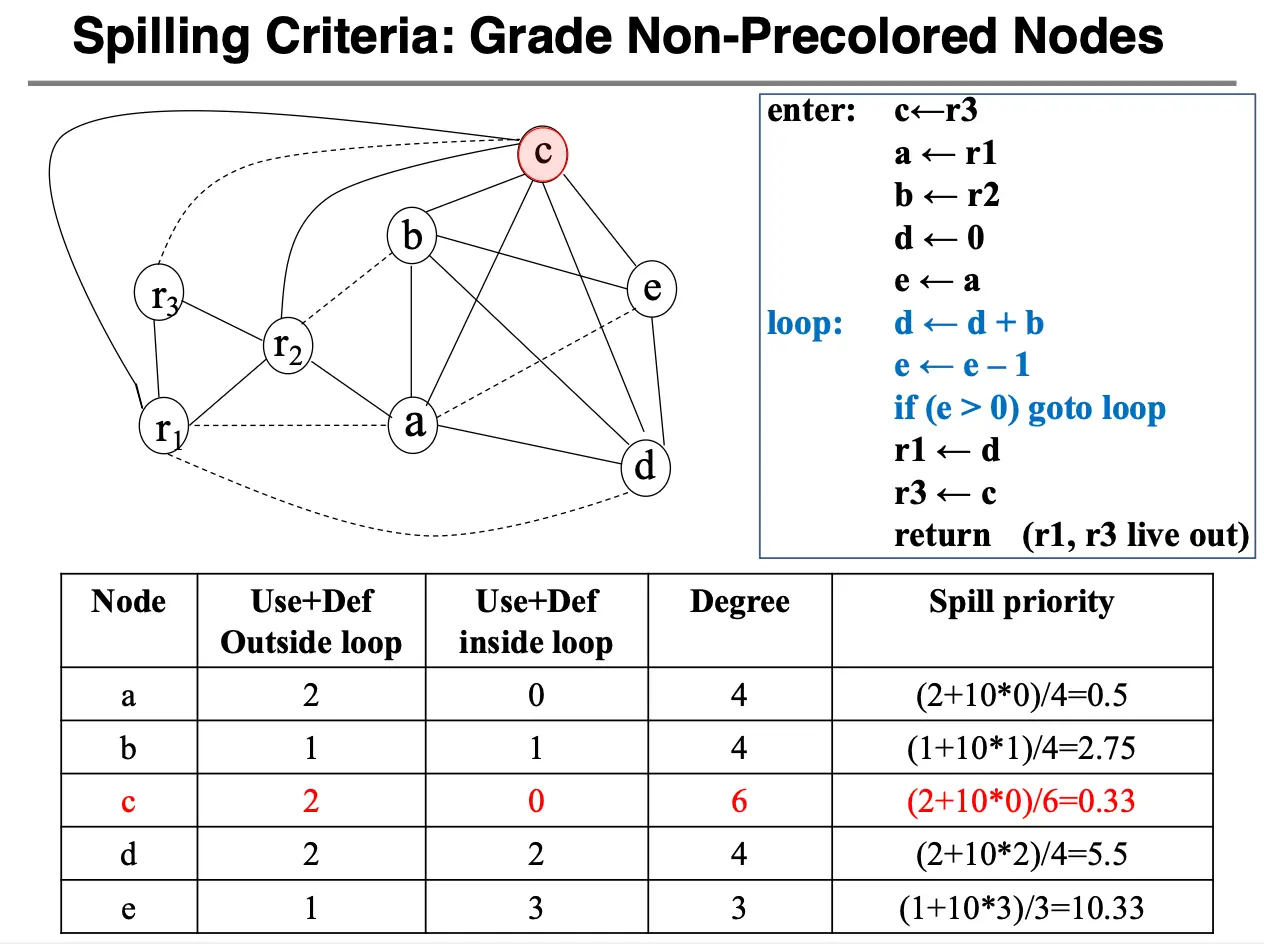
就是一个例子，但是很有学习价值：

Source Code

决定溢出 c，这里我们估计循环会执行 10 次，因此对循环内的使用和定义的优先级都乘以 10，溢出 c 是因为其度最高且使用次数最少。

First Process

First Process

First Process

Second Process