跳转至

Topic 4：语义分析

约 2860 个字 95 行代码 7 张图片 预计阅读时间 11 分钟

语义分析/Semantic Analysis 会将变量的定义与它们的各个使用联系起来，检查每一个表达式是否有正确的类型，并将抽象语法转换成更简单的、适合于生成机器代码的表示。广义地说，语义分析部分通过各种程序表示分析程序，一般包括控制流图/Control Flow Graph、静态单赋值/Static Single Assignment、程序依赖图/Program Dependence Graph 等。典型的语义分析任务包括类型检查/Type Checking、死代码消除/Dead Code Elimination，代码生成/Code Generation 等。

我们在编译原理课上一般讲的都是狭义的语义分析，包括通过抽象语法树确定一些静态属性，比如作用域与名字的可见性，变量、函数和表达式的类型检查。也将 AST 转化成中间代码，这在下下章节中会详细介绍。

Outline

1. 符号表

1.1 符号表的结构

  • Binding：给一个符号赋予含义，将类型、值等信息绑定到一个标识符上；
  • Environment：一个绑定的集合；
  • Symbol Table：环境的实现/The implement of environment。

语义分析的过程：按照特定顺序遍历抽象语法树，在此过程中维护一个符号表。

对于第四行，可以看见新引入了一个 Binding \(a \mapsto \mathrm{string}\)，覆盖了之前在 \(\sigma_2\) 中对 \(a\) 的 Binding，也就是说内层作用域的绑定会优于外层作用域的绑定。

当语义分析到达作用域的重点的时候，作用域内定义的标识符的绑定会被丢弃。在第六行，\(\sigma_2\) 和 \(\sigma_3\) 都会被丢弃。

在某些语言，可能在同时会有多个环境同时活跃，比如每一个模块/Module、每一个类/Class 都需要有自己的符号表。

1.2 符号表的实现

符号表需要实现下面这些接口：

  • 插入/Insert：将名称绑定到相关信息（如类型），如果名称已经在符号表中定义，那么新的绑定优先于旧的绑定；
  • 查找/Lookup：在符号表中查找特定名称绑定的信息；
  • 开始作用域/beginScope：进入一个新的作用域；
  • 结束作用域/endScope：退出作用域，降幅号表恢复到进入之前的状态。

符号表的实现主要有两种，命令式风格/Imperative Style 和函数式风格/Functional Style：

命令式风格的想法：有了新的就看不见老的，但是退出当前作用域的时候还得可以回得去。

  • 直接修改当前的符号表 \(\sigma_1\) 为 \(\sigma_2\)；
  • 当 \(\sigma_2\) 存在的时候，我们就不能查看 \(\sigma_1\) 中的内容；
  • 当我们退出当前作用域 \(\sigma_2\) 的时候，我们需要重做我们修改，将 \(\sigma_2\) 恢复为 \(\sigma_1\)。

函数式风格的想法：每次作用域/符号表发生变化的时候，都保留老的符号表。

  • 当创建新环境 \(\sigma_2\) 的时候，仍然保留老的环境 \(\sigma_1\) 不变；
  • 恢复老环境也很容易，直接丢了 \(\sigma_2\) 就行。

命令式符号表的实现策略主要有三：

  • 使用一个哈希表栈，每个作用域都有自己的哈希表，查找的时候从最近最新的作用域开始向前查找，很简单但是可能对内存不友好；
  • 使用一个单独的哈希表，加上作用域标记栈：哈希表用来存储所有符号，额外使用一个栈来标记作用域的边界，内存效率很高但是在退出作用域的时候需要清理。
  • 带名字修饰的扁平命名空间/Flat Namespace with Name Mangling：讲作用于的信息直接编码到符号名字内，不需要显式的作用域追踪了。

着重讲解第二种：

  • 使用一个哈希表存储所有作用域中的活动绑定，哈希表的每一个值其实被实现为一个栈；
  • 使用一个栈追踪哪些符号在哪些作用域内被添加；
  • 当新进入一个作用域的时候，需要向栈内压入一个特殊的标记；
  • 在添加一个符号的时候，我们将符号的绑定信息添加到哈希表中（压入到对应的栈中），并且将该符号记录在栈中；
  • 在退出作用域的时候，我们从栈顶不断弹出符号，并且在哈希表中删除对应的绑定，直到遇到作用域标记，最后将该标记也弹出栈。
姚老师使用 Python 的实现 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from dataclasses import dataclass
from typing import TypeVar, Generic, Optional

T = TypeVar('T')

@dataclass
class ScopeMarker:
    """标记作用域的开始"""
    pass

class SymbolTable:
    def __init__(self):
        self.stack = []
        self.bindings = {}

    def add(self, identifier: str, value: T):
        """添加新的绑定到当前作用域"""
        self.stack.append(identifier)
        self.bindings[identifier] = self.bindings.get(identifier, []) + [value]

    def lookup(self, identifier: str) -> Optional[T]:
        """查找标识符的最新绑定"""
        if identifier in self.bindings and self.bindings[identifier]:
            return self.bindings[identifier][-1]
        return None

    def begin_scope(self):
        """开始一个新的作用域"""
        self.stack.append(ScopeMarker())

    def end_scope(self):
        while len(self.stack) > 0 and not isinstance(self.stack[-1], ScopeMarker):
            identifier = self.stack.pop()
            self.bindings[identifier].pop()

        if not self.bindings[identifier]:
            self.bindings.pop(identifier)

        if self.stack:
            self.stack.pop()

函数式符号表的基本思想是：在实现添加绑定操作的时候，不是直接修改 \(\sigma_1\)，而是创建一个新的符号表 \(\sigma_2\)。当退出作用域需要删除绑定的时候，只需要简单的恢复旧的符号表就可以，方便了快速回退。

典型的函数式符号表使用二叉搜索树实现，每一个节点都包含着从标识符（键）到绑定值（值）的映射，使用字符串比较确定键之间的序关系。这样的话，查找遵循标准的 BST 搜索算法，插入需要按照 Persistent BST 的插入实现，使用路径复制技术，赋值从根节点到被插入节点的父节点的所有节点：

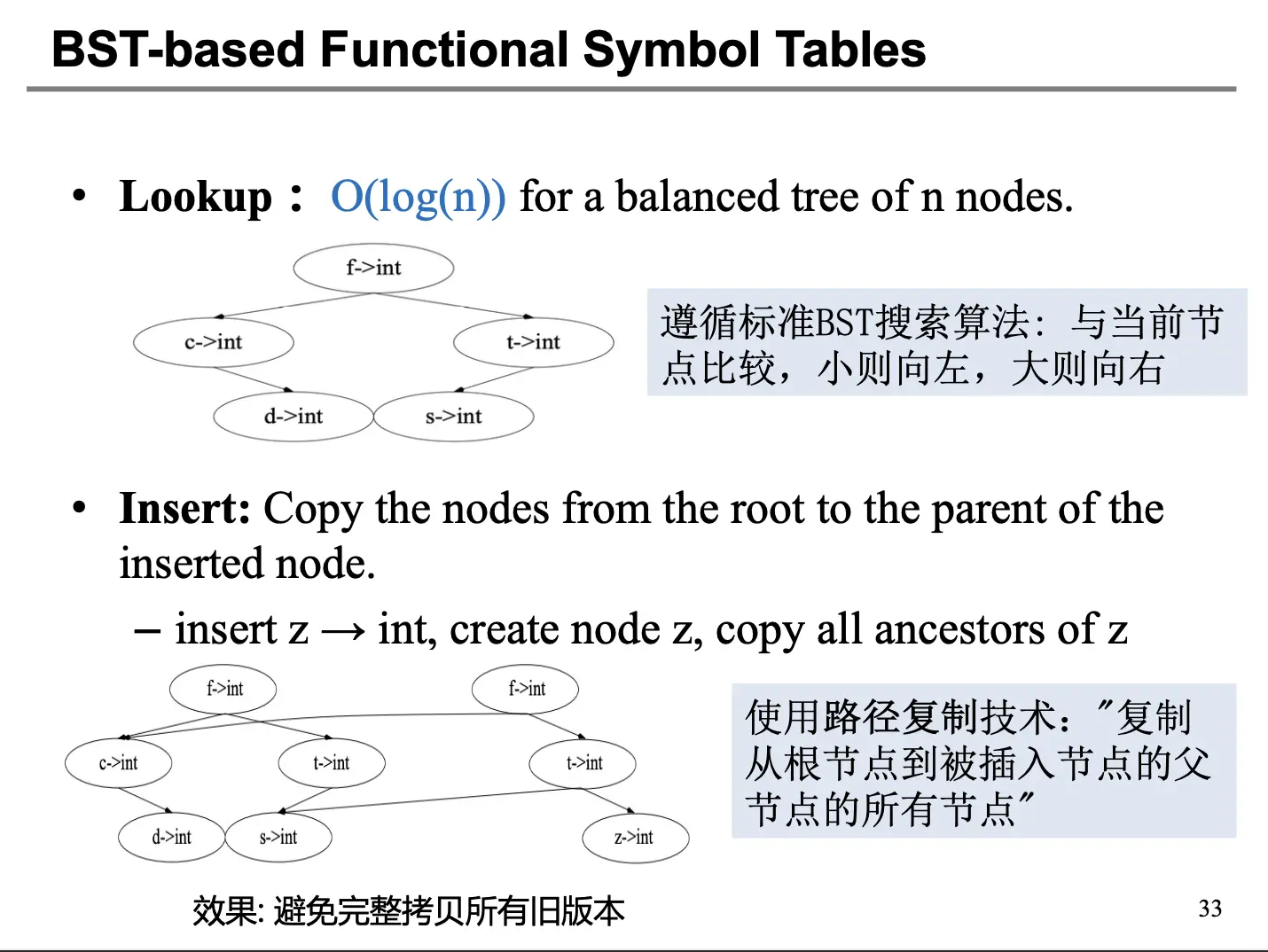
简单总结一下：

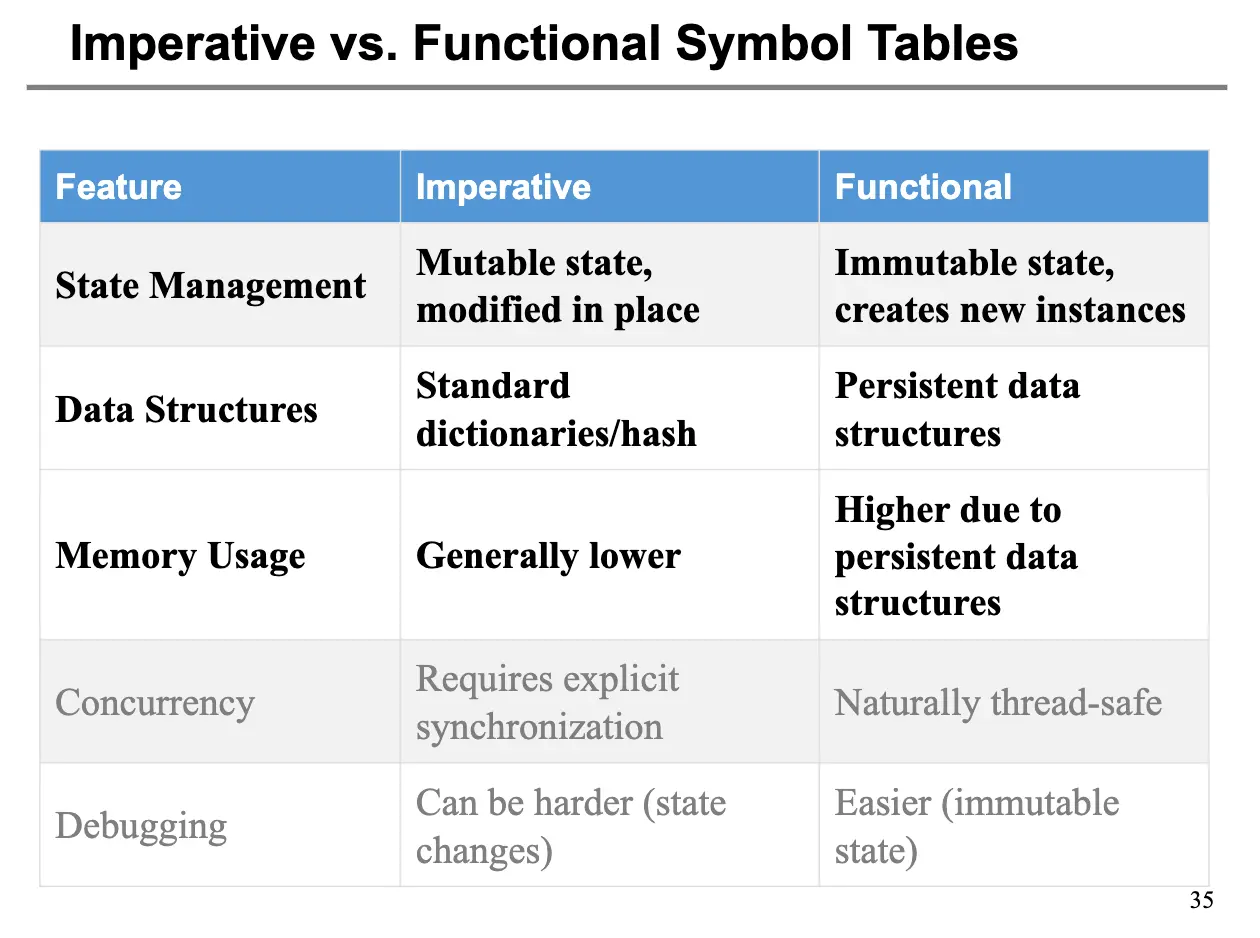
  • 命令式风格的符号表存在副作用，当进入新的作用域的时候，通过副作用直接修改符号表，破坏了旧的符号表，另外，需要额外的信息来移除新加入的绑定，重建旧的符号表。
  • 函数式风格的符号表不存在副作用，当每次进入新的作用域的时候，都会通过在旧表上添加信息来创建新的环境，旧表保持完整。当退出作用域的时候，简单取回旧表的引用即可，如果我们使用平衡树实现，访问和插入的时间复杂度都为 \(O(\log N)\)。

2. 类型检查

2.1 类型及其作用

一个表达式的类型告诉我们这个表达式可以表示哪些值，以及对这些值可以执行哪些操作。类型系统/Type System 定义了什么是良构类型/Well-formed Type，并且包含了一套类型规则。

类型检查确保了程序中的操作都按照类型系统的规则被正确地应用。可以将类型检查分为静态/Static 和动态/Dynamic 两种：分别在编译期和运行期进行。

  • Soundness：如果类型系统接受一个程序，那么这个程序在运行时就不会出现类型错误，「Well-typed programs don't go wrong」；
  • Completeness：如果一个程序在运行时不会出现类型错误，那么类型系统一定接受这个程序。

类型检查主要的议题有：

  • 哪些是合法的类型？比如 int，string，nil 都是合法的；
  • 如何定义两个类型是等价的，比如两个 record 类型都是等价的；
  • 什么是类型规则？
  • 在源代码之中需要指定多少类型信息，比如类似于 ML 这样的隐式类型/Implicitly-Typed 语言需要使用类型推断。

2.2 Tiger 类型系统

  • 基本类型/Primitive Type：int，string；
  • 构造类型/Constructed Type：record（其实就是结构体），array；
  • 命名类型/Named Type：用户通过类型声明定义的类型，可以参照文法；
  • NIL 类型：记录类型的特殊类型。
\[\begin{aligned} \mathrm{typec} & \rightarrow \mathbf{type}\ \mathrm{type\_id} = \mathrm{ty} \\ \mathrm{ty} & \rightarrow \mathrm{type\_id} \\ & \rightarrow \text{\{} \mathrm{tyfields} \text{\}} \\ & \rightarrow \mathbf{array}\ \mathbf{of}\ \mathrm{type\_id} \\ \mathrm{tyfields} & \rightarrow \varepsilon \\ & \rightarrow \mathrm{id}\text{: } \mathrm{type\_id}\ \{ \text{, } \mathrm{id}\text{: } \mathrm{type\_id} \} \end{aligned}\]

类型等价性/Type Equivalence：

  • 命名等价性/Named Equivalence/NE：两个类型指向同一个类型声明定义的相同类型标识符；
  • 结构等价性/Structural Equivalence/SE：两个类型的内部结构一样，也就是以相同的构造器按照相同的顺序组合而成。
1
2
type t4 = {x:int; y:int}
type t5 = {x:int; y:int}

比如上面两种类型就是 SE 的，但是不是 NE 的。Tiger 使用命名等价性，每一个新的字面量记录类型表达式/Record type Expression 都会创建一个一个新的/也是不一样的 Record type。

Tiger 允许定义类型别名/Type Alias，在命名等价性下，类型别名和它们指向的类型是等价的。

1
2
3
4
5
6
let type a = {x: int; y: int}
    type b = a
    var i: a := a {x=1, y=2}
    var j: b := a {x=3, y=4}
in i := j                
end

除此之外，Tiger 还不允许隐式类型转换；所有变量必须在声明的时候被初始化。在函数调用的时候，形式参数的类型必须和实参的类型完全匹配。数组下标一定是整数类型。NIL 类型属于所有记录类型，并且等价于所有记录类型，表达式 nil 具有 NIL 类型。

允许通过记录和数组定义递归类型：

1
2
type list = {value: int; next: ListRef}
type ListRef = array of list

在一级相互递归的类型定义中，任何递归循环都必须经过至少一个 record 或者 array 类型构造器，不允许只经过类型别名形成循环。

1
2
type a = b
type b = {i: a}

同时，Tiger 有两个不同的命名空间，类型名和变量/函数名是分开的。

2.3 Tiger 类型检查：Formalization

类型语境/Typing Context：我们将符号表写成 \(\Gamma\)，\(\Gamma = x_1: \tau_1, x_2: \tau_2, \cdots, x_n: \tau_n\)。

类型判断/Typing Judgement：\(\Gamma \vdash e : \tau\) 表示表达式 \(e\) 的类型是 \(\tau\)；

类型规则/Typing Rules：每一个类型规则都形如 \(\dfrac{\mathrm{premise1}, \mathrm{premise2}, \cdots}{\mathrm{conclusion}}\)，表示如果前提成立，那么结论成立。

2.4 Tiger 类型检查：Type Checking

对于 Tiger 来讲，类型检查需要维护两个主要的环境（本质上是符号表）：

  • 类型环境/Type Environment：把类型符号映射到其表示的具体类型对应的数据结构；
  • 值环境/Value Environment：存储变量名称到其类型的映射和函数名称到参数类型和返回值类型的映射。

类型检查组合地实现下面几件事：

  • 将复杂的表达式分解为其他直接的子表达式；
  • 对每一个子表达式递归的进行类型检查，确定其类型；
  • 确保顶级表达式本身可以被类型检查，并且类型正确。

在整个过程中，通过维护环境来记录/查找变量或者函数的类型。

每一个类型规则都对应着类型检查器的一部分：

类型检查本质上其实是对抽象语法树递归的遍历，处理每一个节点的时候，执行下面步骤：

  • 检查当前节点的类型；
  • 递归检查当前节点的子节点；
  • 根据当前节点检查得到的类型和子节点检查得到的类型，应用合适的类型规则；
  • 检查类型是否兼容，如果发现类型错误，则报告错误。

尽管我们是自顶向下地遍历抽象语法树，类型信息从底向上进行传播。

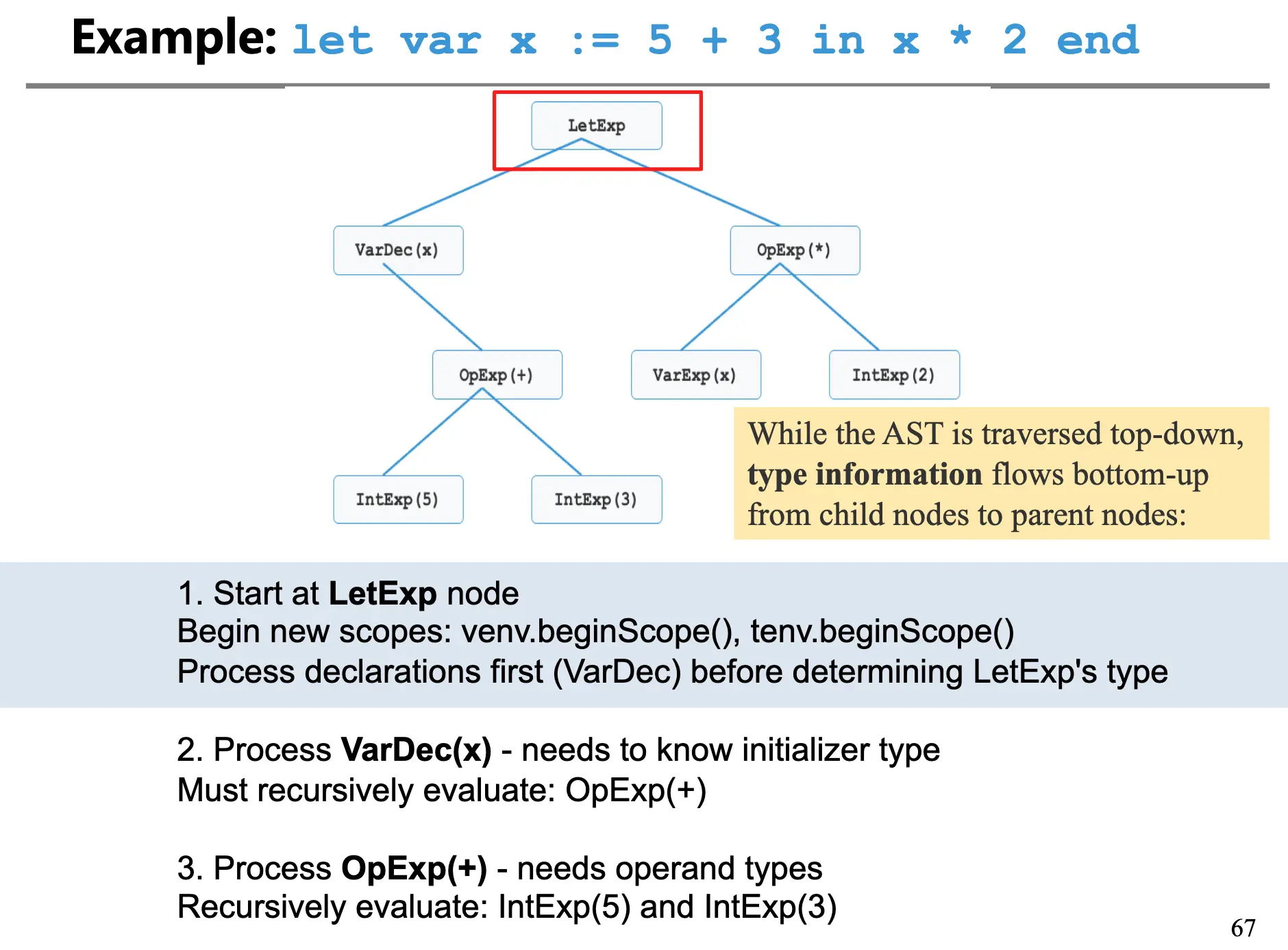
现实世界的类型系统复杂的多，举几个很坑爹的例子：

  • 互递归函数/Mutually Recursive Functions：Functions that call each other；

    1
2
3
4
5
    (* Check if a non-negative integer is even *)
let rec is_even n = if n = 0 then true else is_odd (n - 1)

(* Check if a non-negative integer is odd *)
and is_odd n = if n = 0 then false else is_even (n - 1)

  • 多态/Polymorphism：Generic types and functions；

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
    (* 定义一个交换元组元素的函数 *)
(* 'a 和 'b 是类型变量，代表任意类型 *)
let swap (x : 'a) (y : 'b) : ('b * 'a) = (y, x)

(* 使用不同类型的元组调用 swap *)
let () =
    let pair_integer = (1, 2) in
    let swapped_integer = swap (fst pair_integer) (snd pair_integer) in
    Printf.printf "Swapped (%d, %d) -> (%d, %d)\n" (fst pair_integer) (snd pair_integer) (fst swapped_integer) (snd swapped_integer);

    let pair_string_float = ("hello", 3.14) in
    let swapped_string_float = swap (fst pair_string_float) (snd pair_string_float) in
    Printf.printf "Swapped (%s, %.2f) -> (%.2f, %s)\n" (fst pair_string_float) (snd pair_string_float) (fst swapped_string_float) (snd swapped_string_float);

  • 子类型/Subtyping：Type hierarchies and inheritance；

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
    (* 定义基类 animal *)
class animal (name : string) = object (self)
    val name = name
    method get_name = name
    method make_sound = "..."
end

(* 定义子类 dog，继承自 animal *)
class dog (name : string) = object (self)
    inherit animal name
    method! make_sound = "Woof!"  (* 覆盖父类方法 *)
    method wag_tail = true       (* 新增的方法 *)
end

(* 子类型多态使用示例 *)
let () =
    let a = new animal "Generic" in
    let d = new dog "Buddy" in

    (* 上行转换: dog 可以被视为 animal *)
    let animals = [a; (d :> animal)] in

    List.iter (fun a -> 
        Printf.printf "%s says %s\n" a#get_name a#make_sound
    ) animals