Topic 13:循环优化¶
约 1959 个字 8 行代码 17 张图片 预计阅读时间 7 分钟
Outline
- 1. 循环与支配节点
- 2. 循环不变量外提
- 3. 归纳变量 「很遗憾,不考了」
- 4. 循环展开 「很遗憾,不考了」
- 5. 数组边界检查 「很遗憾,你也不考」
循环无处不在,程序几乎大部分执行时间都花在循环体里,因此优化循环可以显著提升程序性能,衍生出了很多循环优化技术,比如:循环不变量外提/Loop Invariant Hoisting、归纳变量简化/Induction Variable Reduction、循环展开/Loop Unrolling、循环融合/Loop Fusion、循环分裂/Loop Fission、循环互换/Loop Interchange、循环剥离/Loop Peeling、循环分块/Loop Tiling 等等,有些我们在体系结构课程结合流水线和缓存局部性原理讲过,有的还是第一次讲。举一个循环不变量外提的例子:
t = a + b 每次迭代都重复计算但实际上不变,标记它为循环不变式。显然提出来会提升性能。
1. 循环与支配节点¶
在控制流图中,循环是带有一个头节点 \(h\) 的一个节点集合 \(S\),且满足以下条件:
- 从 \(S\) 中任意节点到 \(h\) 存在一条有向路径;
- 从 \(h\) 到 \(S\) 中任意节点有路径;
- 除 \(h\) 之外,\(S\) 内其他节点不允许有来自 \(S\) 外的入边。
下面这个图就不是一个循环,虽然带着一个圈。
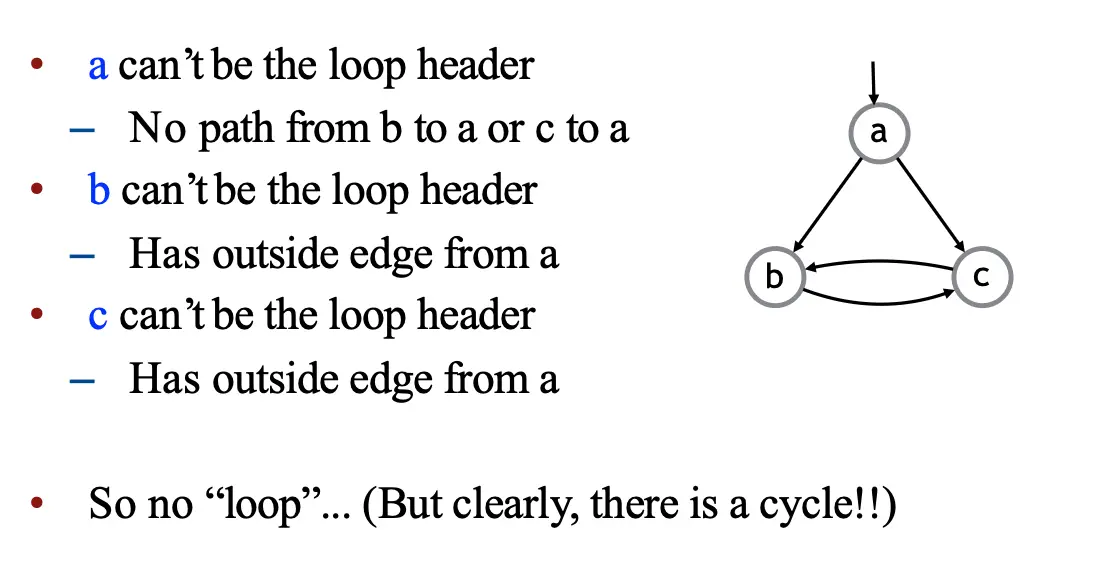
这样的循环定义和词典定义略有不同,这是特别为了编译优化准备的。为什么这么定义?循环头相当于提供了一个处理循环的 handle,结构化的控制流也只会产生可约图,很多分析和循环优化也依赖可约图性质。
- 循环入口/Loop Entry:是集合 \(S\) 内带有循环外的前驱节点的节点,由于定义,循环入口唯一,一定是头节点 \(h\);
- 循环出口/Loop Exit:是集合 \(S\) 内带有循环外的后继节点的节点,循环出口可能不止一个;
支配点/Dominator:在控制流图中,一个节点 \(d\) 支配 \(n\) 当且仅当所有从入口 \(s_0\) 到 \(n\) 的路径都经过 \(d\)。

支配点有以下性质:每一个节点都支配自己;除了入口节点,所有节点都可以有多于一个支配点。令 \(\operatorname*{D}[n]\) 表示 \(n\) 的支配点集合,则有:
计算支配节点的算法如下:首先假定除了入口节点的支配点是全图节点集合,然后迭代更新,直至达到不动点。

直接支配节点/Immediate Dominator:除了入口节点,每一个节点 \(n\) 有且仅有一个直接支配节点 \(\operatorname*{idom}(n)\),满足:
- \(\operatorname*{idom}(n) \neq n\),且 \(\operatorname*{idom}(n) \in \operatorname*{D}[n]\);
- 在 \(n\) 的所有支配点中,\(\operatorname*{idom}(n)\) 不支配其他支配节点。
也就是,\(\operatorname*{idom}(n)\) 从入口节点到达 \(n\) 的任何路径中,最后一个支配 \(n\) 的节点。
第二个陈述基于下面定理:假设 \(d\) 和 \(e\) 都支配 \(n\),则 \(d\) 和 \(e\) 之间也有支配关系,即 \(d\) 支配 \(e\) 或 \(e\) 支配 \(d\)。
基于支配节点和直接支配节点的定义,我们可以构建一棵支配树,其根为入口节点,每个节点的父亲为直接支配节点,祖先是其所有支配节点。
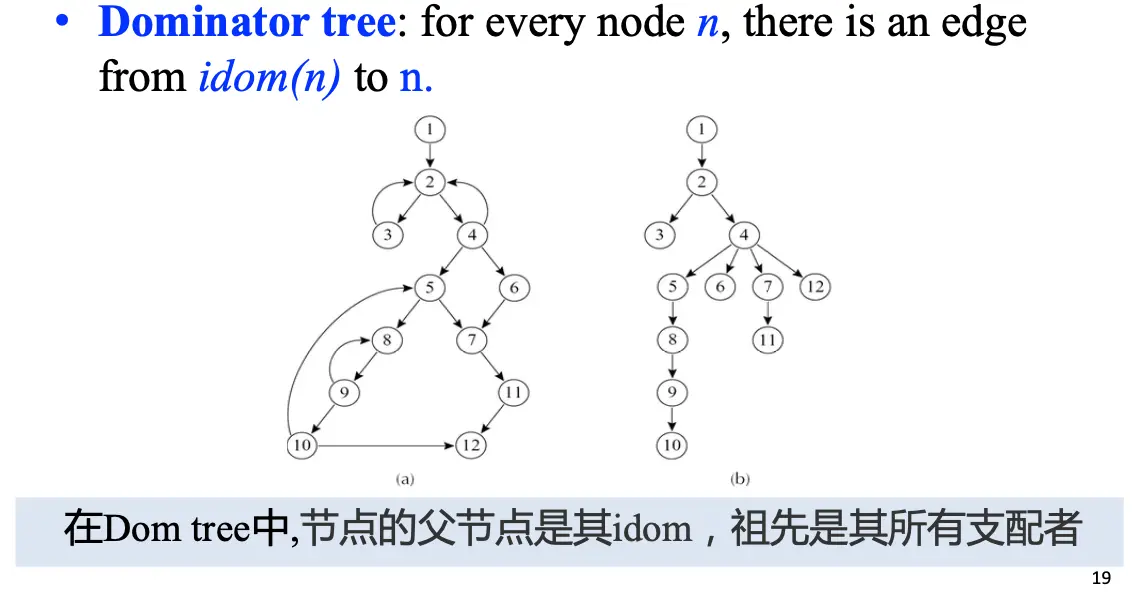
- 回边/Back Edge:从 \(n\) 到 \(h\) 的边,且满足 \(h\) 支配 \(n\)。在循环中,回边是循环头到循环入口的边。
- 回边 \(n \to h\) 对应的自然循环/Natural Loop:为一组节点 \(x\) 满足:\(h\) 支配所有 \(x\),且存在从 \(x\) 到 \(n\) 的不包含 \(h\) 的路径。
- 自然循环有唯一的入口节点/Header/首节点,入口节点支配循环中的所有节点,循环中至少有一条返回首节点的路径。
- 循环显然可以嵌套。

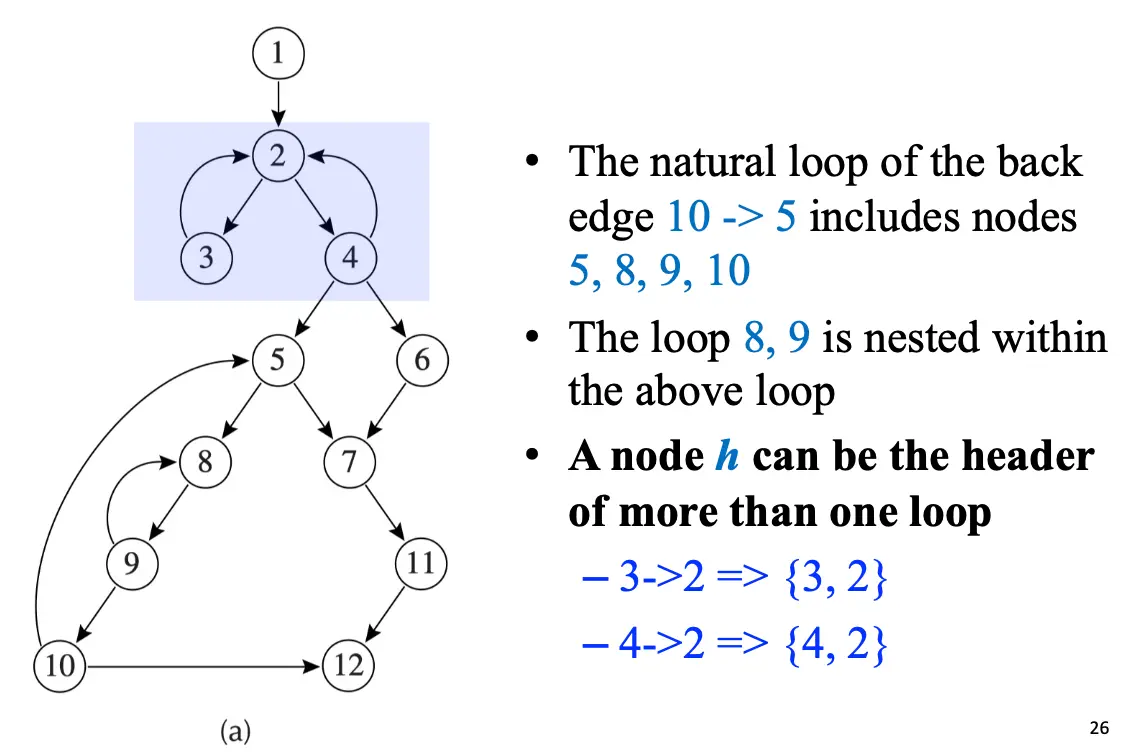
如果两个循环 \(A\) 和 \(B\) 有不同的首节点,且 \(B\) 的所有节点都在 \(A\) 内,那么我们说 \(B\) 嵌套在循环 \(A\) 内,\(B\) 是一个内层循环/Inner Loop。如果某个循环不包含别的循环,那么这个循环一个最内循环/Innermost Loop。
定理:除非两个自然循环的首节点相同,否则这两个循环要么互不相交,要么一个循环完全包含另一个循环。
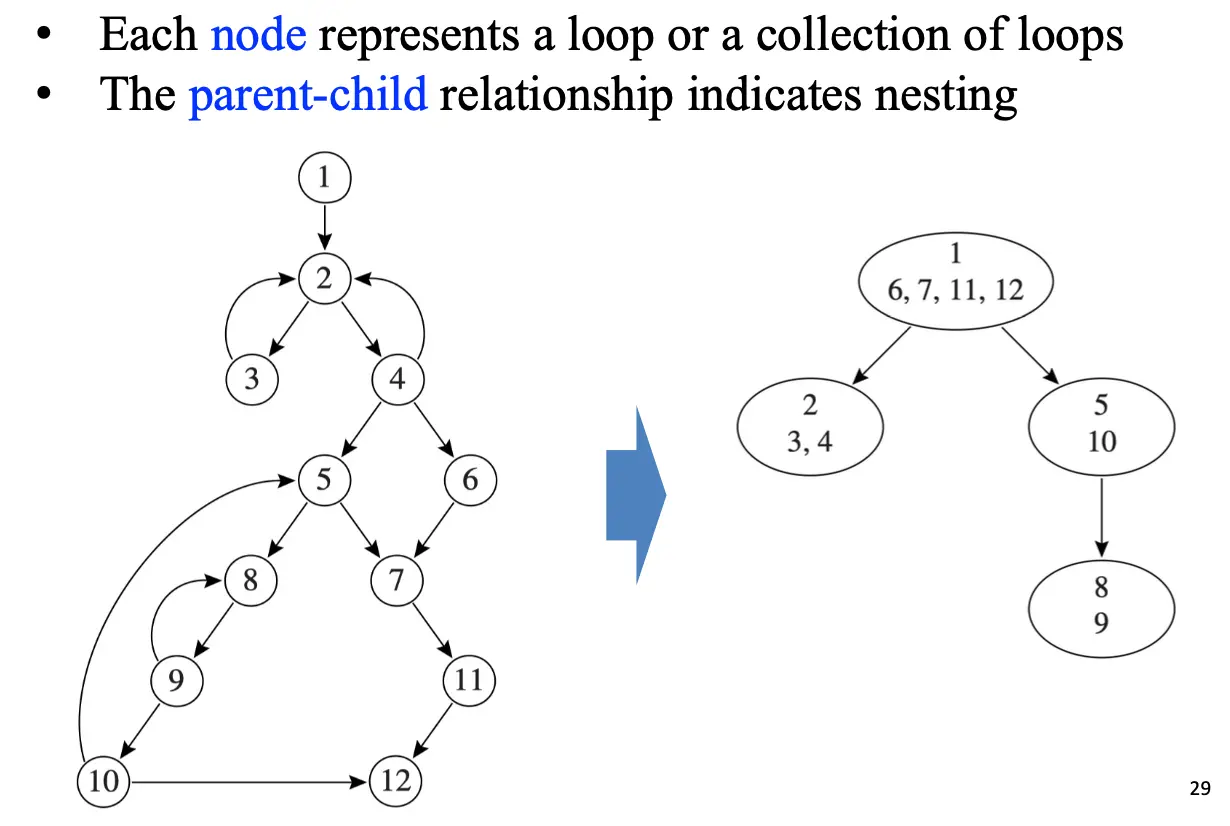
根据循环的嵌套关系,我们可以构建出一个循环嵌套树:
- 计算出图中的所有支配节点,构建出支配树,确定所有自然循环和循环头节点;
- 对于每一个循环头 \(h\),将 \(h\) 对应的所有的自然循环都合并为 \(\operatorname*{loop}[h]\);
- 构建循环头的树,这个树的结构如下定义:如果 \(h_1\) 是 \(h_2\) 的祖先,那么 \(h_2\) 一定在 \(\operatorname*{loop}[h_1]\) 内。
- 这样每一个节点都代表一个循环或者循环的集合;
- 节点的父子关系代表着嵌套关系。
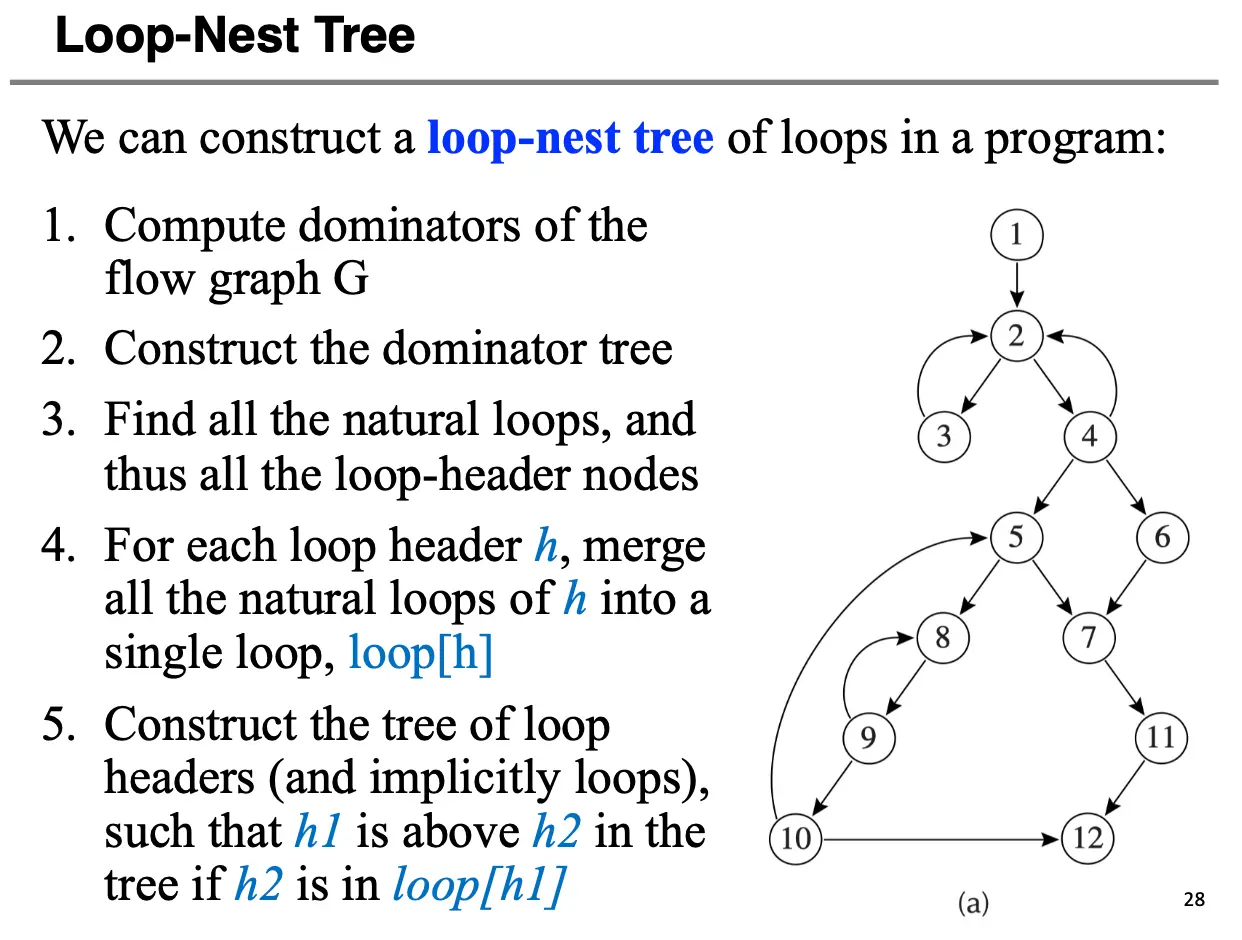
- 每一个循环头都在每一个椭圆节点的上侧;
- 树的叶子节点都是最内循环;
- 我们认为整个程序是一个伪循环/Pseudo-loop,因此程序的入口节点 \(s_0\) 在根节点的上侧,所有不包含在任何一个循环内的节点都在根节点的下半部分。
很多循环优化会在进入循环之前进行一些准备工作,也就是插入一个基本块作为循环头的前驱节点,这个基本块称为循环的前置首节点/Loop Preheader。需要满足:
- 前置首节点的唯一后继节点是循环头;
- 前置首节点是循环头的直接支配节点,也就是所有通向循环首节点的路径都经过前置首节点。
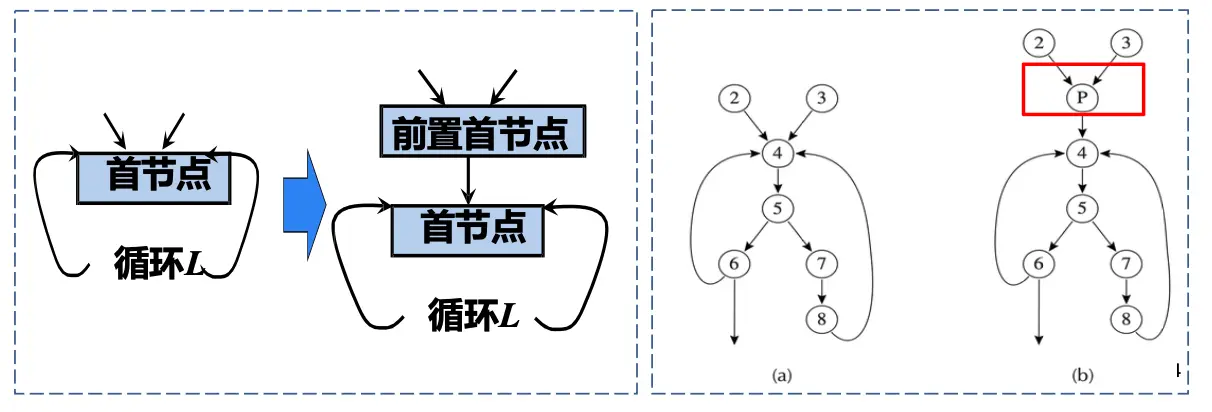
前置首节点就是循环不变量外提的目的地。
2. 循环不变量外提¶
2.1 循环不变量¶
主要想法:有一些在循环内求值的表达式从未改变过,这些表达式就是循环不变量/Loop Invariant。将其移出循环体,在循环外求值并存储在临时值之中,在每次迭代都使用临时值,可以提升性能。分两步:
- 分析/Analysis:在循环内找到不变量,特征为每次求值都计算相同的内容;
- 变换/Transformation:将循环不变量移出循环体。
对于一个赋值 x = v1 op v2,循环不变量有以下特征:对于每一个操作数 v1 和 v2,只有下面三种可能:操作数是常数、所有到达 x 的 v1 的定值都在循环之外、v1 只有一个定值到达 x,且该定值是循环不变量。

可以递归检查一个量是否是循环不变量。
2.2 循环不变量外提¶
循环不变量也不能完全直接外提,下面这个是直接外提安全的情况:

但是下面这个情况就不行,因为外提影响了语义:

我们引入可以安全外提的判别法:对于形如 d: t = a op b 的赋值语句,当且仅当满足以下条件时可以安全外提:
- 支配条件:\(d\) 必须支配所有 \(t\) 在其上 live-out 的循环出口;
- 唯一性条件:在循环中 \(t\) 只能有唯一的定义;
- 活跃性条件:\(t\) 不属于前置首节点的 live-out 集合;换句话说,\(t\) 在进入循环前不是活跃的。(第一次循环使用的是旧值)




