Part 5: Lecture 19 to Lecture 25¶
约 4783 个字 14 张图片 预计阅读时间 16 分钟
Table of Contents
Lecture 19: Generative Models I¶
首先我们区分监督学习/Supervised Learning 和 无监督学习/Unsupervised Learning 两种范式:
- 监督学习:接受的数据为 \((x, y)\),x 是输入、y 是标签,目标是学习一个函数 \(f: x \to y\),给定输入预测标签。典型的例子有:分类/Classification、回归/Regression、物体检测/Object Detection、语义分割/Semantic Segmentation、图像描述/Image Captioning 等等。
- 无监督学习:接受的数据只有 \(x\),目标是学习到数据的潜在结构。典型的例子有:聚类/Clustering、降维/Dimensionality Reduction、特征学习/Feature Learning、自编码器/Autoencoders、密度估计/Density Estimation 等等。
监督学习和无监督学习的区别在于数据是否有标签标注,生成模型是实现无监督学习、学习数据潜在结构的一种重要方法。下面我们可以根据使用的潜在概率结构的模型分为三类:
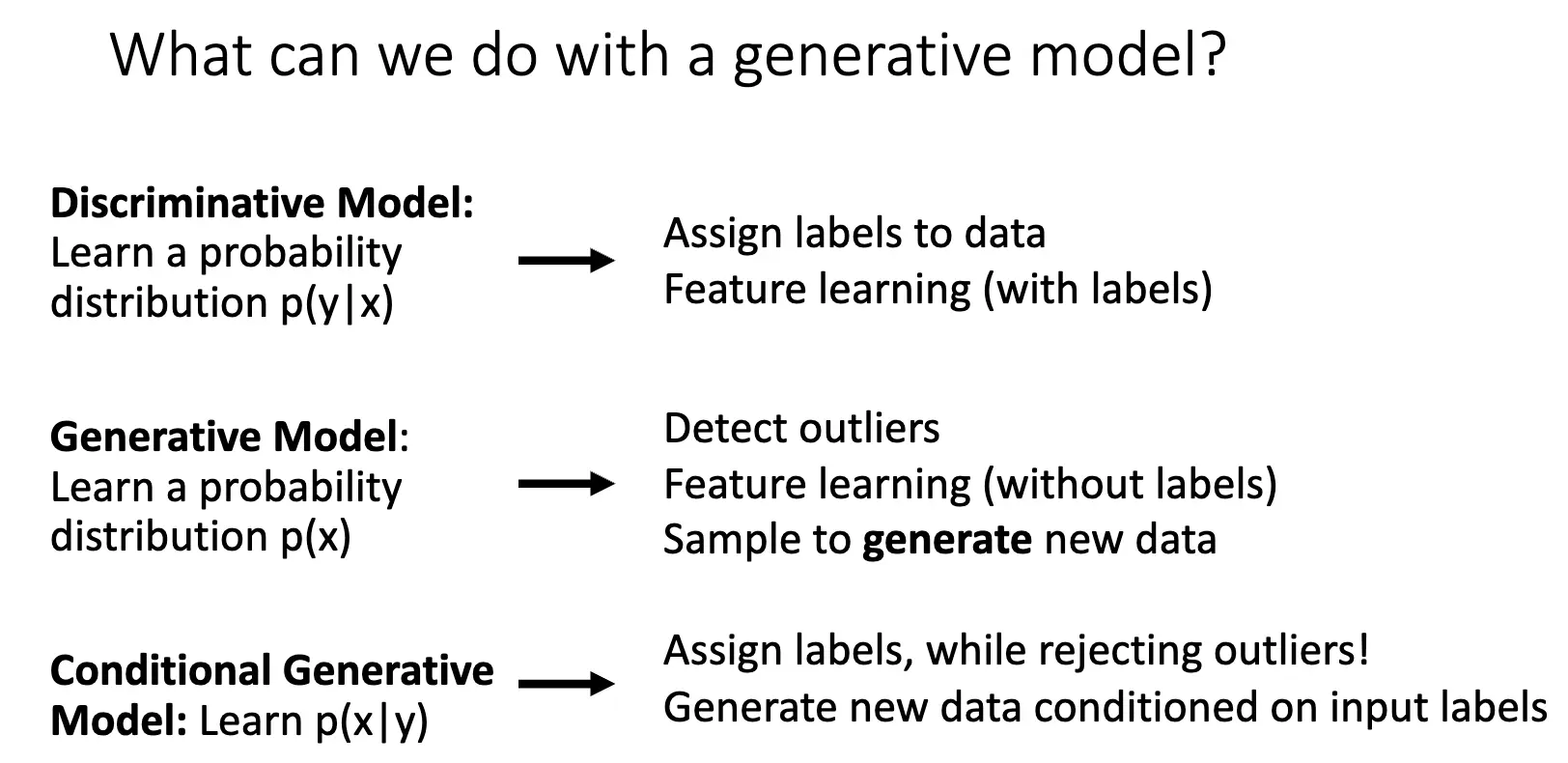
- 判别模型/Discriminative Model:学习条件概率分布 \(p(y \mid x)\),给定输入 \(x\) 预测标签 \(y\)。由于 \(\displaystyle \int_y p (y \mid x)\, \mathrm{d}y = 1\),对于一个输入,其可能的标签类别会互相竞争。但是判别模型无法拒绝不合理的输入,比如我们的标签只有猫和狗,但是输入是一个猴子的图片,模型仍然会强行给出一个分类结果,而无法拒绝这个输入。
- 生成模型/Generative Model:学习数据的分布 \(p(x)\),给定一个输入 \(x\),输出这个输入发生的概率,这意味着生成模型对输入进行建模,这就要求模型必须深入理解视觉信息和潜在结构。生成模型内所有的可能输入会相互竞争,合理的输入会被分配高概率,而不合理的输入会被分配低概率,因此生成模型可以拒绝不合理的输入。注意到生成模型实际上对输入进行建模,实际上我们可以通过从 \(p(x)\) 中采样来生成新的数据。
- 条件生成模型/Conditional Generative Model:学习条件概率分布 \(p(x \mid y)\),给定标签 \(y\),输出符合该标签的输入 \(x\) 的概率分布,比如给定标签猫,生成模型建模输入为猫的图像分布。回忆贝叶斯法则:\(p(x \mid y) = \dfrac{p(y \mid x)}{p(y)} p(x)\),我们可以使用生成模型、判别模型和标签的先验概率 \(p(y)\) 来构建条件生成模型。
本节讨论生成模型,生成模型可以按照是否能够显式计算出数据的概率分布 \(p(x)\) 来分类:Autoregressive Models 可以显式计算出 \(p(x)\) 的具体数值,另一种是计算出 \(p(x)\) 的近似值,如果使用变分推断,那么就得到了变分自编码器/Variational Autoencoder/VAE,如果使用马尔可夫链方法,那我们就得到了玻尔兹曼机/Boltzmann Machine;另一种类型是不直接计算出 \(p(x)\),而是通过采样来生成数据,比如生成对抗网络/Generative Adversarial Networks/GANs。
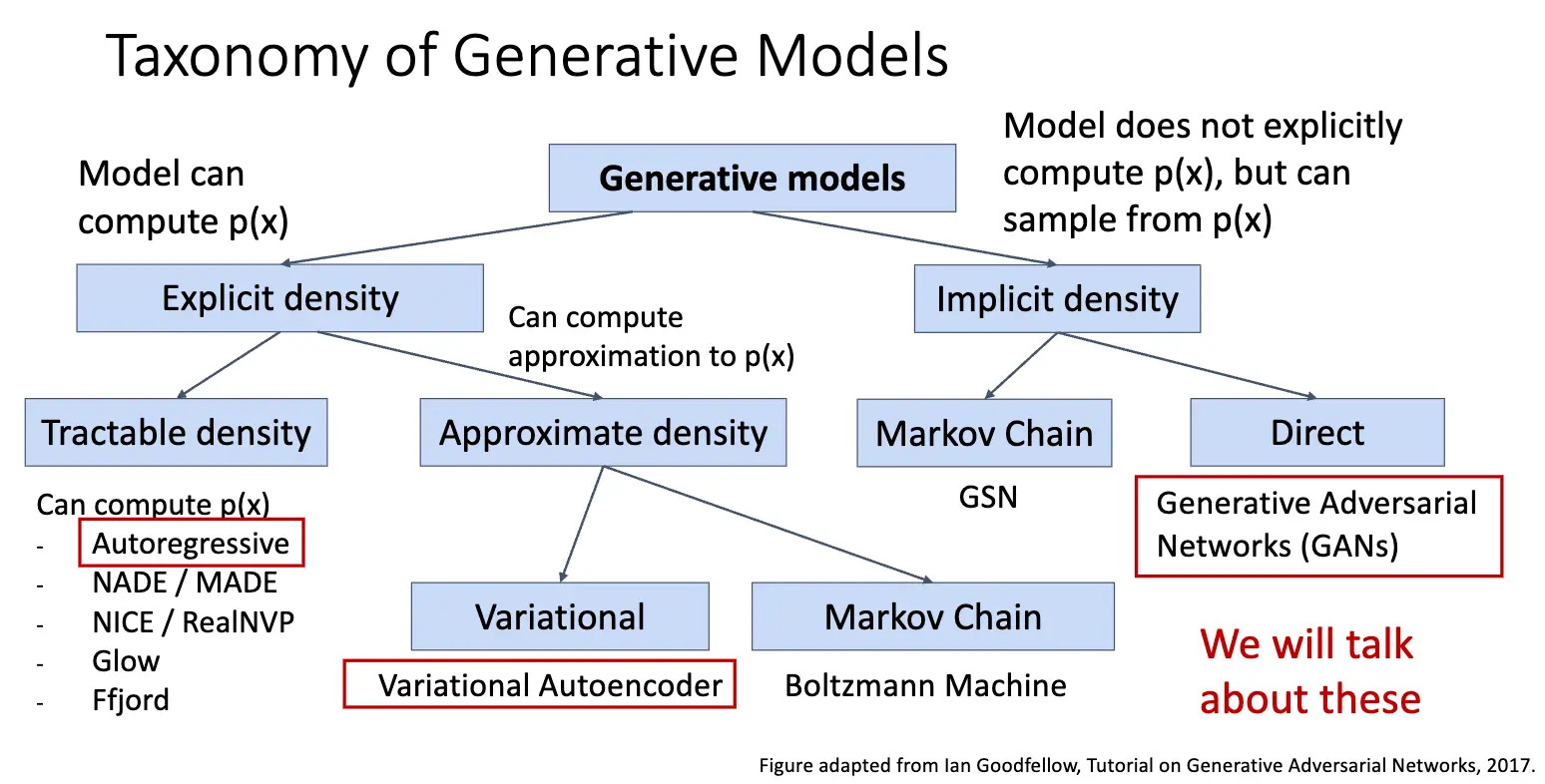
本节我们主要讨论 Autoregressive Models 和 VAE,下一节是 GAN 的内容。
自回归模型/Autoregressive Models 的目标是直接建模数据的概率分布 \(p(x) = f(x, W)\),其中 \(x\) 是输入数据,\(W\) 是模型的参数,对于一系列的训练数据 \(x^{(1)}, x^{(2)}, \ldots, x^{(N)}\),使用最大似然估计/Maximum Likelihood Estimation/MLE 来训练模型,寻找一个可以以最大的概率输出训练数据的参数集合:
最后一行就是我们优化的目标,令 \(f\) 为参数为 \(W\) 的神经网络,我们使用梯度方法来优化它。
假设 \(x\) 由不同部分组成——这是比较符合逻辑的,比如图像由像素组成,文本由单词组成,我们可以将 \(x\) 看作一个序列 \((x_1, x_2, \ldots, x_T)\),使用概率的链式法则/Chain Rule 将联合概率分解为条件概率的乘积:

这个式子的基石是整个内容的下一部分在某种意义上依赖于前面内容的假设/事实,将图像生成问题转化成了一个预测问题,每一次只需要预测下一个像素是什么就可以,而自回归的名字就来源于此,模型通过预测/回归自身的历史部分来定义整个分布。我们使用 RNN 来进行建模,这就是 PixelRNN。

PixelRNN 从左上角的像素开始生成图像,一点一点向外扩展,每次生成一些像素,生成当前像素的时候,依赖于它左边和上边的像素,这样每一次生成的像素都隐式地依赖于其左面和上面的所有像素。
方法是一个好方法,但是其问题在于其训练和测试的时候都需要串行地逐个生成像素,使得其速度非常慢,比如生成一个 \(N \times N\) 的图像需要进行 \(2N-1\) 次计算。并且在我看来,像素之间的关系未必有这么强烈,尽管相邻的像素之间存在很强的相关性,但是未必可以使用条件概率进行建模,从左到右生成依赖性也未必是最好的选择,大概只是一种架构上的设计。
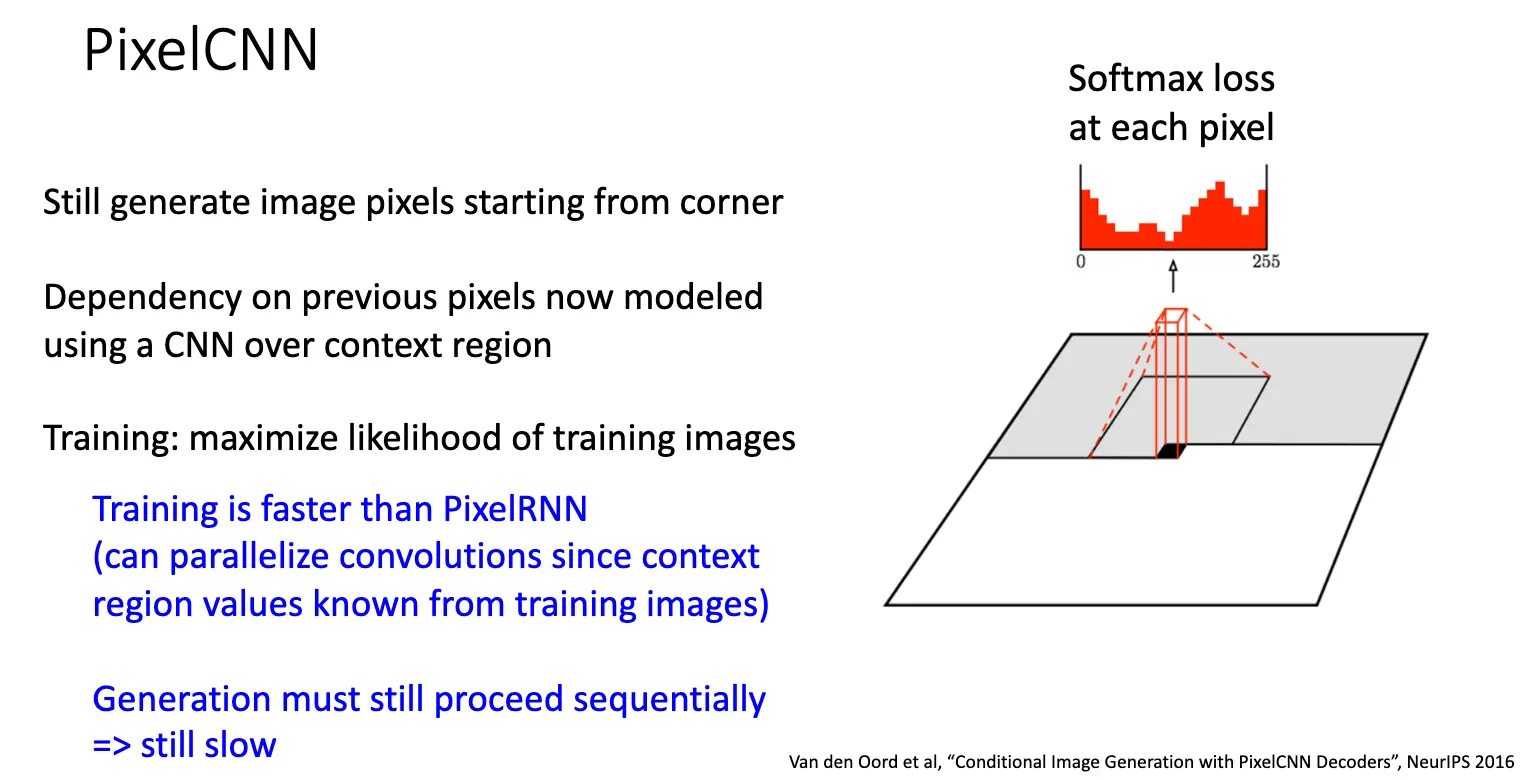
PixelCNN 是 PixelRNN 的改进版本,使用卷积神经网络/CNN 来进行建模,将像素之间的依赖通过卷积核进行建模,在训练模型的时候,我们认为每一个像素都依赖于以它为中心的卷积核覆盖的区域内的像素,这样训练就可以高度并行化,大大加快训练速度。在生成图像的时候,认为每一个像素都依赖于它左边和上边的像素,这样生成图像的时候仍然需要串行地逐个生成像素。
与自回归模型不同,变分自编码器/Variational Autoencoder/VAE 并不直接对数据的概率分布 \(p(x)\) 进行建模,其定义了一个隐式的、无法直接计算或者优化的密度函数,我们通过优化该密度函数的下界来进行间接优化。
要理解 VAE,我们首先需要理解自编码器/Autoencoder:常规的/非变分的自编码器希望从输入数据 \(x\) 中无监督地提取数据的特征向量 \(z\)/隐含表示,这样的自编码器提取的表示应该是对下游工作有意义的,比如分类、检测等任务。训练自编码器的方法也很直接——如果我们可以一起训练一个解码器,使得其可以从特征向量 \(z\) 重构出原始数据 \(x\),那么或许我们就可以认为提取出的特征是有意义的或者者说包含了数据的潜在结构。

上张图展示了一个简单的自编码器架构以及训练方式,直接使用重构出来的数据和原来的输入数据的 L2 损失作为训练目标,现在常见的架构是使用卷积神经网络/CNN 作为编码器和解码器。在训练结束之后,我们丢弃解码器,保留编码器作为特征提取器使用,将其接入下面的分类等任务或者用来初始化一个监督模型。
当然我们不希望模型全程学习到的是一个简单的恒等映射,因此我们需要对编码器提取的特征向量 \(z\) 进行瓶颈处理,比如限制 \(z\) 的维度小于 \(x\) 的维度,迫使模型学习到数据的潜在结构。
如果只从提取潜在表示的角度来看,这样的自编码器是有意义的,但是它有一个很大的缺陷:它不是概率性的模型,我们无法从中采样出新的数据点,而我们希望使用更强大的方式构建出一个带有结构的样本空间,进而可以进行插值或者采样。我们使用变分推断的方法改进这样的模型,得到变分自编码器/VAE:
在变分自编码器上,我们做的事情略有不同,我们将隐变量 \(z\) 视为一个概率分布,当要采样新的数据的时候,我们首先从隐变量的先验分布 \(p_{\theta^*}(z)\) 中采样一个 \(z\),然后将 \(z\) 输入解码器,解码器输出数据的概率分布 \(p_{\theta^*}(x \mid z)\),从这个分布中采样出新的数据点。这个先验分布 \(p_{\theta^*}(z)\) 和条件分布 \(p_{\theta^*}(x \mid z)\) 都应该比较简单,比如高斯分布(这样解码器输出的实际上就是该高维高斯分布的均值 \(\mu_{x|z}\) 和协方差 \(\Sigma_{x|z}\),另外,更多的时候我们指定这个协方差矩阵是一个对角矩阵,这样可以简化计算和存储),而隐变量的先验分布应该提前指定好——这恰符合先验分布之名,其一般是一个标准正态分布,指定了隐变量空间的结构,要求所有的有意义的隐变量都处在原点附近。解码器的参数通过训练习得。
在训练的时候,自然而然的想法就是通过最大似然估计来训练模型,如果对每一个 \(x\) 都可以观测出对应的 \(z\),那么我们就可以训练出来条件分布 \(p_\theta(x \mid z)\),这样就可以最大化
来训练参数 \(\theta\),虽然 \(p_\theta (x \mid z)\) 和 \(p(z)\) 都比较简单,但是我们无法对所有的 \(z\) 进行积分,积分完全无法进行计算,这个想法行不通。但是我们可以使用贝叶斯定理将其转化为后验概率 \(p_\theta (z \mid x)\) 的形式:
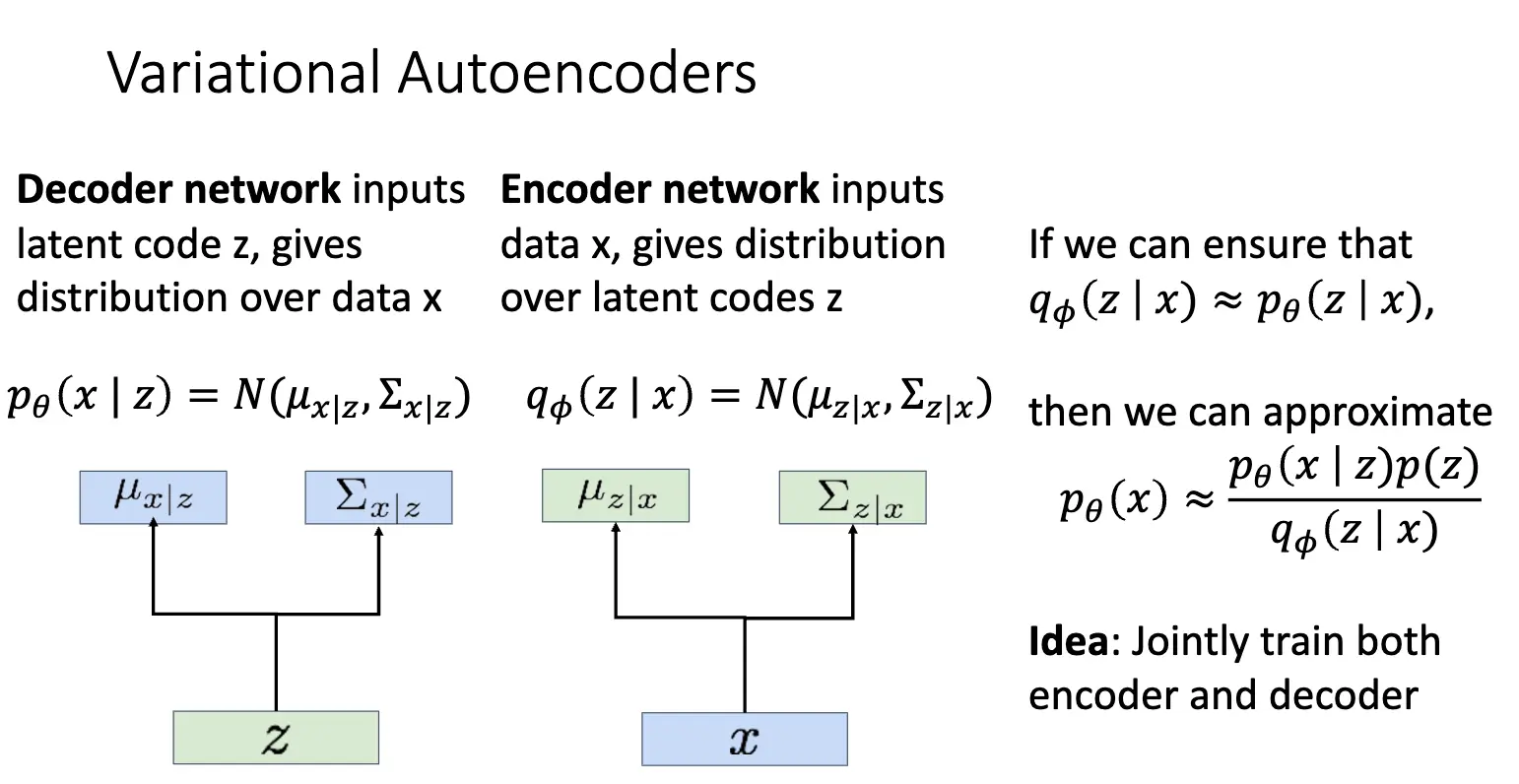
对于第一个分式,首先 \(p_\theta (x \mid z)\) 是解码器输出的条件概率,完全可以计算,先验分布 \(p(z)\) 也是已知的,因此分子部分是可以计算的,问题在于后验概率 \(p_\theta (z \mid x)\),我们无法计算出这个概率,因此我们引入一个新的神经网络 \(q_\phi (z \mid x)\) 来近似这个后验概率,这个网络称为编码器,编码器接受输入 \(x\),输出隐变量 \(z\) 的概率分布,通常也是高斯分布,其均值 \(\mu_{z|x}\) 和协方差 \(\Sigma_{z|x}\) 由编码器网络输出。这样,如果我们可以近似 \(p_\theta (z \mid x) \approx q_\phi (z \mid x)\),那么我们就可以计算出 \(p_\theta (x)\) 了。训练方式也比较直接,我们可以使用最大似然一起训练编码器和解码器。
下面我们开始对似然 \(p_\theta (x)\) 进行数学推导,推导的目标是得到一个可计算的、并且和 \(\log p_\theta (x)\) 相关的新的目标函数,这个新的目标函数称为证据下界/Evidence Lower Bound/ELBO。
注意到对一个与 \(z\) 无关的取期望不会改变其值,我们对上式两边同时取期望:
对于倒数第二行,这三项都是有意义的:第一项代表数据重构/Data Reconstruction,表示从隐变量 \(z\) 重构出数据 \(x\) 的能力;第二项是先验分布和解码器输出的隐变量分布之间的 KL 散度,表示隐变量分布和先验分布之间的差异,我们希望这个差异尽可能小,这样隐变量分布就会接近先验分布,从而可以从先验分布中采样出合理的隐变量;第三项是编码器输出的隐变量分布和解码器输出的隐变量客观的后验分布之间的 KL 散度,根本无法计算,但是 KL 散度非负,因此我们得到了一个下界,这个下界就是 ELBO,我们可以最大化 ELBO 来间接地最大化 \(\log p_\theta (x)\),进而一起训练编码器网络和解码器网络。
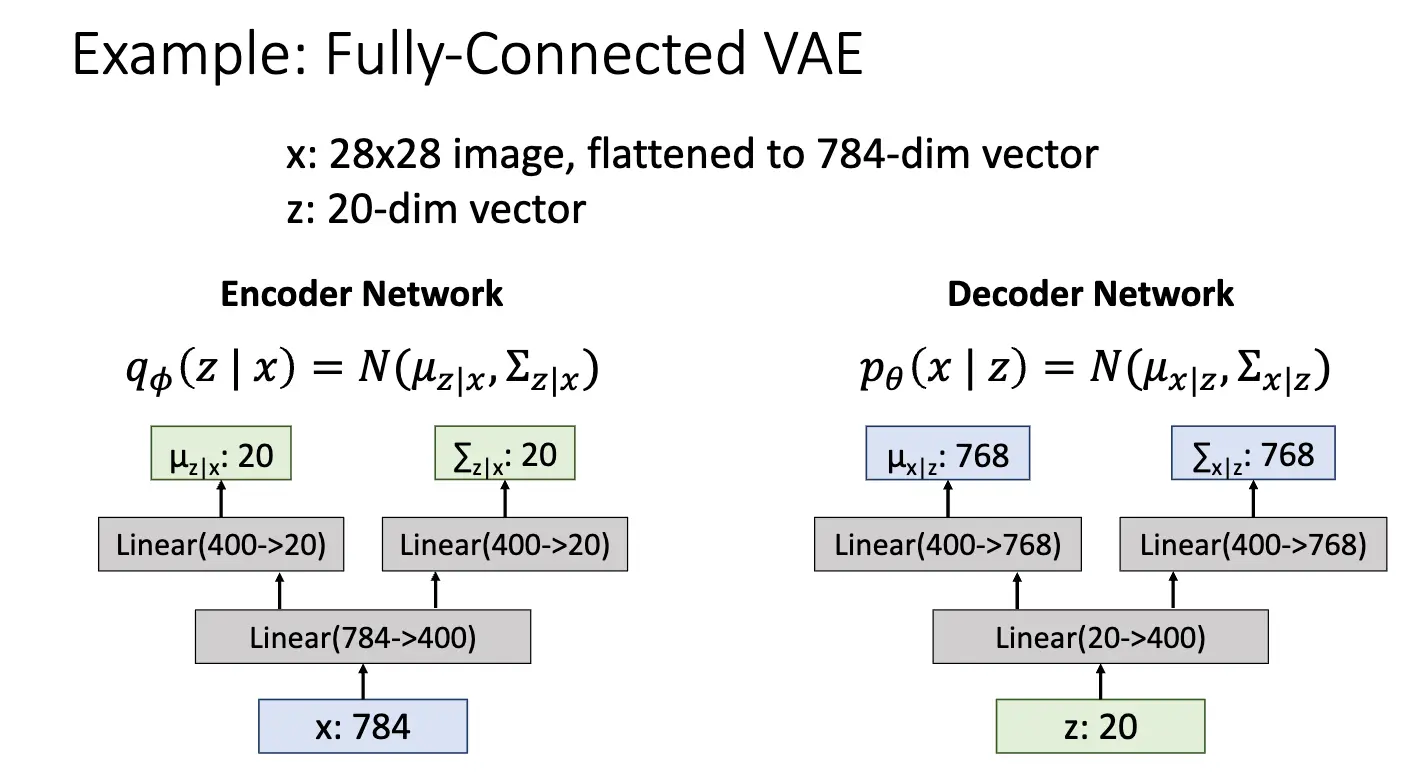
训练过程如下:我们需要知道 KL 散度部分是具有闭式解的:

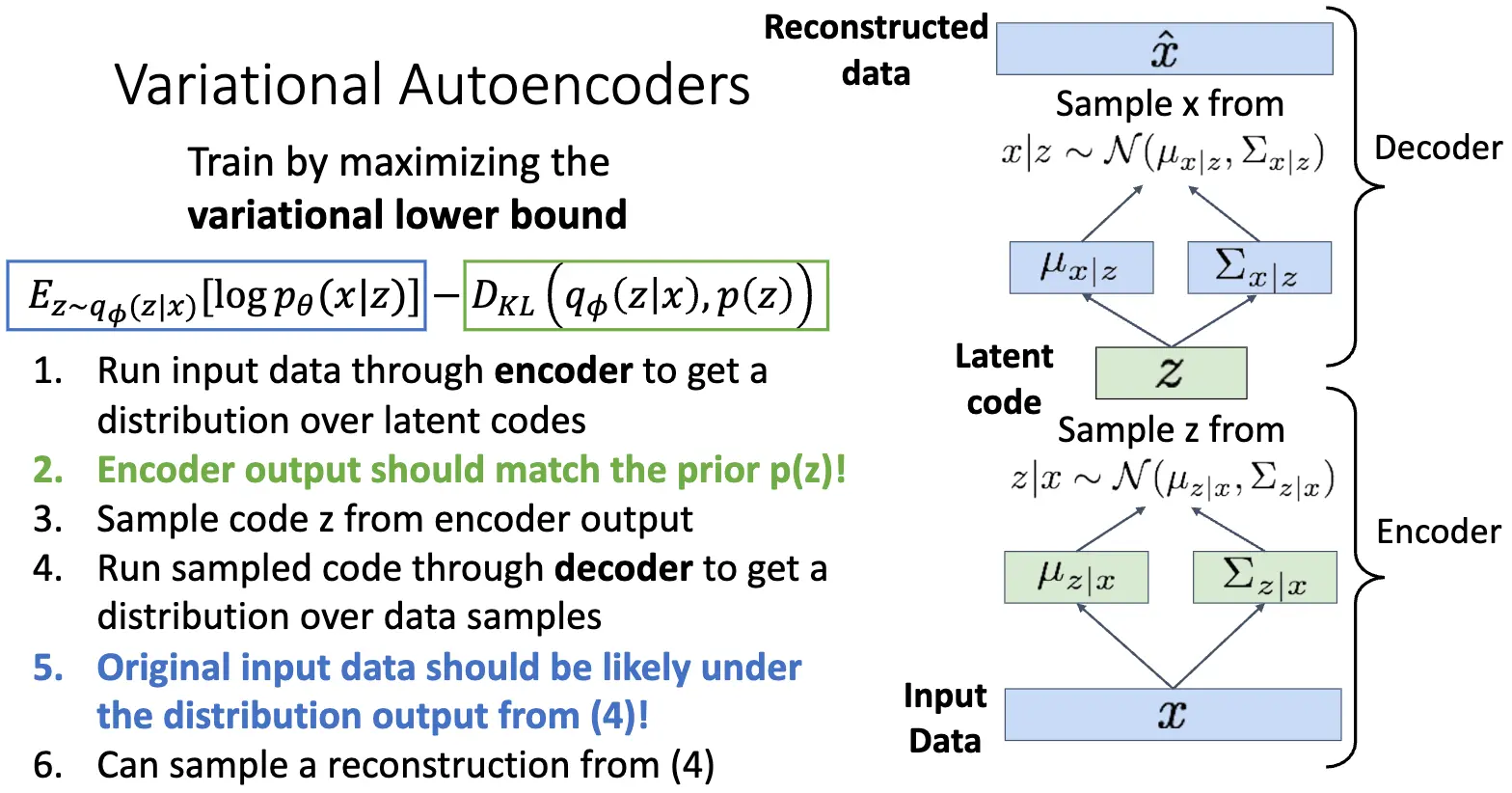
在生成新的数据的时候,我们首先从先验分布 \(p(z)\) 中采样一个隐变量 \(z\),然后将 \(z\) 输入解码器,解码器输出数据的概率分布 \(p_\theta (x \mid z)\),从这个分布中采样出新的数据点。
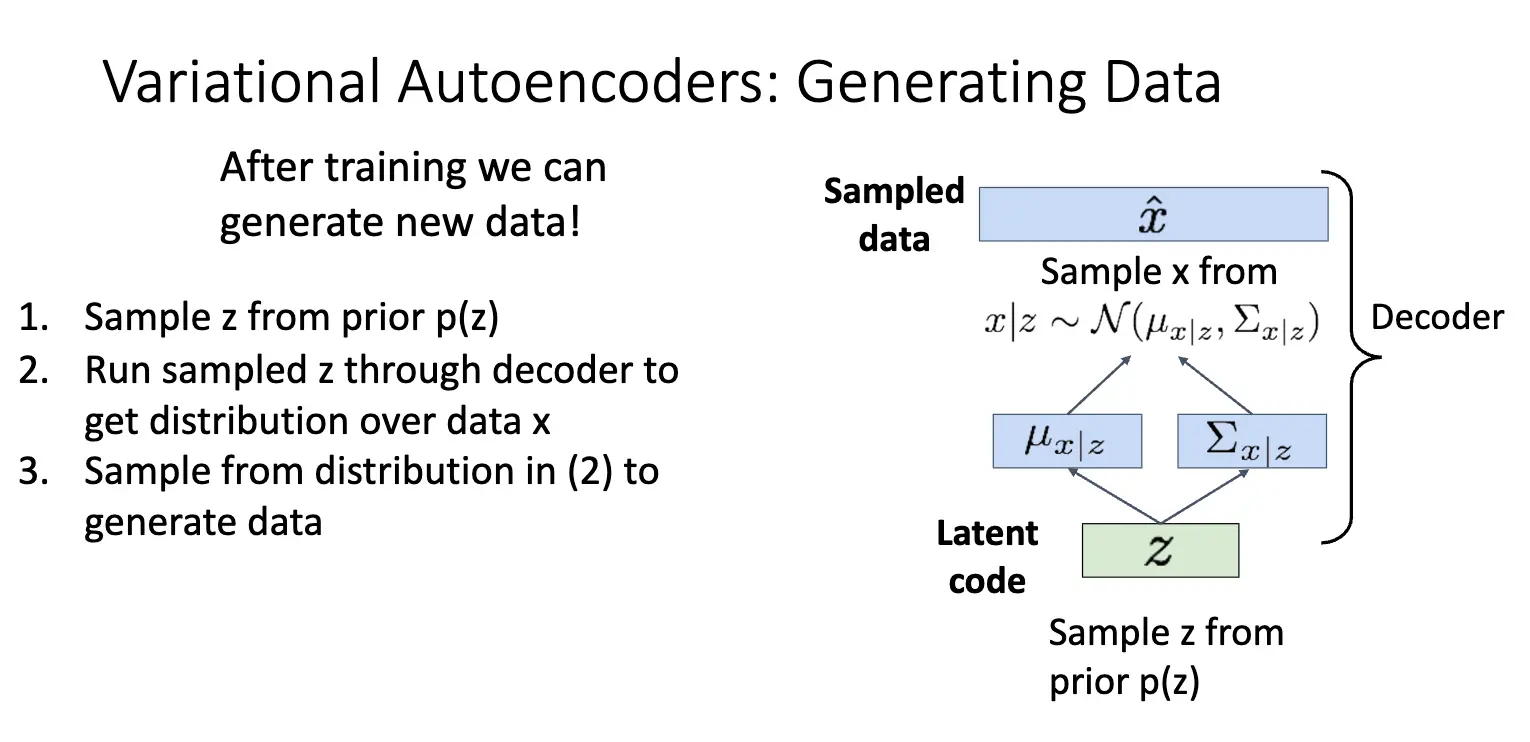
VAE 的强大也是优美之处在于其学到了一个有意义的隐空间,我们可以在隐空间进行插值等等操作:

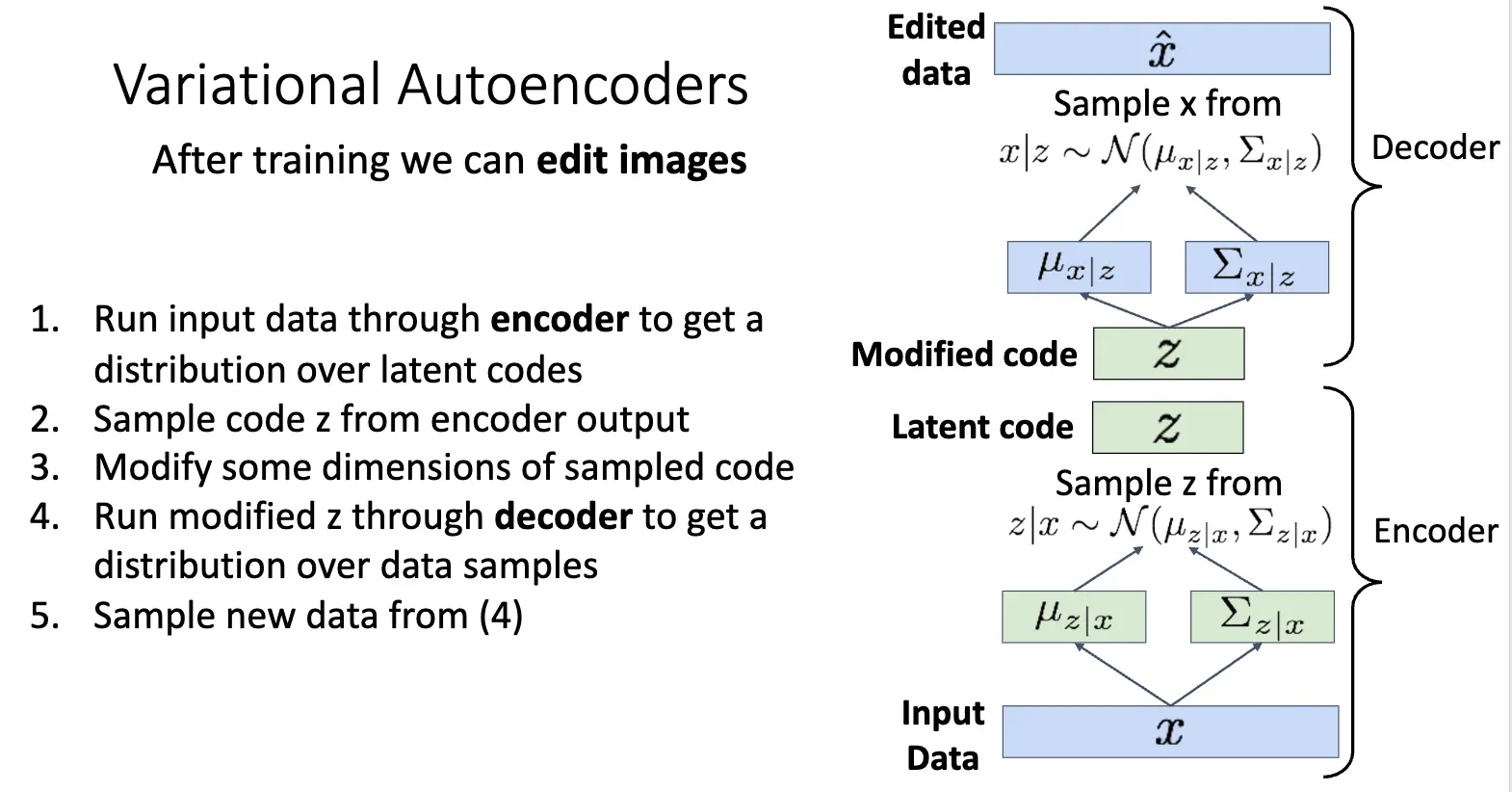

总结一下,VAE 对传统的自编码器进行了概率化的改进,使得其可以生成新的数据点,并且学到了一个有意义的隐空间,可以在隐空间进行插值和编辑操作。其优点在于:
- 提出了一个优秀的概率生成模型框架,基于概率和贝叶斯推断,数学上优美。
- 学习到了有意义的特征表示,编码器 \(q_\phi(z|x)\) 是一个强大的特征提取器。
缺点在于:
- 最大化的是下界 ELBO,而不是真正的 \(\log p(x)\),虽然是似然的下界,但是并不是类似于 PixelRNN/CNN 那样准确的估计;
- 采样和生成的图像比较模糊,尤其是纹理细节方面,和 GAN 仍有比较大的差距。
当前,变分自编码器仍然是一个活跃的研究领域,有很多改进的方向:比如使用更灵活的近似,比如不使用简单的对角高斯分布,而是使用更复杂的分布(如混合高斯 GMM、流模型)来进行改进,或者使用更加结构化的先验分布,而不是简单的标准正态分布 \(\mathcal{N}(0, I)\)。
Lecture 20: Generative Models II¶
回顾一下前面的内容,自回归模型的优势在于直接对数据分布进行建模,直接刻画像素之间的依赖关系,但是并没有一个明确的语义表示/潜变量表示,而变分模型优势在于其可以学习到一个有意义的潜变量表示,可以通过这个潜变量捕捉到数据的变化特征,进而可以控制生成。另一种方法是生成对抗网络/Generative Adversarial Networks/GANs,其放弃对数据分布进行建模,而是通过对抗的方式训练一个生成器,我们可以从中采样出新的数据点。
GAN 的设定如下:我们有从真实数据分布 \(p_{data}\) 中采样的样本 \(x_i\),希望我们可以继续从 \(p_{data}\) 中采样出新的样本。想法是引入一个潜变量 \(z\),其来自一个简单的先验分布 \(p(z)\),然后将采样的 \(z\) 输入一个生成器网络 \(G\),生成器网络输出一个样本 \(x = G(z)\),这样我们就得到了一个生成器分布 \(p_G\),我们希望这个生成器分布 \(p_G\) 尽可能接近真实数据分布 \(p_{data}\)。
训练生成器网络进而得到生成器分布的方法是引入一个判别器网络 \(D\),判别器网络是一个二分类器,接受一个样本作为输入,输出该样本来自真实数据分布 \(p_{data}\) 的概率,也就是判别样本是 Real 还是 Fake 的。我们联合训练生成器网络 \(G\) 和判别器网络 \(D\),判别器网络的目标是尽可能准确地分辨真假样本,而生成器网络的目标是尽可能愚弄判别器网络,让判别器网络认为生成的样本是真的。通过这种对抗的方式训练 \(G\) 和 \(D\),最终我们希望生成器网络可以生成出和真实数据分布无法区分的样本。
Lecture 21: Visualizing Models & Generative Images¶
Lecture 22: Self-Supervised Learning¶
Lecture 23: 3D Vision¶
在这节的内容中,我们主要考虑两类问题:一类是给出二维图像,我们需要预测其对应的三维形状,另一类是给出三维形状,我们需要给出形状的分类。这里我们假设可以访问的数据集是完全 Supervised,也就是要么有图像对应的三维形状、要么有输入的三维图像对应的标签。
RGB-D 图像也被称为 2.5D 图像,这是因为 Depth Map 实际上无法真正捕捉到被包含对象的完整结构,比如我们只知道书架的一部分被沙发挡住了,但是并不知道沙发后面的书架是什么样子的,因此我们一般认为 2.5D 图像一般比 3D 图像的表现能力稍弱,这就是其名字的来源。
当两个点云完全一样的时候,这两个点云的 Chamfer Distance 才为 0,于是我们可以选择使用 Chamfer Distance 作为损失函数来训练网络。
我希望我们的损失函数对于表示形状的方法不变的,而要求损失只取决于底层的几何形状本身。