跳转至

Part 2: Lecture 7 to Lecture 11

约 4732 个字 22 行代码 34 张图片 预计阅读时间 16 分钟

Table of Contents

Lecture 7: Convolutional Neural Networks

问题：迄今为止，我们的分类器并没有考虑图片内的空间结构信息。

解决方案：定义新的计算节点，令其在图片上直接操作，因此就有了卷积神经网络，大概有五个部分：

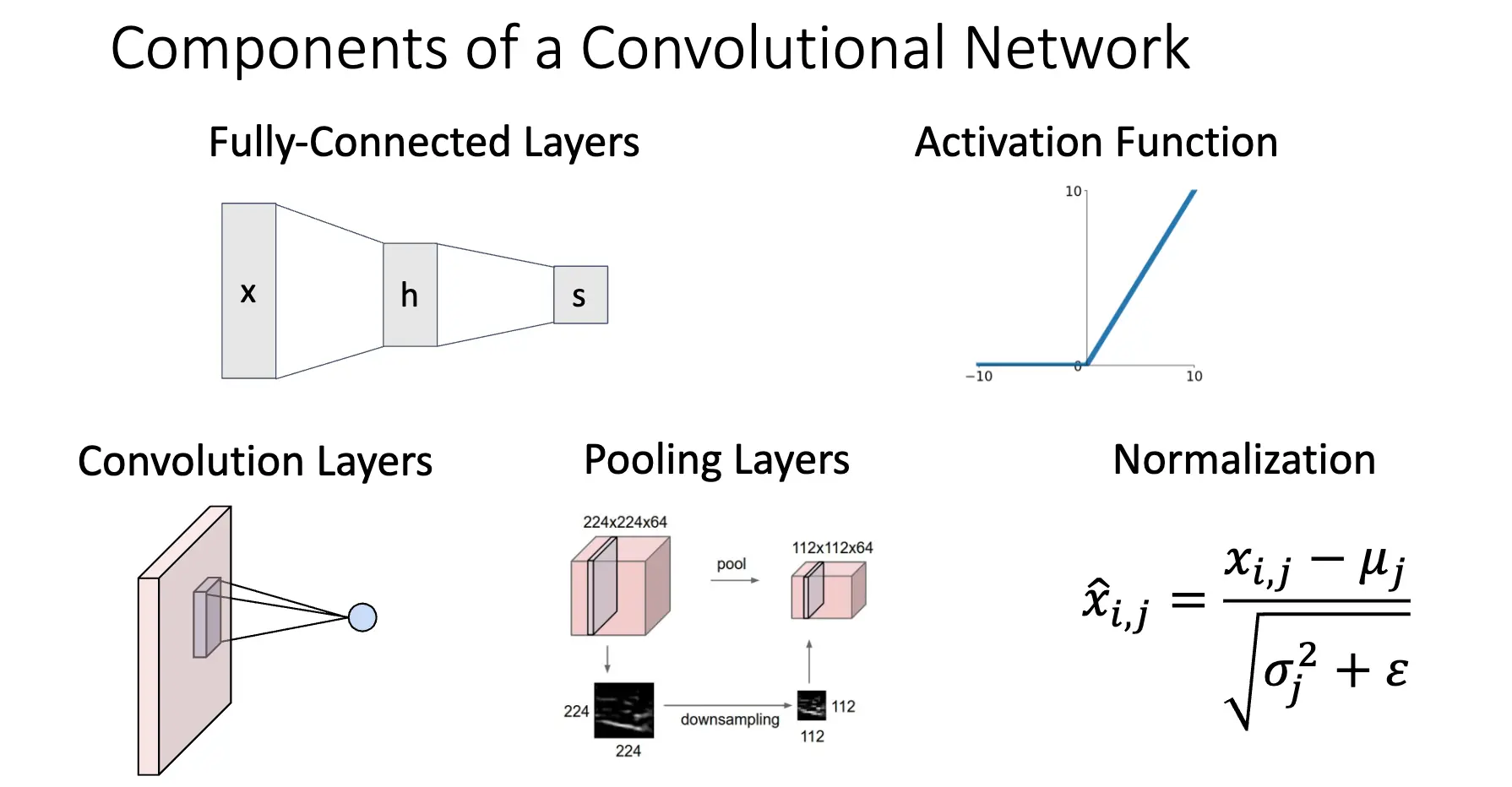
全链接网络我们已经熟悉了，对于一个 \(32\times 32\times 3\) 的图片，我们将其展平为 \(3072\times 1\) 的一个向量，然后乘以一个 \(10\times 3072\) 的矩阵，进而产生一个 \(10\times 1\) 的输出。

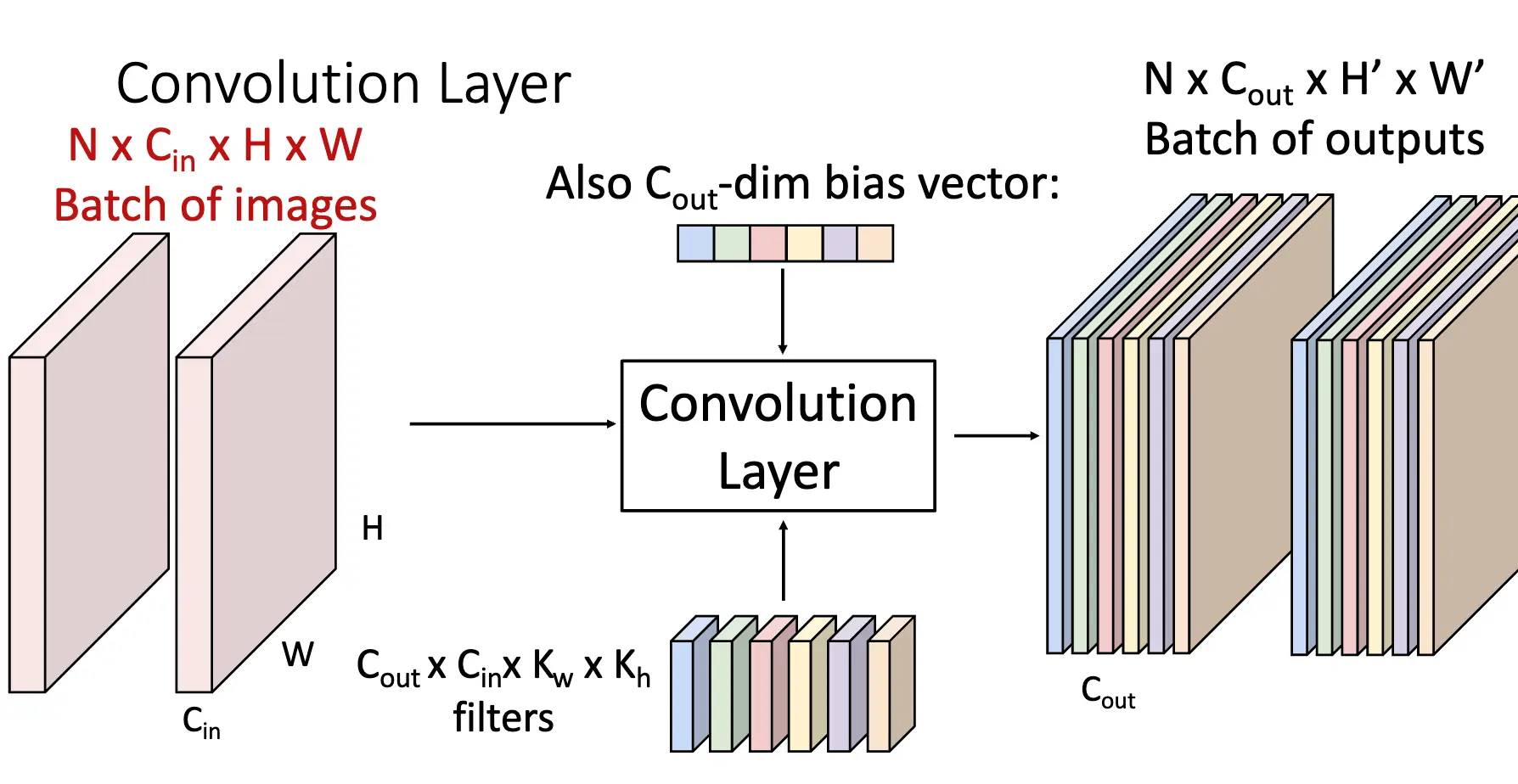
卷积层是为了处理空间结构信息的，还是对于一个 \(32\times 32\times 3\) 的图片，我们使用一个滤波器在图片上滑动并且计算点积（加上一个 bias），同时滤波器要求覆盖输入的全部深度（Filters always extend the full depth of the input volume），如果我们是用一个 \(5\times 5\times 3\) 的滤波器，滤波器在图片上滑动，最后可以得到一个 \(28\times 28\times 1\) 的输出，这个输出我们称之为激活图/Activation Map。

我们还可以考虑并行，一个是对一个图片使用多个滤波器，最后可以得到多个激活图，如果我们使用 6 个滤波器，然后我们将这些激活图堆叠起来，可以得到一个 \(28\times 28\times 6\) 的输出。同样可以考虑批处理，对于 N 张图片，我们最后可以得到 N 套堆叠起来的激活图。

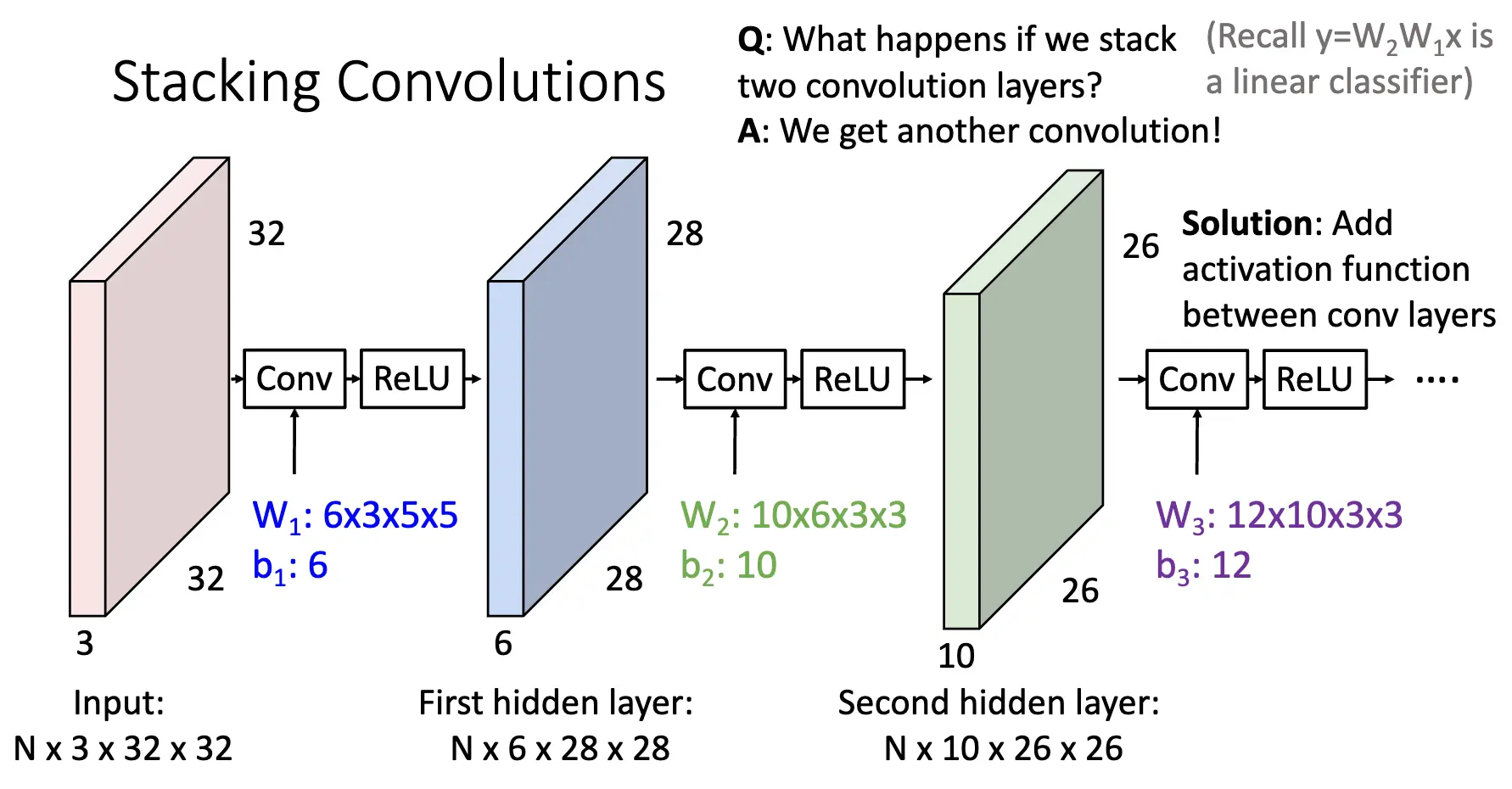
如果我们企图连续使用卷积层，那么由于卷积操作的线性性，我们最后得出的其实相当于是一个修改后的卷积层对原图片进行的卷积，和只使用一次卷积没有什么区别。因此，我们在两个卷积层之间加入一个激活函数，这样就可以引入非线性。

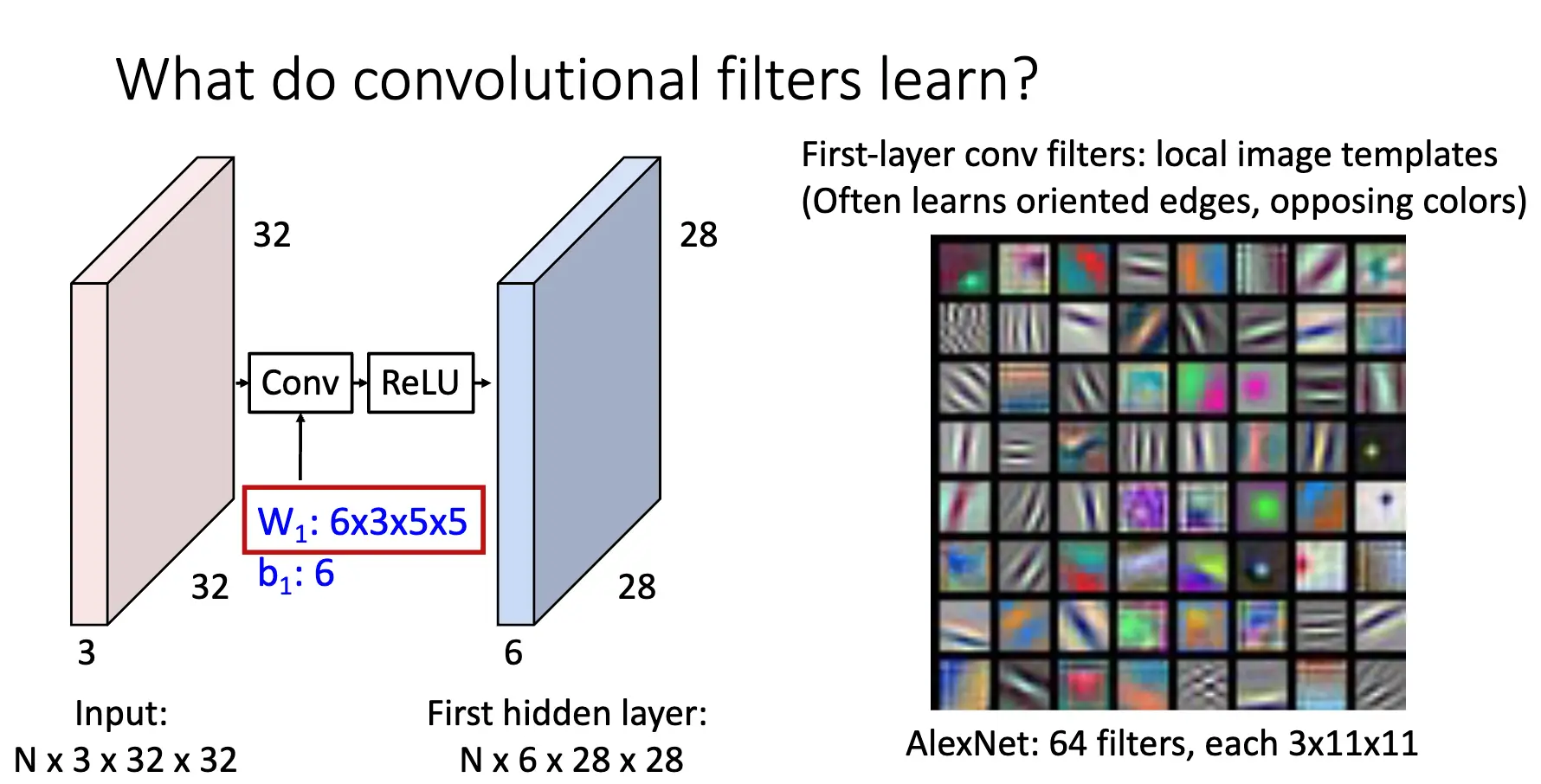
相比于之前的线性分类器和全链接网络和简单的神经网络，CNN 在第一层中实际上学习到的是局部的图片模板，经常学习的是定向的边/Oriented Edges 和相反的颜色/Opposite Colors。

卷积操作会使图片的维数发生改变，因此我们通常会使用 padding 来保持一定的图片大小。

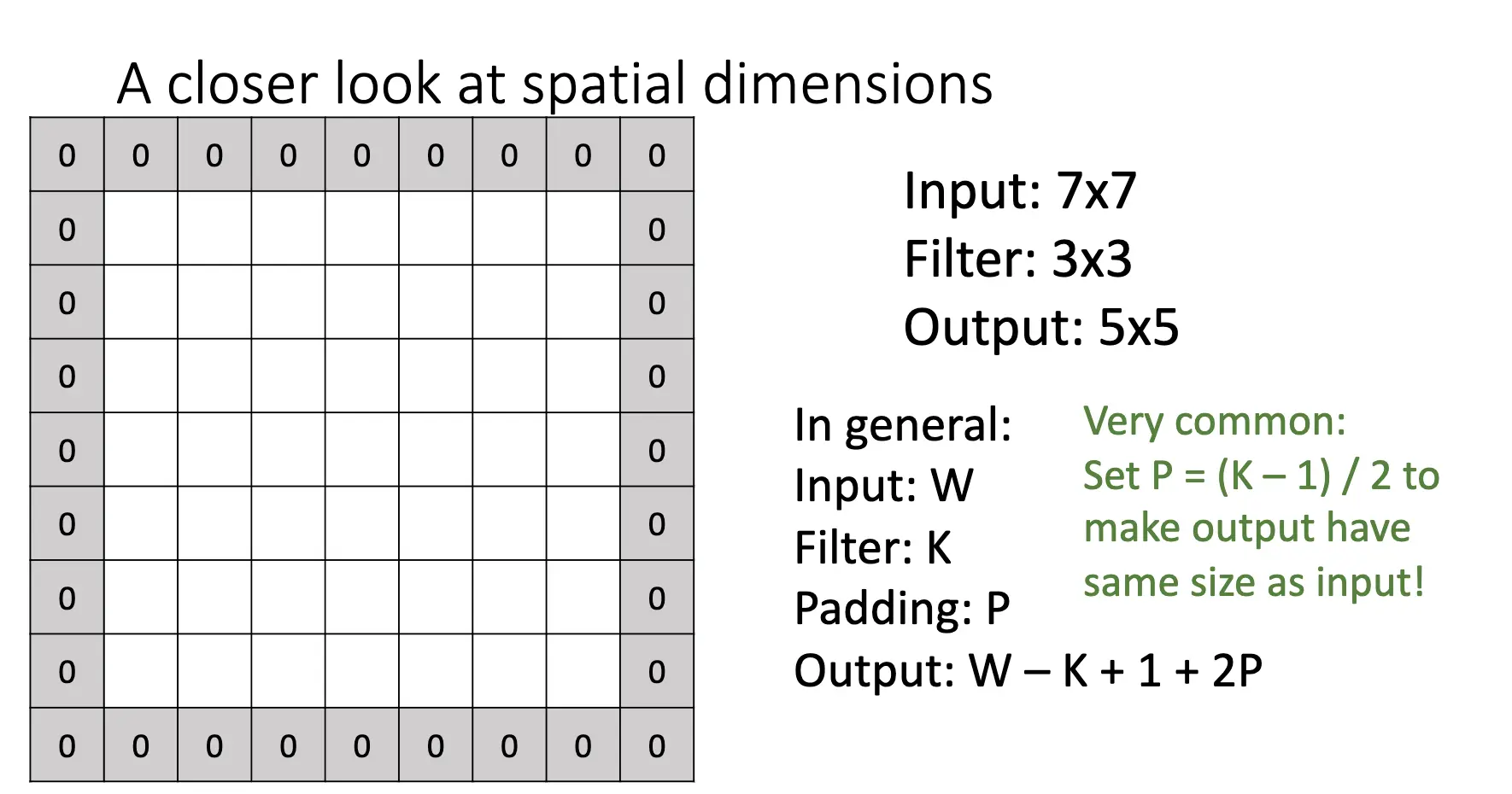
对于卷积操作，每一个激活图的元素都依赖于前一层的一个大小为 \(K\times K\) 的区域，这个区域被我们称为感受野/Receptive Field。每增加一轮卷积，感受野的大小就增加 \(K-1\)，因此，如果我们有 \(L\) 个卷积层，感受野的大小就为 \(1 + L * (K-1)\)。

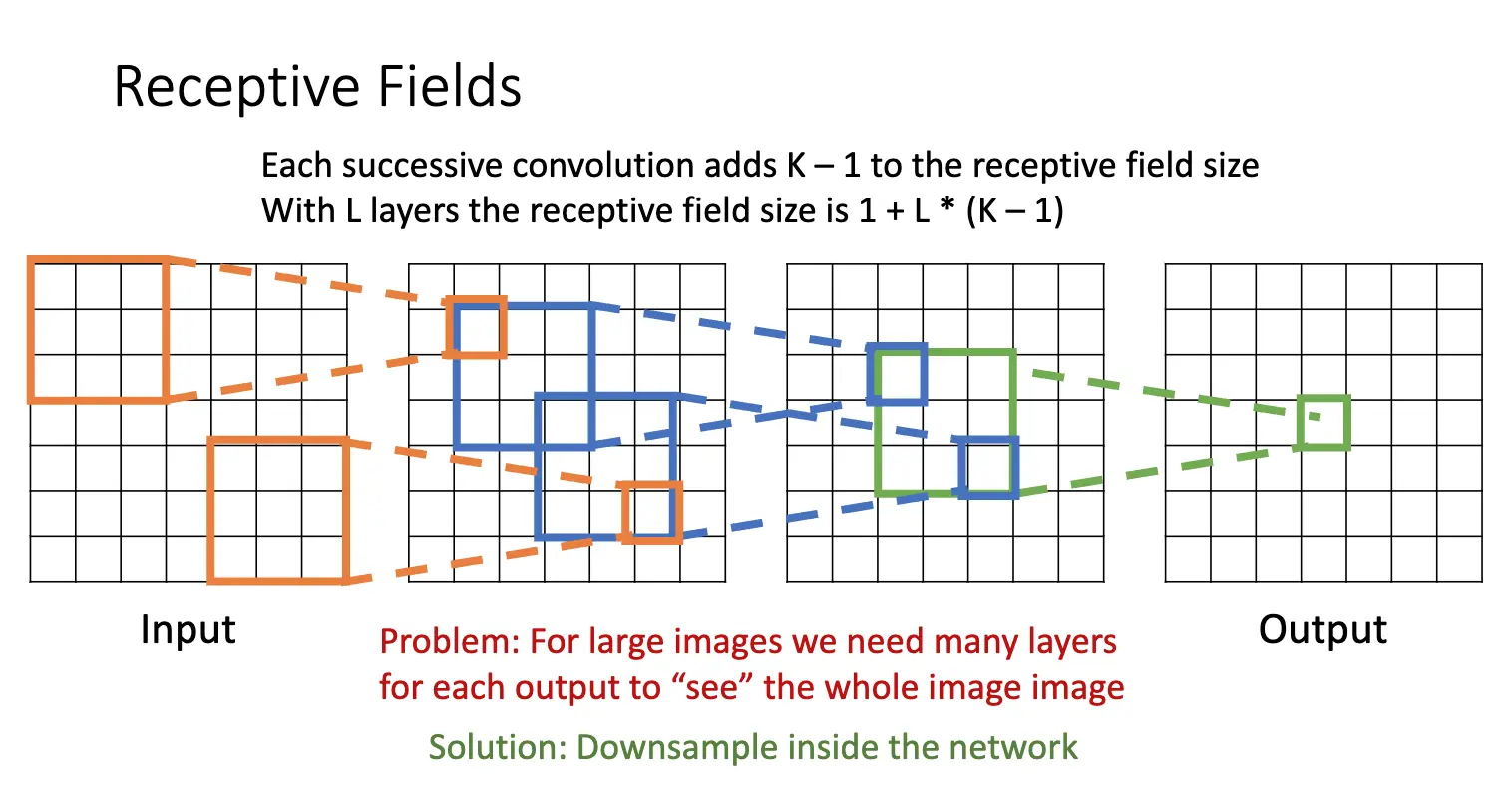
可是问题在于，对于大的图片，我们需要很多层才可以让末端的每一个神经元看到图片的全貌，这就需要下采样/Downsampling。

我们在原来的卷积操作上进行调整，原来的卷积操作是在整张图片上进行步长为 1 的滑动，我们可以引入步长卷积/Strided Convolution。

对于输入大小为 \(3 \times 32 \times 32\) 的图片，我们使用 \(10 \times 5 \times 5\) 的滤波器，步长为 1，填充为 2，输出的大小为 \(10 \times (32 + 2*2 - 5)/1 + 1 \times 32\)。进一步考虑参数，每一个滤波器我们需要学习 76 个参数，因此总共有 \(10 * 76 = 760\) 个参数，输出数目为 10240，而每一个输出背后都是 \(5 * 5 * 3\) 次乘法运算，因此总共有 \(10240 * 5 * 5 * 3 = 768000\) 次乘法运算。

一般的参数设置如下，我们很多时候抄答案就可以了：

PyTorch 为我们贴心提供了三种卷积层：

  • nn.Conv1d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')
  • nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')
  • nn.Conv3d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')

池化是另一种下采样的方式，可以看作是另一种卷积。我们使用一个二维正方形，需要考虑的是正方形的大小、池化步长和池化函数，池化操作是对正方形内框住的的元素进行池化函数操作的。常见的池化操作有最大池化/Max Pooling 和平均池化/Average Pooling。

常见的池化操作有：

经典的卷积神经网络的架构如下：[Conv, ReLU, Pool] × N → Flatten → [FC, ReLU] × N → FC。我们以 LeNet-5 为例：

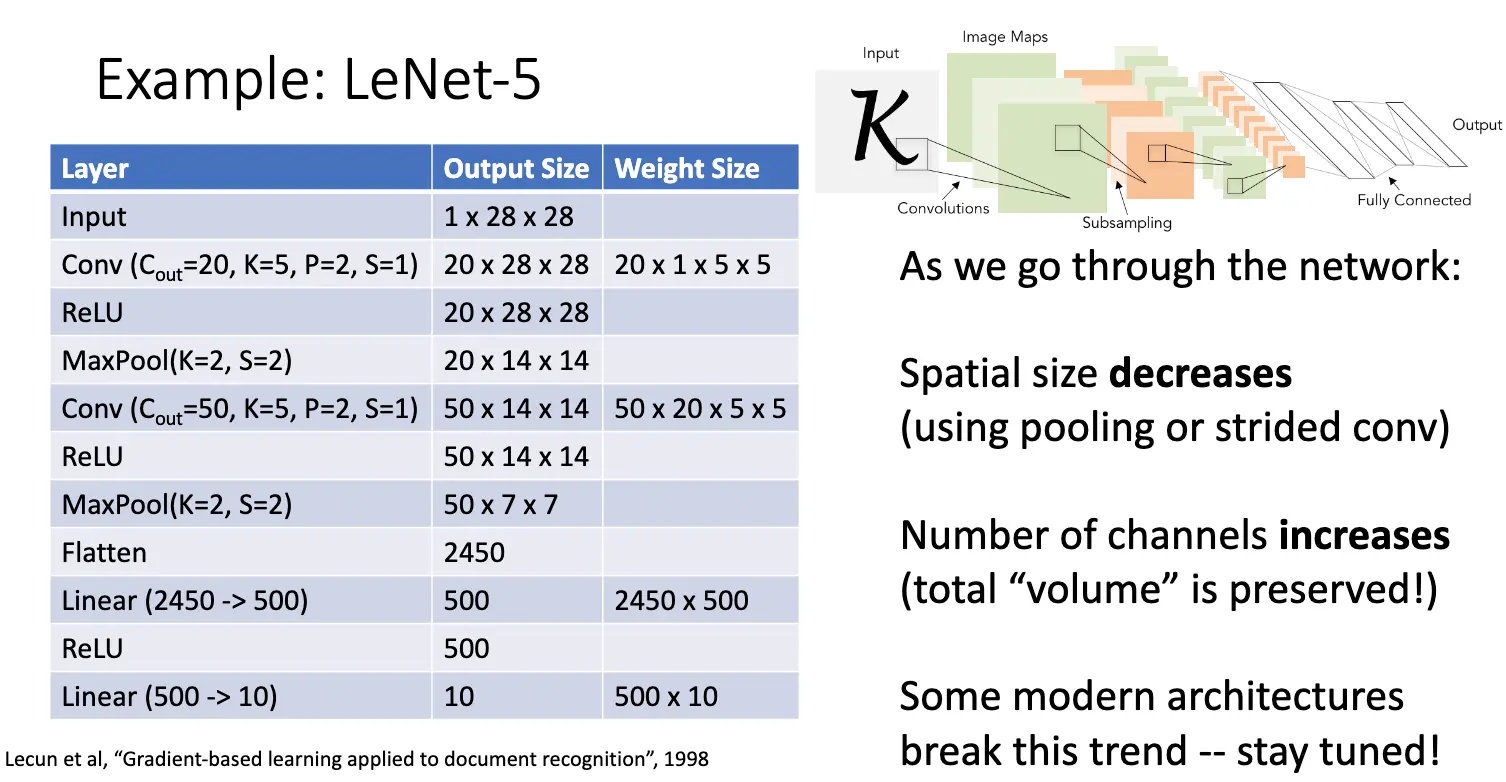
之前的很多实现有一个趋势，我们趋向于使用池化层和步长卷积使得图片的宽度变小，但是事实上又使用了多个滤波器使得通道数增加了，这样总体的体积在某种意义上保留了。现代的很多架构打破了这一点。

一个很大的问题在于，深度神经网络很难训练，我们也引入了一个叫归一化层的东西。

主要想法：我们希望减少内部协方差移位/Internal Covariate Shift（记住名词就行），进而我们要让层的输出满足零均值和单位方差。减少内部协方差移位可以提升优化速度和稳定性。

\[\hat{x} = \frac{x - \mathbb{E}[x]}{\sqrt{\mathbb{V}[x]}}\]

这是一个可微函数，因此通过计算图的想法，我们可以将其作为一个层插入我们的网络，进而反向传播可以计算梯度。

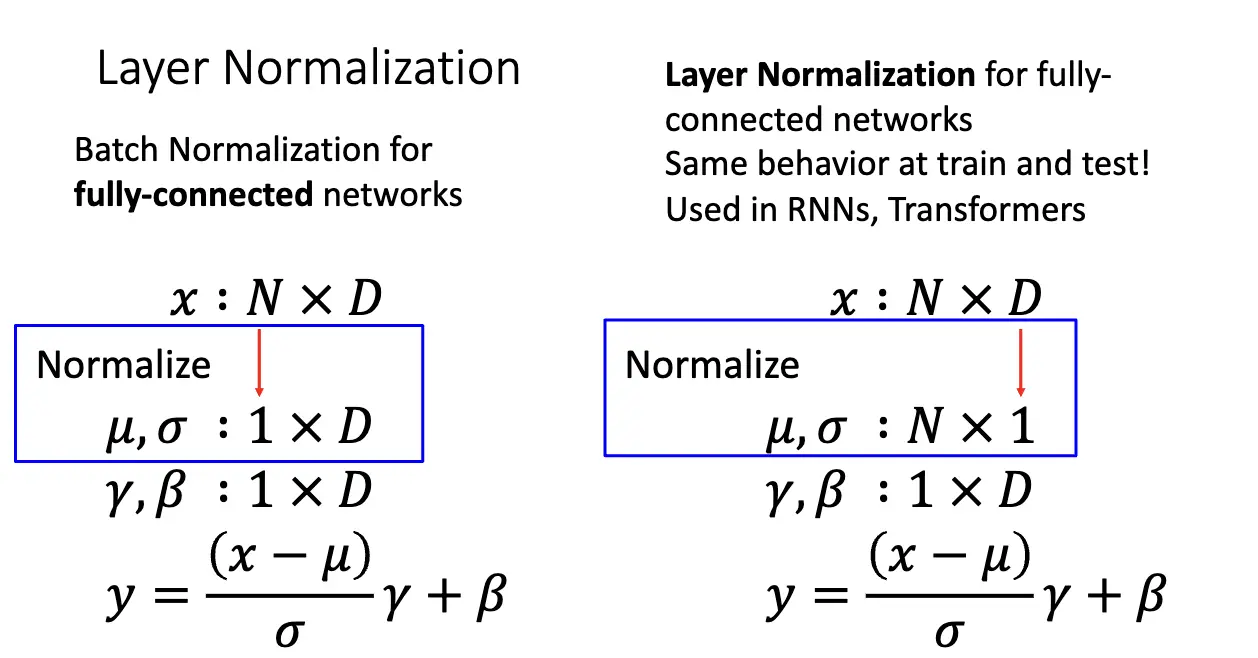
对于一个输入为 \(x \in \mathbb{R}^{N \times D}\) 的矩阵，其由 \(N\) 个长度为 \(D\) 的向量组成，我们对向量的每一个元素所在列进行归一化，或者说，我们根据每一个通道进行归一化。同样可以见得，我们在归一化项的分母上加了一个小的 \(\epsilon\) 来避免分母为零。

我们也可以引入可以学习的参数 \(\gamma\) 和 \(\beta\)，对归一化之后的变量进行缩放和平移，如果其恰好和归一化项的系数相等，那么我们就相当于进行了一次恒等变换。

但是问题来了，归一化的操作使得我们的每一个输入得到的输出都依赖于我们扔进去的别的输入，这在测试的时候是非常非常严重的问题，于是我们将测试时的均值和方差使用训练时的经验均值和方差来代替。

这样甚至还有优点，因为这时的归一化操作已经完全变成了线性操作，那么其就可以并入卷积神经网络的前面和后面的层，可以显著减少计算量。

接下来看看复杂的卷积神经网络的批量归一化：

归一化也使得神经网络变得更容易训练，允许我们使用更高的学习率，也有了和更大的收敛速率，初始化也更加鲁棒了。但是在理论层面上不太好理解，并且最大的问题还在于其在学习和训练过程中的不一致性。

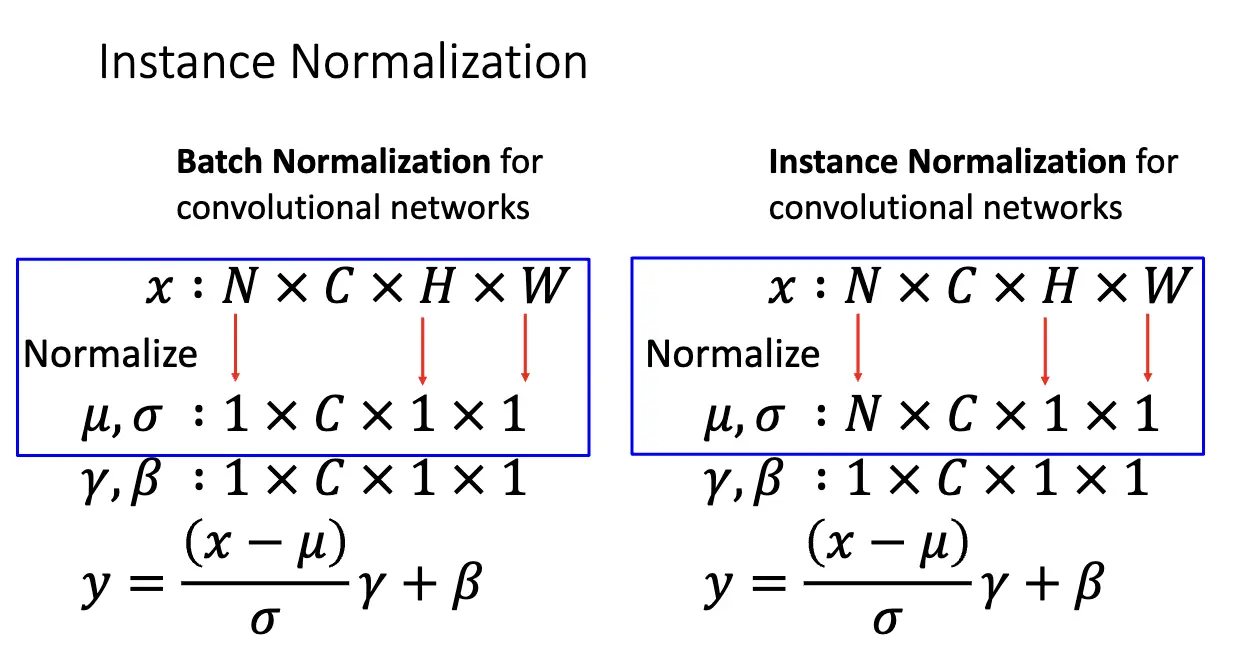
类似的还有层归一化/Layer Normalization 和 实例归一化/Instance Normalization，和批量归一化的差别在于初始化对应的通道不一样，但是本质都很相似。

Lecture 8: CNN Architectures I

2012 AlexNet：16.4% 错误率。并不深的深度卷积神经网络，两张 GTX 580 的 GPU，将模型分成两个部分，分别在一张 GPU 上训练。其架构是通过不断试错得到的，幸好效果很不错。

我们需要注意到，大多数的内存使用都发生在前几层卷积层，几乎所有的参数都集中在全链接层，大多数浮点数计算都发生在卷积层。

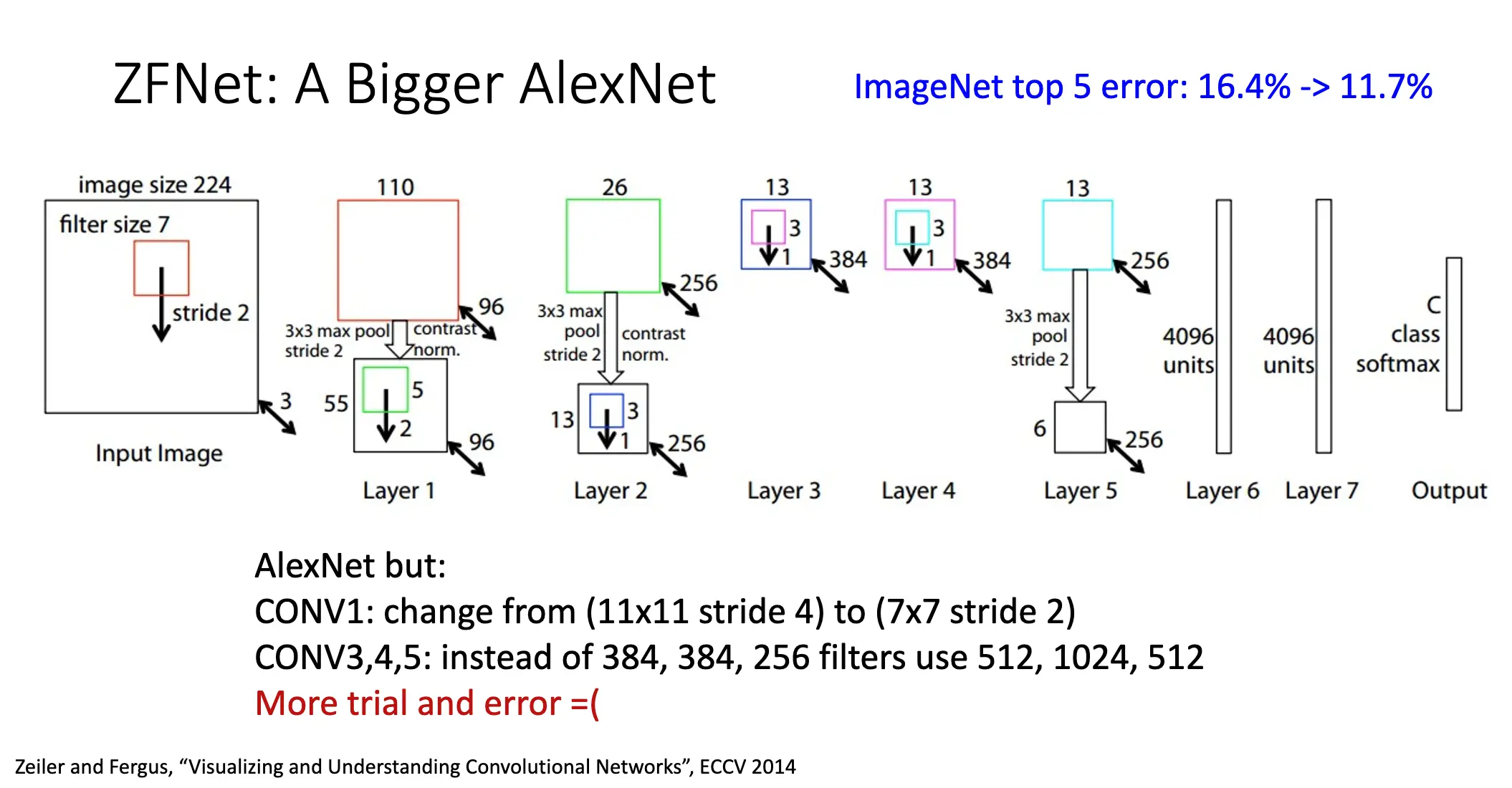
2013 ZFNet：11.7% 错误率。实际上是一个更大的 AlexNet，但是效果更好。也是试错得到的。

2014 VGG：7.3% 错误率。使用更小的滤波器，更深的网络以及更加稳定的设计。

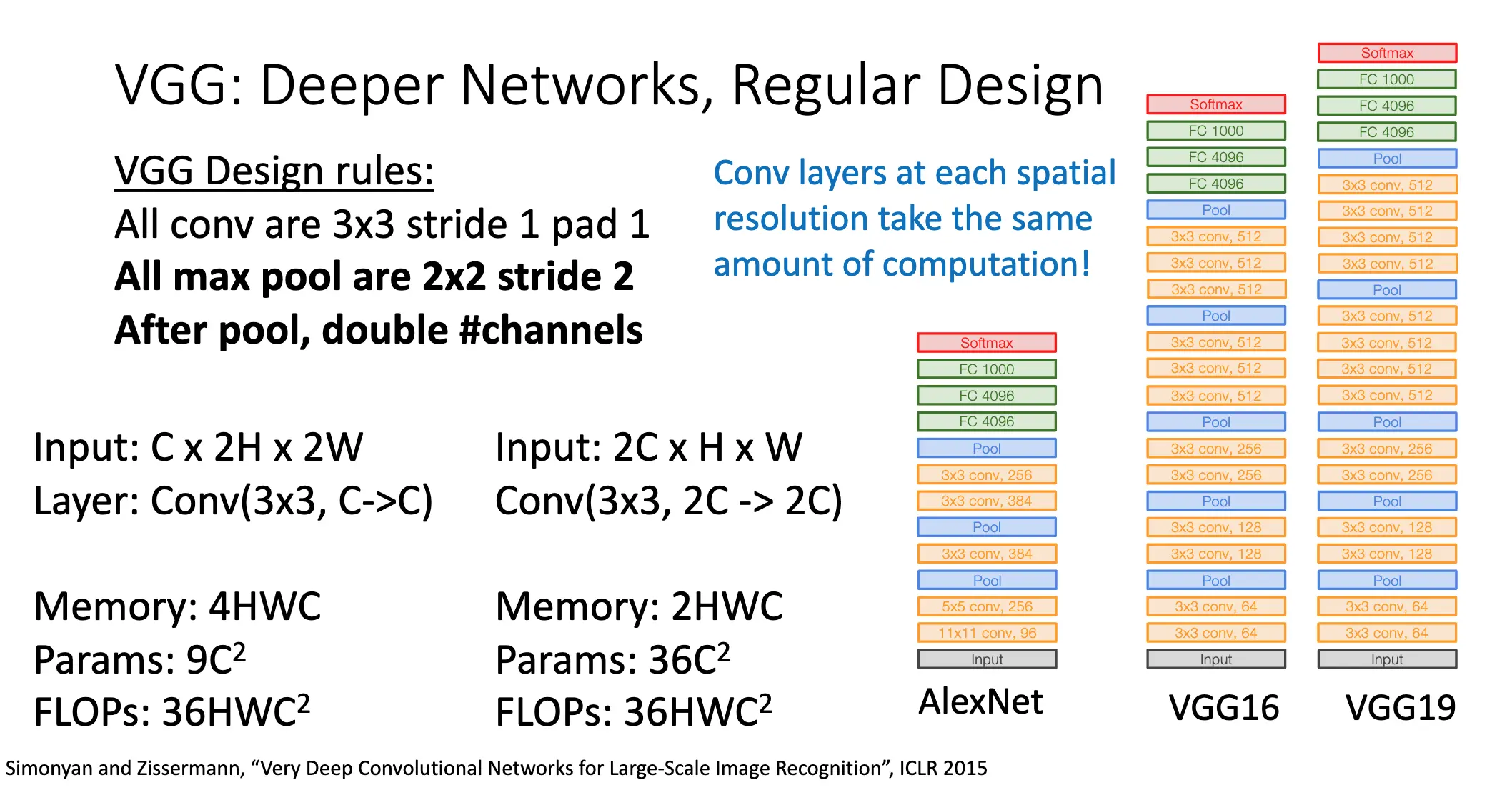
连续使用两层 \(3\times 3\) 的卷积层相比于使用一层 \(5\times 5\) 的卷积层来讲，其参数更少，浮点数计算量更少，但是就感受野的角度来看，连续使用两层 \(3\times 3\) 的卷积层和使用一层 \(5\times 5\) 的卷积层是一样的。同样，池化层将通道数加倍也可以显著减少内存使用。

2014 GoogLeNet：6.7% 错误率。更加深的网络，但是参数、内存消耗和计算量都更小了。

GoogLeNet 最开始的部分是 Stem Network：非常积极的下采样，很快从 \(3 \times 224 \times 224\) 的图片降到了 \(192 \times 28 \times 28\)。

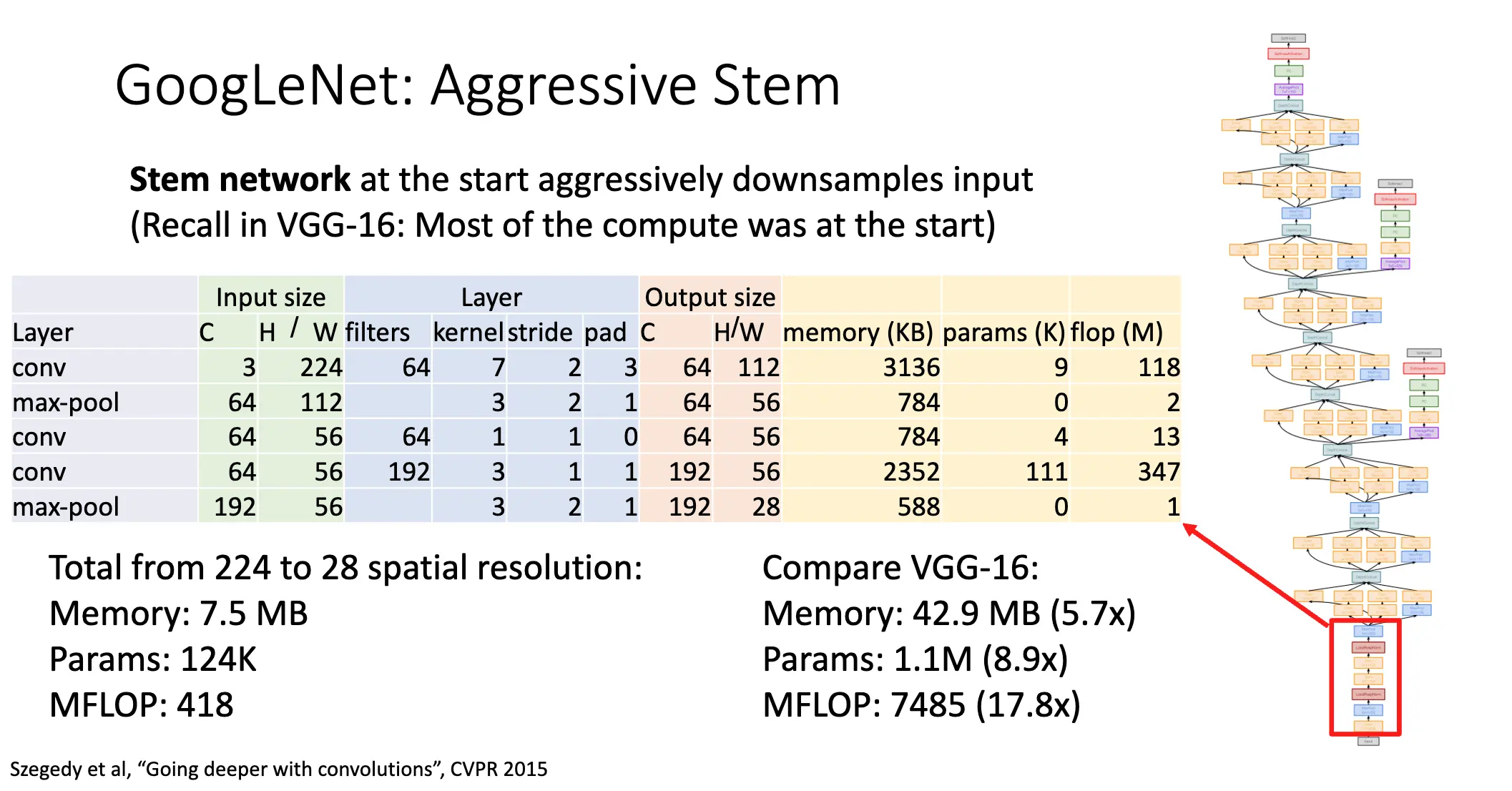
接着的是 Inception 模块，使用了分支并行，既然卷积层参数和是否使用池化是需要考虑的超参数，那么我们就进行并行，减少超参数的使用。同时也是用了 \(1\times 1\) 的卷积来减少通道数。

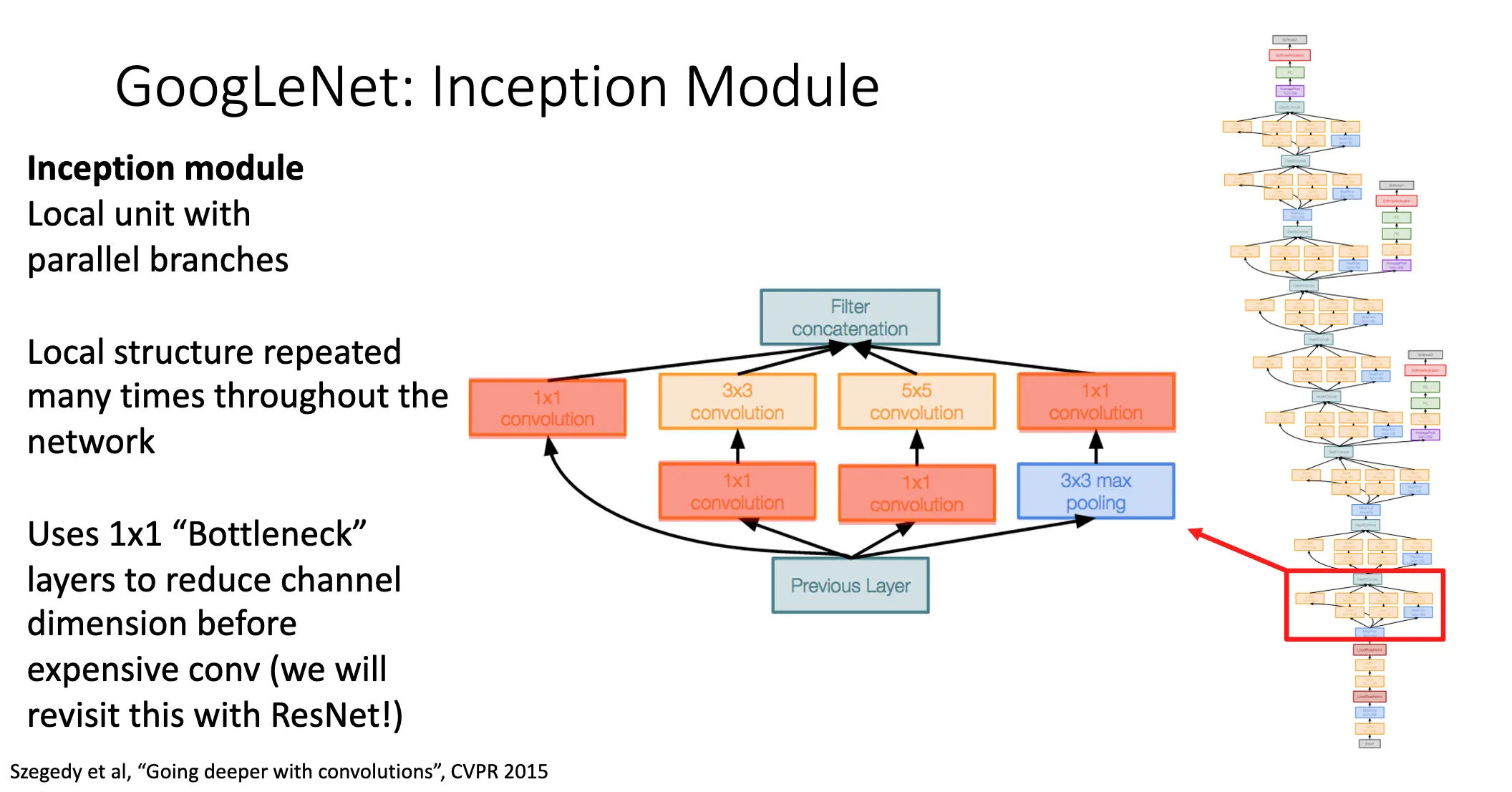
在最后，GoogLeNet 使用全局平均池化来减少空间的维数，进而令全链接层使用更少的参数，计算量也大幅降低。

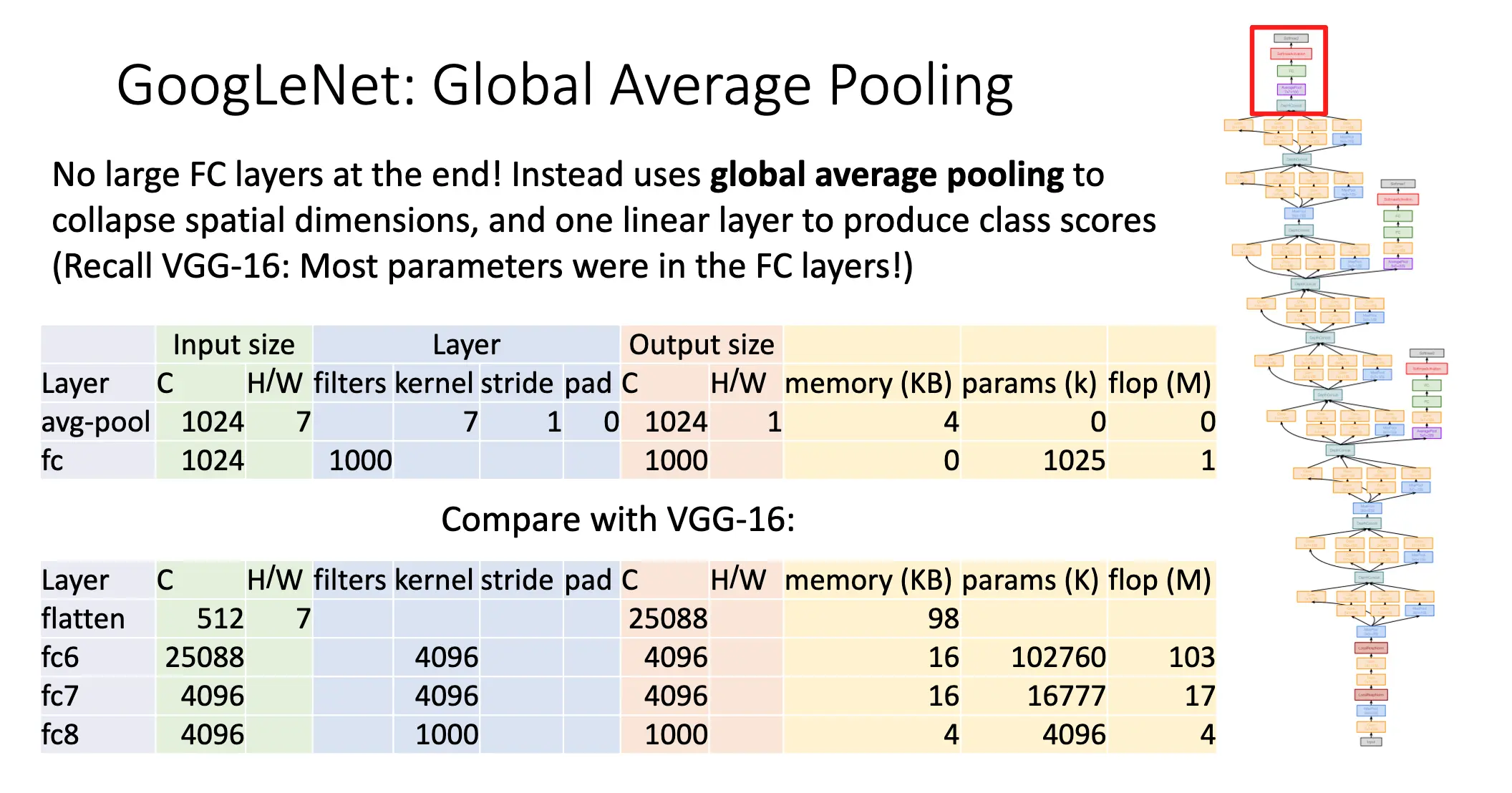
但是，直接在网络的最后训练的效果并不是很好，网络过于深了，梯度消失的问题很严重。GoogLeNet 使用辅助分类器/Auxiliary Classifiers 来缓解这个问题。在网络的中间层加入了几个辅助分类器。有了批归一化之后就不再需要辅助分类器了。

2015 ResNet：3.6% 错误率，152 层。动机：批归一化可以使得我们很容易训练超过十层的神经网络，但是一旦过深，就很难训练了。深层神经网络和浅层神经网络对比而言，测试误差会更大，最初的猜想是过深的神经网络会导致过拟合，但是实际上训练误差也很大，因此深层神经网络其实是欠拟合。

理论上深层神经网络完全可以模拟浅层神经网络，只需要从浅层神经网络中复制对应的层，然后令额外的层学习恒等映射就好了。我们猜想问题其实来自于优化，于是我们改变网络结构使得学习恒等映射变得容易。

Kaiming He 等人提出了残差网络/Residual Network，给出的解答非常简单，在一些层之间加入一个加性的 Shortcut Connection，如果我们将中间层设为 \(F(x)\)，那么加入了 Shortcut Connection 之后，我们就有 \(F(x) + x\) 去拟合 \(H(x)\)。

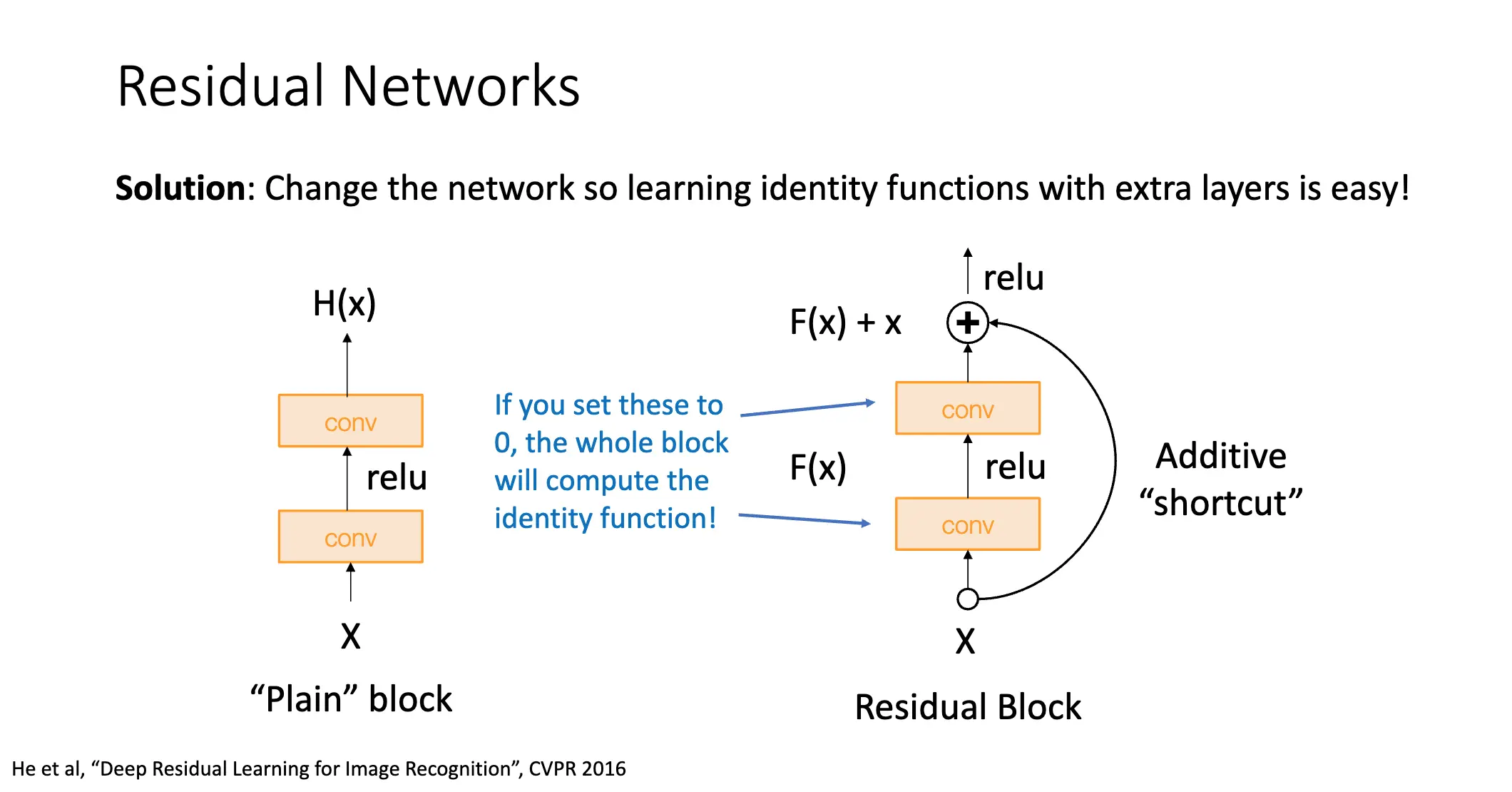
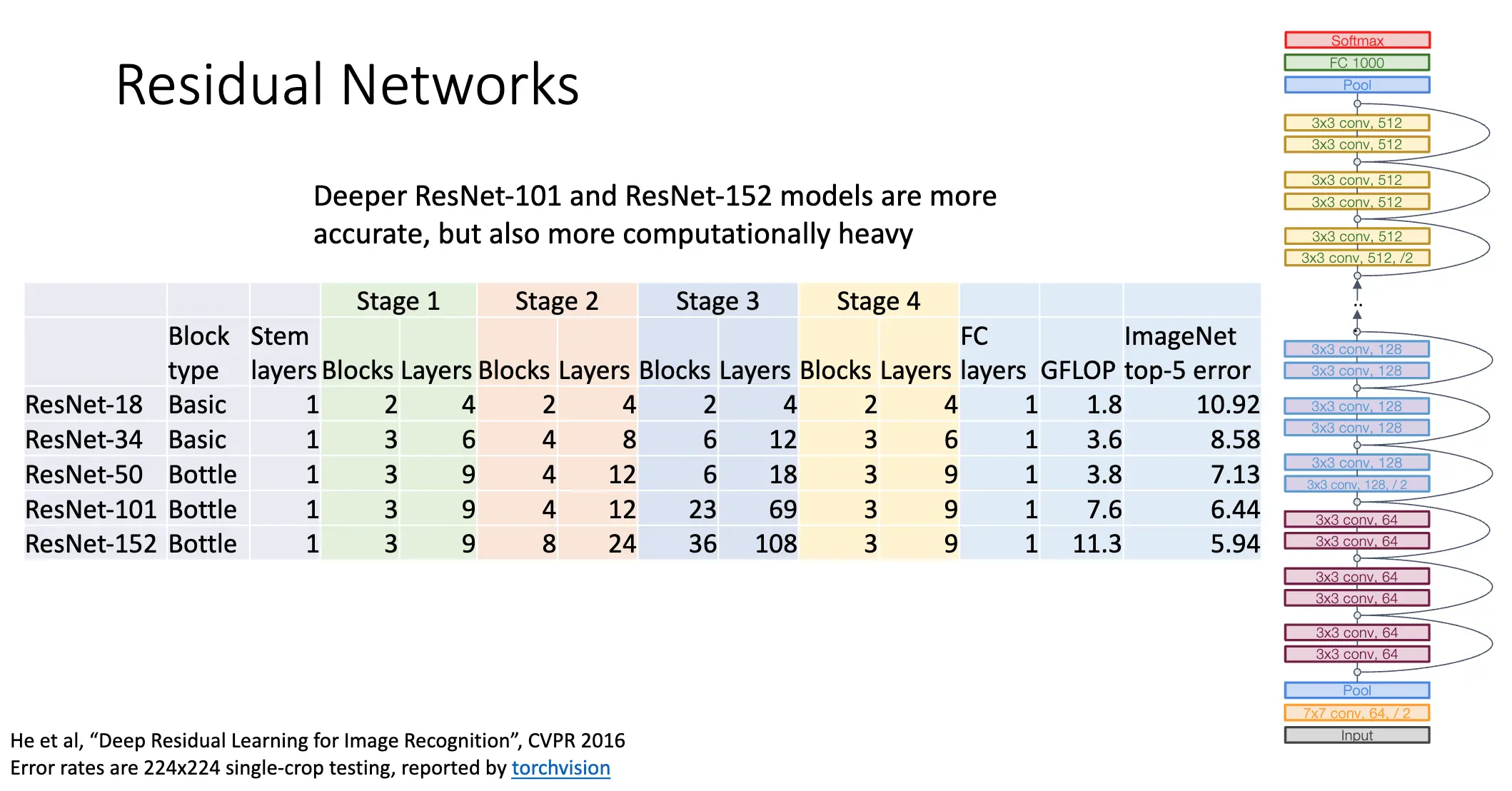
除此之外，ResNet 还学习了很多 GoogLeNet 和 VGG 的特性，比如在最开始的阶段积极下采样，在最后使用全局平均池化。我们也可以见得，ResNet 将整个网络分为不同的阶段，每一个阶段的第一个卷积层使用步长为 2 的卷积来折半分辨率，并且加倍通道数。

总体而言 ResNet 的的深度更深了，但是其需要的计算量大大降低。

另外，\(1\times 1\) 的卷积层可以在降低计算量的时候，增加层数和非线性。这样的层我们称之为瓶颈层/Bottleneck Layer。

瓶颈层可以显著提升神经网络的深度，并且降低误差。

后续还有别的更新的网络，在第 11 讲中会介绍。

Lecture 9: Training Neural Networks I

激活函数：激活函数 \(f\) 对输入 \(\sum_{i} w_i x_i + b\) 进行非线性变换，我们常见的激活函数有：

  • Sigmoid：\(f(x) = 1/(1 + e^{-x})\)
  • Tanh：\(f(x) = (e^x - e^{-x})/(e^x + e^{-x})\)
  • ReLU：\(f(x) = \max(0, x)\)
  • Leaky ReLU：\(f(x) = \max(0.01x, x)\)
  • ELU：\(f(x) = \begin{cases} x, & x \geq 0 \\ \alpha (e^x - 1), & x < 0 \end{cases}\)
  • GELU：\(f(x) = x \sigma(1.702x)\)

先从 Sigmoid 函数谈起，Sigmoid 在深度学习发展初期很受欢迎，主要是其和概率良好的对应关系和对神经元的很好的描述，但是后来发现其存在的很严重的问题，它就和 tanh 一样，很少被使用了。

  1. Saturated neurons kill the gradient：也就是梯度消失问题，这是最严重的。当输入很大或者很小的时候，梯度会变得很小，根据链式法则，这就会导致其下游的神经元梯度很小，进而导致梯度消失。
  2. Sigmoid outputs are not zero-centered：也就是输出不是零均值的，考虑 \(h_i^{(\ell)} = \sum_j w_{i,j}^{(\ell)} \sigma \left( h_j^{(\ell-1)} \right) + b_i^{(\ell)}\)，其中 \(h_i^{(\ell)}\) 是第 \(\ell\) 层的第 \(i\) 神经元，等下两个参数是权重和偏置。求微分可以发现：\(\dfrac{\partial L}{\partial w_{i,j}^{(\ell)}} = \dfrac{\partial L}{\partial h_i^{(\ell)}} \cdot \sigma \left( h_j^{(\ell-1)} \right)\)，这样就可以看出来，所有 \(w^{\ell}_{i,j}\) 的梯度都和 \(\dfrac{\partial L}{\partial h_i^{(\ell)}}\) 的符号相同，在二元条件下就会产生丑陋的锯齿状。最大的问题是这样的同向梯度其实限制了梯度的方向，使得梯度下降的效率降低，这在高维的时候尤其严重。但是实践中并没有那么严重，批归一化就可以缓解这个问题。
  3. \(\exp\) is a little expensive：\(\exp\) 的计算量比较大。

Tanh 也一样，虽然解决了零均值的问题，但是梯度消失的问题依然存在。

ReLU 性质非常不错，在 \(x > 0\) 的时候，梯度为 1，解决了一部分的梯度消失，正区间内不会饱和。计算也容易，收敛也迅速。虽然不是零均值的，并且在 \(x < 0\) 的时候，梯度为 0。梯度为 0 的问题非常烦人，这导致很多神经元干脆不会更新，因此很多时候我们将 ReLU 神经元使用一个很小的正偏置来初始化，比如使用 0.01 初始化。

好一点的是 Leaky ReLU，其实 Leaky ReLU 接收一个超参数 \(\alpha\)，定义为 \(f(x) = \max(\alpha x, x)\)。这就解决了梯度消失的问题，我们也可以使用 PReLU/Parametric ReLU 来通过反向传播学习 \(\alpha\)。

另一个是 Exponential Linear Unit/ELU，定义为 \(\operatorname*{ELU}(x) = \begin{cases} x, & x \geq 0 \\ \alpha (e^x - 1), & x < 0 \end{cases}\)，其中 \(\alpha\) 是一个超参数，默认为 1。其保留了 ReLU 的所有优势，输出均值也更接近于 0。其在负值区域有饱和线性，可以抑制异常值的影响，具有更好的噪声鲁棒性。

更牛逼的是 Scaled Exponential Linear Unit/SELU，定义为 \(\operatorname*{SELU}(x) = \lambda \operatorname*{ELU}(x)\)，其中 \(\lambda\) 和 \(\alpha\) 是根据经验设置的常数，\(\lambda = 1.0507\) 和 \(\alpha = 1.6732\)，理解这个常数需要阅读一篇九十多页的论文。这个函数对于深度神经网络效果会更好，并且具有自归一化的性质，可以不使用批归一化训练深度神经网络。

最后是 Gaussian Error Linear Unit/GELU，定义为 \(\operatorname*{GELU}(x) = x \mathbb{P}(X \leq x)\)，其中 \(X\) 服从标准正态分布，可以近似计算为 \(\operatorname*{GELU}(x) \approx x\sigma(1.702x)\)。主要思想是对输入随机乘以一个伯努利分布，大的值更加容易乘以 1，小的值更加容易乘以 0，然后对随机性取期望。这在 Transformer 中效果很好，非常常见。

对激活函数的建议大体如下：

数据预处理：只需要考虑上面 Sigmoid 提到的第二个问题，就可以知道为什么我们希望使用零均值的输入。常见手法/处理后的数据类型有这些：

  • 零均值数据：X -= np.mean(X, axis=0)；
  • 标准化数据：X /= np.std(X, axis=0)；
  • 去相关数据：使用主成分分析，通过协方差矩阵调整数据云的分布，使得特征之间是不相关的；
  • 白化数据：去相关数据 + 标准化数据。

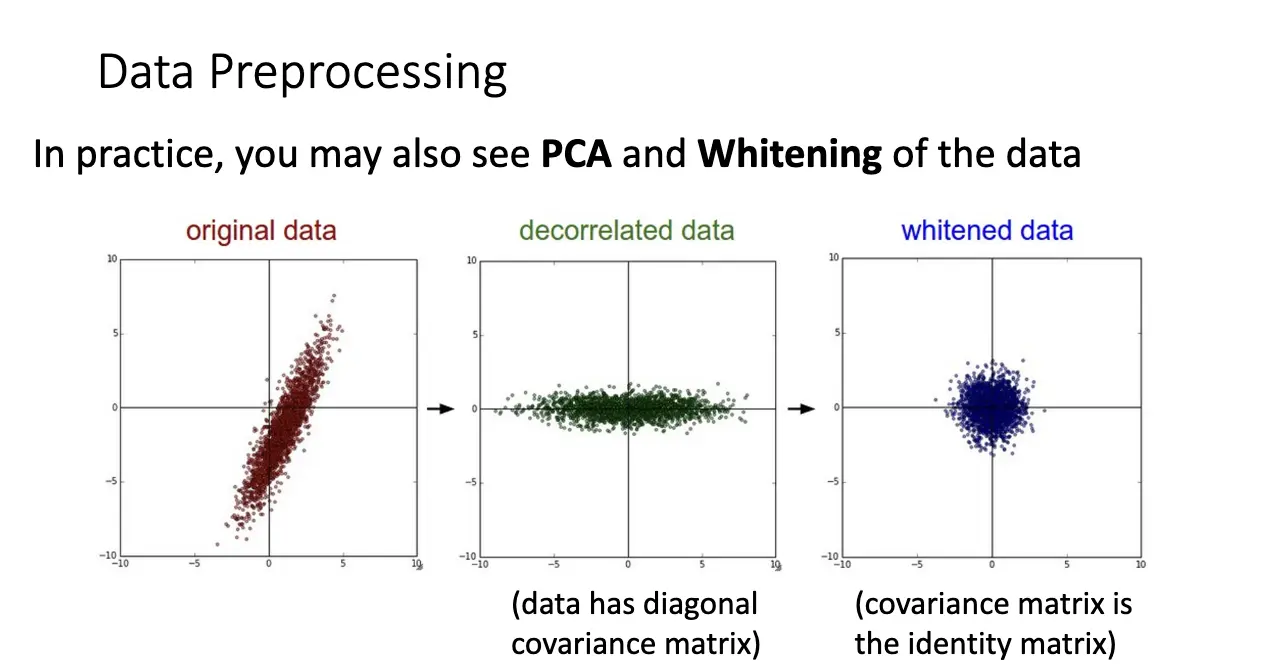
PCA 和白化数据相比而言不太常见。

预处理后的标准化数据对权重的微小改变更加不敏感了，令我们更加容易去进行优化。

权重初始化：

如果我们使用 Tanh 进行激活：

  • 全是 0/某一个常数：输出当然全是 0，所有的梯度都是一样的，因此我们没有打破对称性；
  • 使用小的随机数进行初始化：W = 0.01 * np.random.randn(Din, Dout)，还不错，但是这对小的神经网络很实用，但是对于大的神经网络就会出现一些问题：在多次训练之后，神经元会在 0 附近饱和，导致梯度消失；
  • 使用大的随机数进行初始化：W = 0.05 * np.random.randn(Din, Dout)，这会使神经元在 -1 和 1 两个值的附近饱和，也会导致局部梯度为 0，导致梯度消失；
  • Xavier 初始化：W = np.random.randn(Din, Dout) / np.sqrt(Din)，非常稳定。对于卷积层而言，Din = (kernel_size ** 2) * input_channels。

Xavier 的推导：主要想法是我们希望输出的方差等于输入的方差。

但是如果我们是用 ReLU 作为激活函数，注意到 Xavier 假设的是零均值的激活函数，那么 Xavier 也会使得多轮后的激活结果趋近于零，依旧没有学习。解决方法是使用 Kaiming 初始化，定义为 W = np.random.randn(Din, Dout) / np.sqrt(Din / 2)。

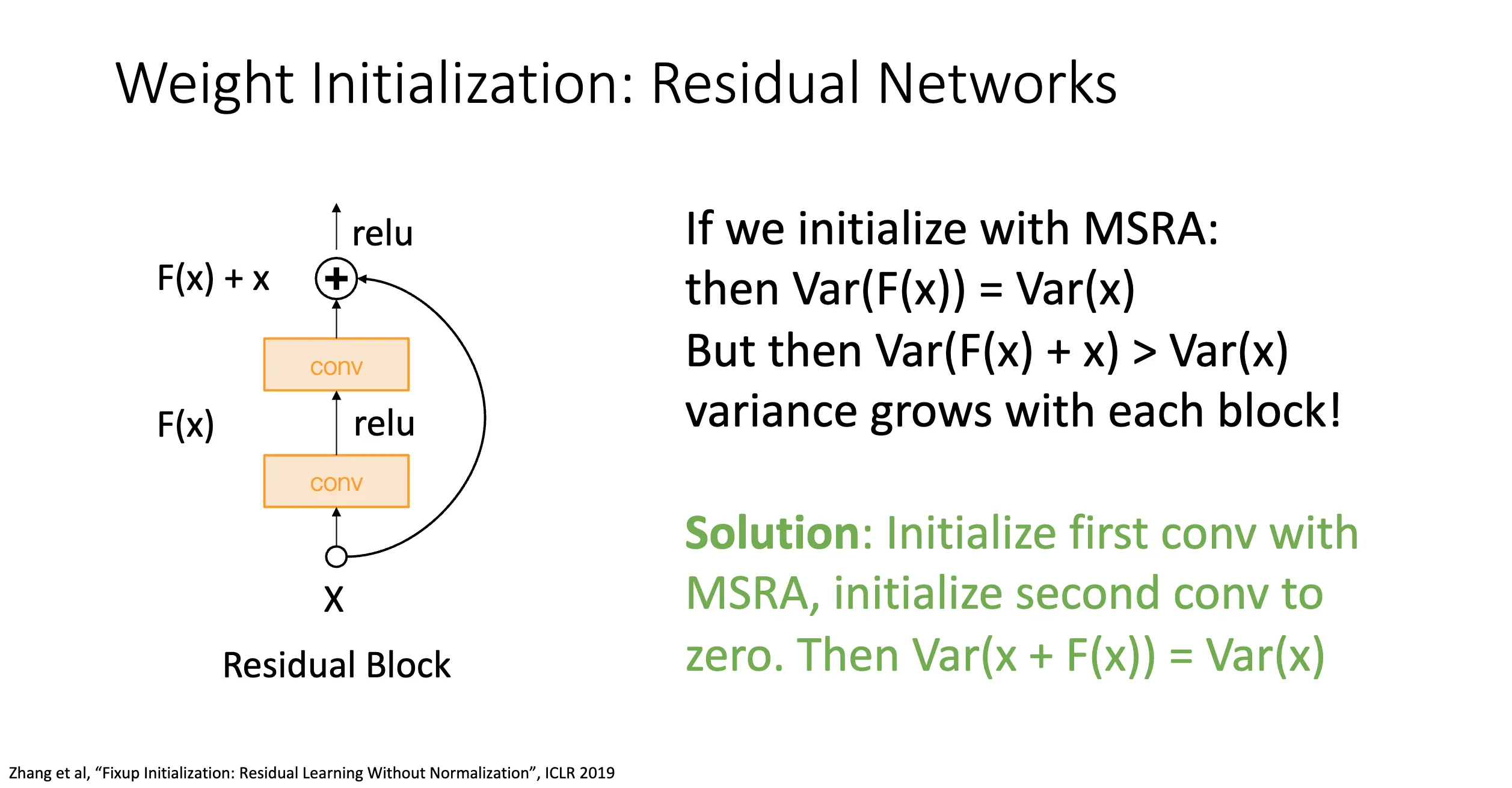
对于残差网络而言，如果我们还是使用 Kaiming 初始化，那么就有 \(\mathbb{V}[F(x)] = \mathbb{V}[x]\)，但是 \(\mathbb{V}[F(x) + x] > \mathbb{V}[x]\)，这会导致方差每一层单调严格增，导致梯度爆炸和严重的优化问题。解决方法甚至更简单，将第一个卷积层使用 Kaiming 初始化，让后面的一个卷积层初始化为 0。

正则化：如果我们的模型训练还挺好，但是训练误差和验证误差差别很大，这应该就是因为过拟合了，正则化是很好的解决方式：直接在损失函数中增加一个正项，令模型倾向于使用更小的权重。

  • \(L_1\) 正则化：\(R(W) = \sum_k \sum_l \lvert W_{k,l} \rvert\)；
  • \(L_2\) 正则化（权重衰减）：\(R(W) = \sum_k \sum_l W_{k,l}^2\)；
  • 弹性网络正则化：\(R(W) = \sum_k \sum_l (\beta W_{k,l}^2 + \lvert W_{k,l} \rvert)\)，其中 \(\beta\) 是一个超参数。

Dropout：正则化的一种。在训练的时候，使用一定的概率随机丢弃一些神经元，丢弃神经元的概率为 \(p\)，常见为 0.5。一种解释是强制神经网络提供冗余表示，防止特征的 Co-Adaptation。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
p: int = 0.5

def train_step(X):
    """X Contains the data"""

    H1 = np.maximum(0, np.dot(W1, X) + b1)
    U1 = np.random.rand(*H1.shape) < p
    H1 *= U1
    H2 = np.maximum(0, np.dot(W2, H1) + b2)
    U2 = np.random.rand(*H2.shape) < p
    H2 *= U2
    out = np.dot(W3, H2) + b3

    # backward pass
    # perform parameter updates

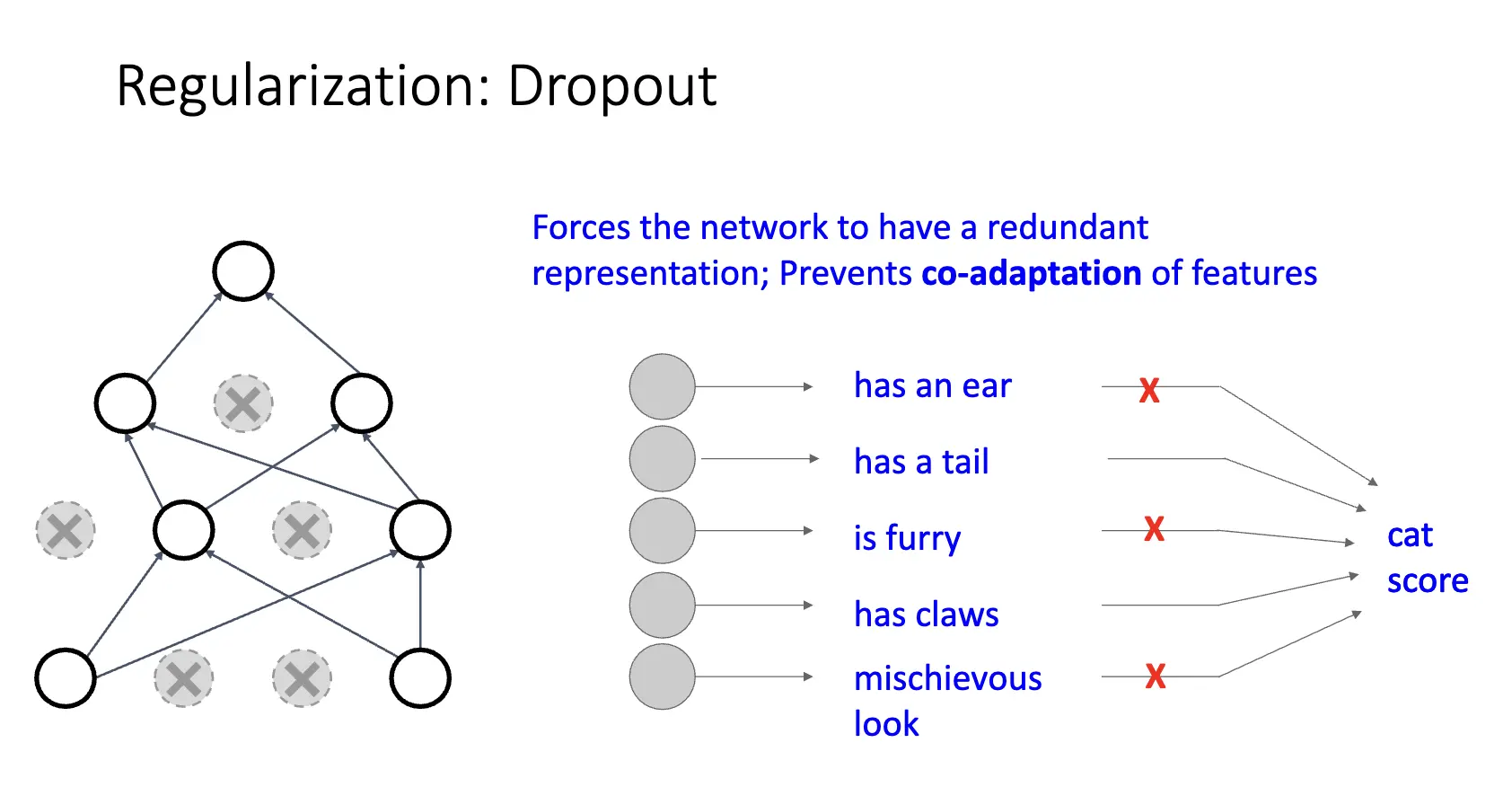
另一种解释是 Dropout 其实是在训练很多模型的一个大型集成，其中模型之间共享参数，这样，每一种可能的 Dropout 都对应着一个模型。

在测试的时候，似乎 Dropout 会给我们带来麻烦：由于 Dropout 引入了随机性：\(y = f_{W}(x, z)\)，其中 \(z\) 是随机的掩码，我们不希望输出的时候是不确定的，想法是对于所有 Dropout 引入的随机性取期望：

\[y = f(x) = \mathbb{E}_{z} \left[ f_{W}(x, z) \right] = \int p(z) f_{W}(x, z) \,\mathrm{d}z\]

但是很难计算积分（真的很难吗），解决方法是类比一个神经元的情景，在测试的时候我们不 Drop 任何一个神经元，但是我们把结果乘以我们 Dropout 的概率 \(p\) 就可以了。

1
2
3
4
5
6
7
p: int = 0.5

def predict(X):
    # ensembled forward pass
    H1 = np.maximum(0, np.dot(W1, X) + b1) * p
    H2 = np.maximum(0, np.dot(W2, H1) + b2) * p
    out = np.dot(W3, H2) + b3

更常见的是我们宁愿在训练的时候使用 Dropout 对参数进行缩放，在测试的时候不改变参数的值，这正好是出于测试效率着想：

在古早的网络，我们在最后的全链接层使用 Dropout，但是较为现代的网络使用全局平均池化，这就不需要使用 Dropout 了。

更通用的模式是在训练的时候引入随机性，在测试的时候对随机性进行平均/边缘化，比如我们的批归一化。

数据增强：对原始训练数据进行变换，创建更加多样的训练样本，同时保持图像的语义不变。

  • 水平反转；
  • 随机裁剪并缩放：以残差网络举例
    • 训练的时候我们选择随机边长，调整短边边长为选择的随机边长，然后随机采样 \(224\times 224\) 的区域；
    • 测试的时候分别将测试图片缩放到多个尺寸，对于每个尺寸在四个角和中心取样，对每个取样进行翻转，然后开始测试。
  • 颜色抖动/Color Jitter：
    • 简单处理：随机调整对比度和亮度；
    • 复杂处理：对所有 RGB 通道使用 PCA，在主成分方向采样一个颜色偏移/Color Offset，然后将其添加到所有像素上。
  • RandAugment：对图像应用随机组合的变换：
    • 几何变换：旋转、平移、剪切；
    • 颜色变换：锐化、对比度、亮度、曝光、颜色、Solarize、Posterize 等操作；
  • 分数池化/Fractional Pooling：
    • 训练的时候使用随机池化区域；
    • 测试的时候聚合多个样本的预测；
  • 随机深度/Stochastic Depth：
    • 训练的时候跳过残差网络的某些块；
    • 测试的时候使用整个网络；
    • 在最近（2022）的网络很流行；
  • 随机擦除/CutOut：
    • 训练时将图片的随机区域设为零或随机值；
    • 测试时使用完整图像；
    • 提高模型对部分遮挡的鲁棒性；
  • Mixup：
    • 训练时随机混合两个图像的像素，目标标签也按相同比例混合；
    • 测试的时候使用原来的图像；
  • CutMix：
    • 训练时将一个图像的随机区域替换为另一个图像，标签按照替换像素的比例混合；
    • 测试的时候使用原来的图像；
  • 标签平滑/Label Smoothing：
    • 将硬标签转为软标签；
    • 数学表示：正确类别设为 \(1-\frac{K-1}{K}\epsilon\)，其他类别设为 \(\epsilon/K\)，其中 \(K\) 是类别数，\(\epsilon\) 是一个很小的数，比如 0.1。

总结一下：

Lecture 10: Training Neural Networks II

Lecture 11: CNN Architectures II