Part 1: Lecture 1 to Lecture 6¶
约 1684 个字 21 张图片 预计阅读时间 6 分钟
Table of Contents
Lecture 1: Introduction¶
Lecture 2: Image Classification¶
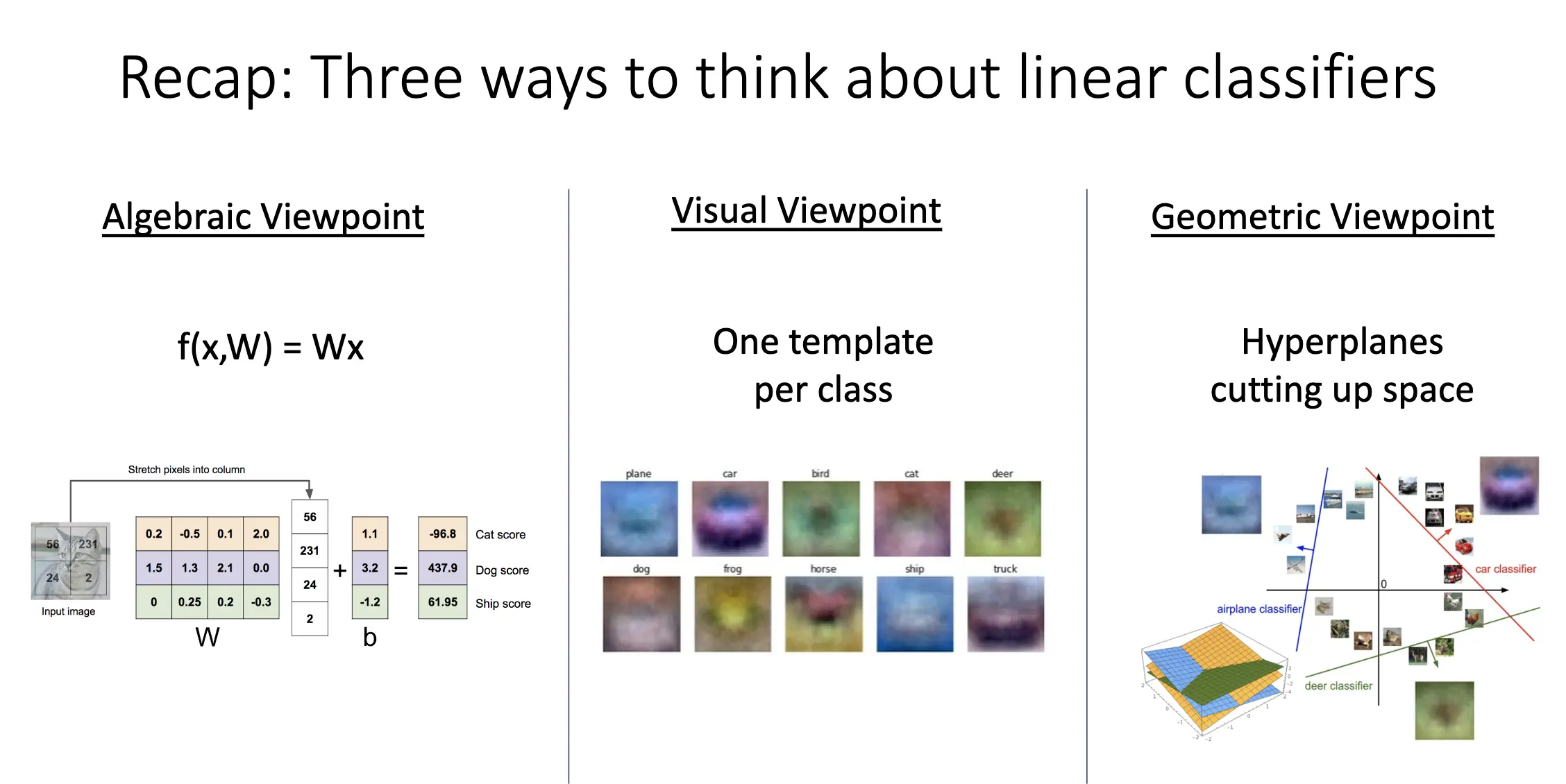
Lecture 3: Linear Classifiers¶
损失函数告诉我们当前的分类器性能有多好。训练集的损失是每一个样本损失的平均值。
- Softmax 损失:\(L_i = -\log \left( \dfrac{\exp(f_{y_i})}{\sum_{j} \exp(f_j)} \right)\)
- Multiclass SVM 损失:给定样本 \((x_i, y_i)\),令 \(s = f(x_i, W)\),则 \(L_i = \sum_{j \neq y_i} \max(0, s_j - s_{y_i} + \Delta)\)

Lecture 4: Regularization & Optimization¶
过拟合:模型在训练集上表现很好,但是在没见过的数据上表现惨淡,经验风险很低,泛化风险非常高。在机器学习理论的视角上看是算法在期望条件下不具有替换样本稳定性。
正则化/Regularization 是缓解过拟合的一个方法之一,在训练误差加入防止模型过于贴近训练数据的一项,这一项经常和模型本身的性质相关,比如模型参数的值。与其相关的还有正则化参数,其控制了正则化项的权重,这是一个超参数。

如果对于两套不同的参数,同样的输入会给出同样的输出,这时正则化项就表现出其对不同参数的偏好了,可以看下面的例子:

这时,损失函数就包含了数据损失(用来 fit training data)和正则化项(用来防止过拟合)。
现代常用梯度下降对函数进行优化,一般使用分析方法求解梯度,使用数值方法检验梯度(Gradient Check)

torch 有 torch.autograd.gradcheck 可以用来检验梯度。
Check gradient of gradients computed via small finite differences against analytical gradients w.r.t. tensors in
inputandgrad_outputsthat are of floating point type and withrequires_grad=True. This function checks that backpropagating through the gradients computed to givengrad_outputsare correct.
- 梯度下降:在相反梯度方向上迭代,超参数为初始化权重的方法、学习率与迭代的次数;
- 批量梯度下降:完全使用数据集上的所有数据进行迭代,当数据集很大时,计算量很大;
- 随机梯度下降:我们实现的是小批量梯度下降,每次使用一小部分数据进行迭代,超参数为权重初始化方法,迭代的次数、学习率、批量大小和数据采样方法。

可以使用加速方法,比如动量法,来加速梯度下降,提升稳定性。
Adam:结合了 RMSProp 和动量法,常见的四种方法(Momentum, Adaptive Learning Rate, Leaky Second Moments, Bias Correction)都使用了:

在新的问题中,我们可能使用 AdamW(Adam with Decoupled Weight Decay),正常的 \(L_2\) 正则化项是直接在损失函数上添加,Weight Decay 直接在优化器上添加。

诸如 L-BFGS 等二阶优化方法也很常见,但是这些算法在 Full Batch 并且确定性情况下工作得很好,但是在小批量情况下,这些算法就会给出不太好的结果。
Lecture 5: Neural Networks¶
问题之一在于,线性分类器并不是那么有效,正如我们学习感知机的时候,我们知道线性分类器只能处理样本可以被一个超平面有效分开的情况,对应也产生了支持向量机尤其是带有核方法的支持向量机等方法,我们也可以使用神经网络来解决这个问题。

像这种全链接的神经网络,我们又称为多层感知机。查看我们训练得到的模型对应的图片,我们发现模型可以使用多个不同的模版来覆盖同一类别的不同情况,同时很多模版其实是不可分辨的,因为其对应了不同的模型,这也是一种分布式表示。
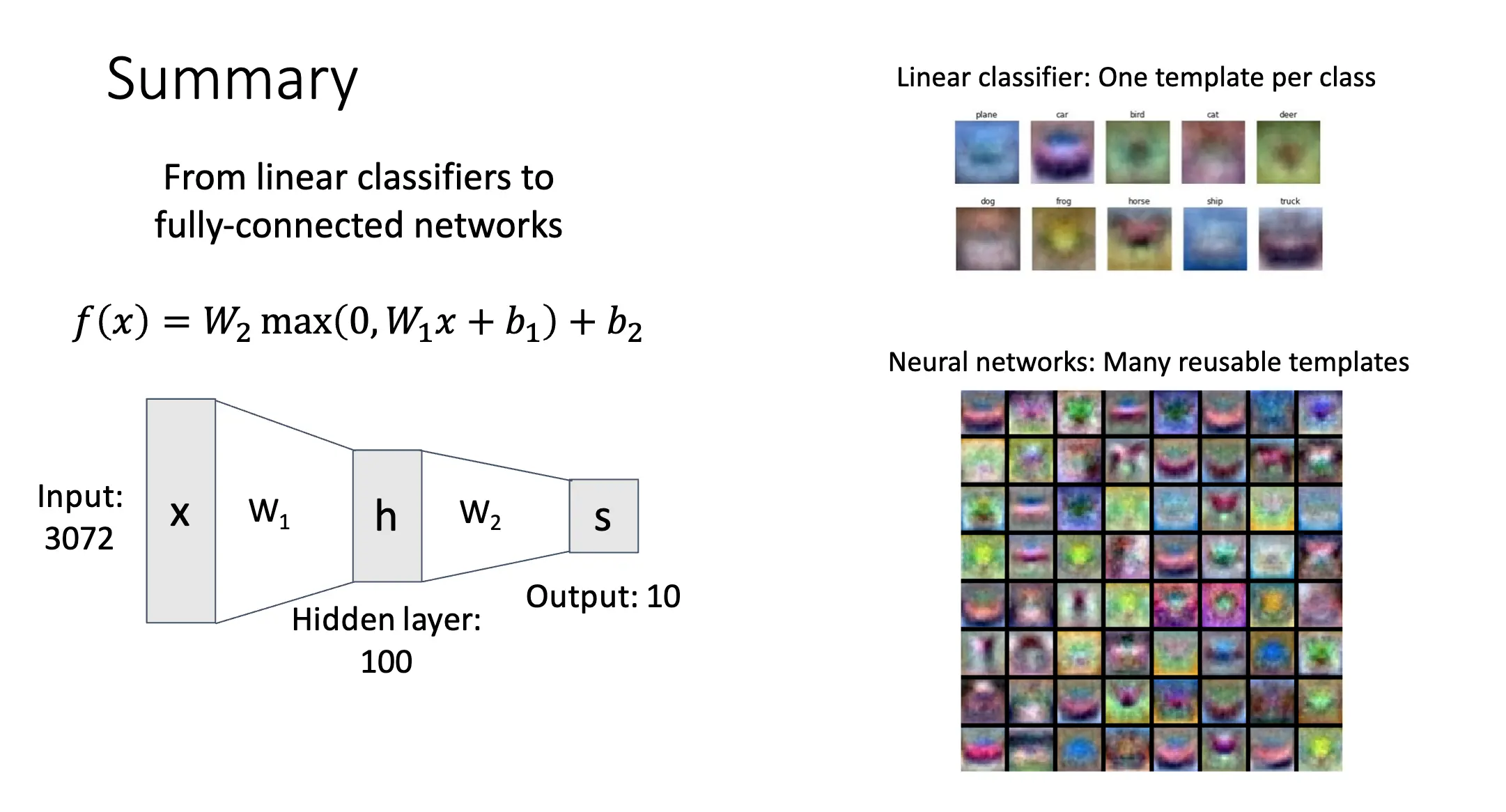
我们在神经网络表达式看见的 \(\max\) 函数其实被称为激活函数/Activation Function,常见的激活函数有 Sigmoid, ReLU, Tanh, Leaky ReLU, ELU, Softplus 等。对很多问题来讲,ReLU 就已经足够了。
这里有一个用很少行就实现简单的神经网络的正向传播的例子:
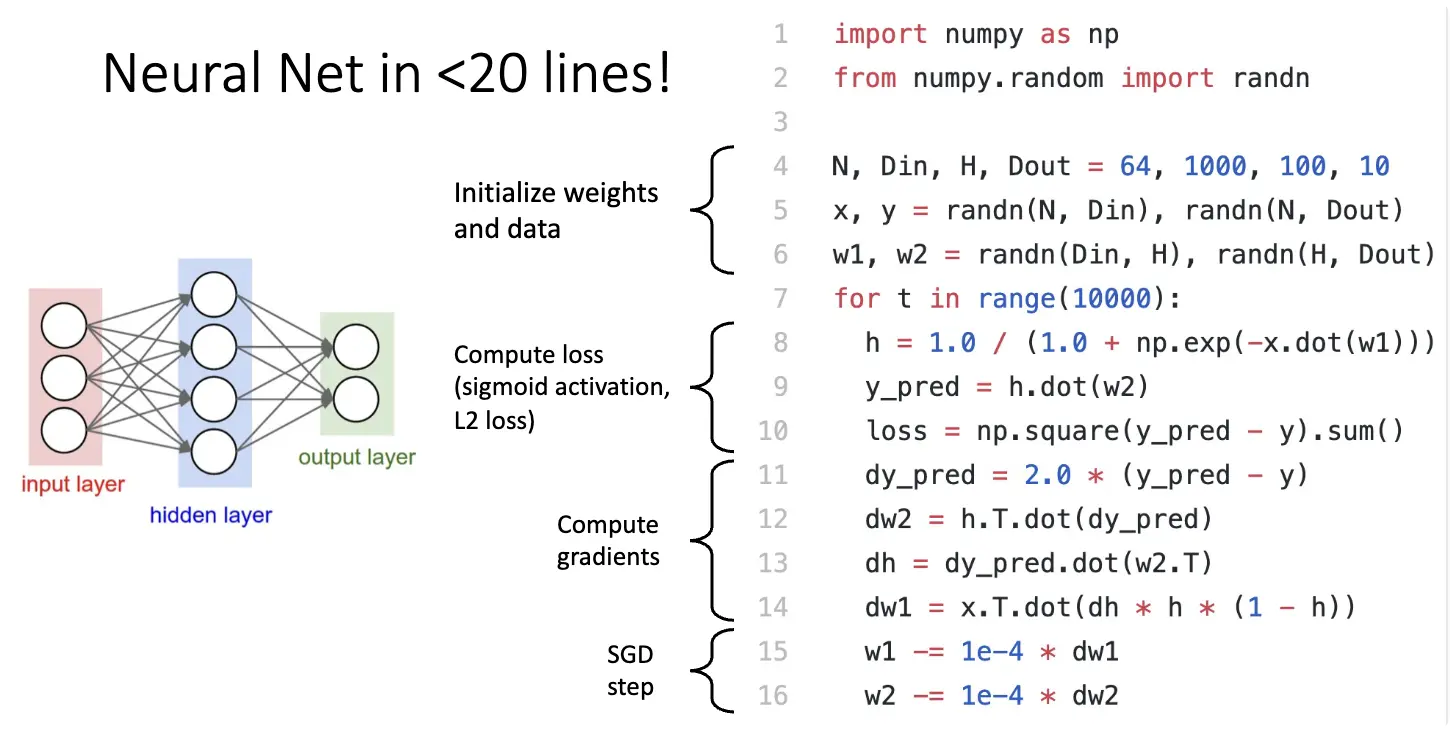
线性变换相当于改变样本点在空间中的位置,但是很难改变样本的线性可分性:

通过激活函数,我们可以对样本点的位置进行一个很微妙的改变,比如对于 ReLU 函数来说,我们就将第二、四象限的样本点挤压到了两个坐标轴上,将第三象限的样本点挤压到了原点。这样我们就可以将原本线性不可分的样本变得线性可分了:
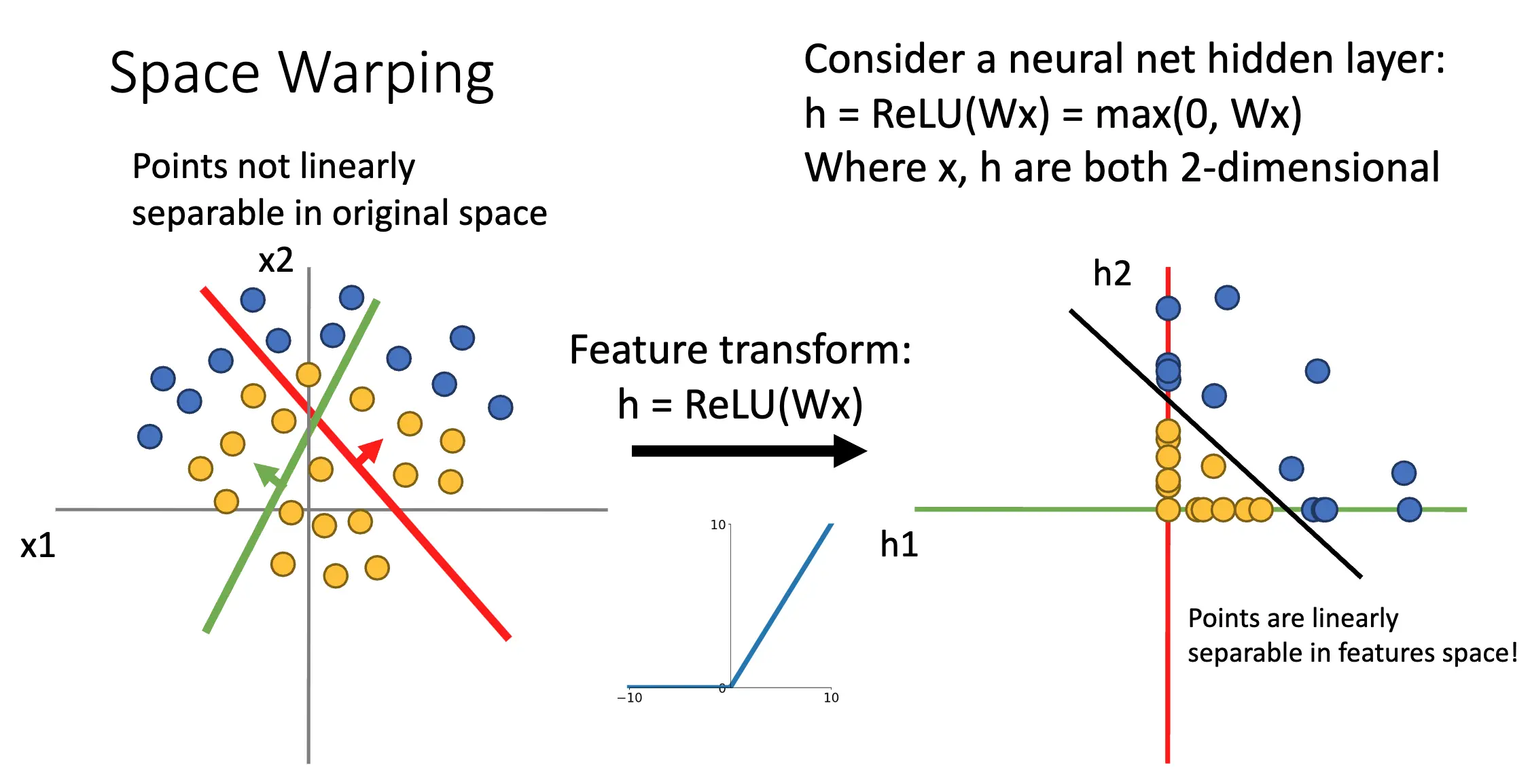
神经网络也有 Universal Approximation 性质,也就是神经网络可以拟合任何函数。但是这并未告诉我们,我们可以使用 SGD 学习任何函数,我们也不知道到底需要多少数据才可以学得一个函数。
Lecture 6: Backpropagation¶
想法:如果我们可以将梯度算出来,我们就可以使用 SGD 进行优化,但是问题在于梯度很难算,一堆矩阵乘法,改变损失函数之后所有的梯度都要重新计算,并且这不适用于深一点复杂一点的模型。因此我们希望找到一种方法,通过结果反推出梯度。
更好的想法是使用计算图:
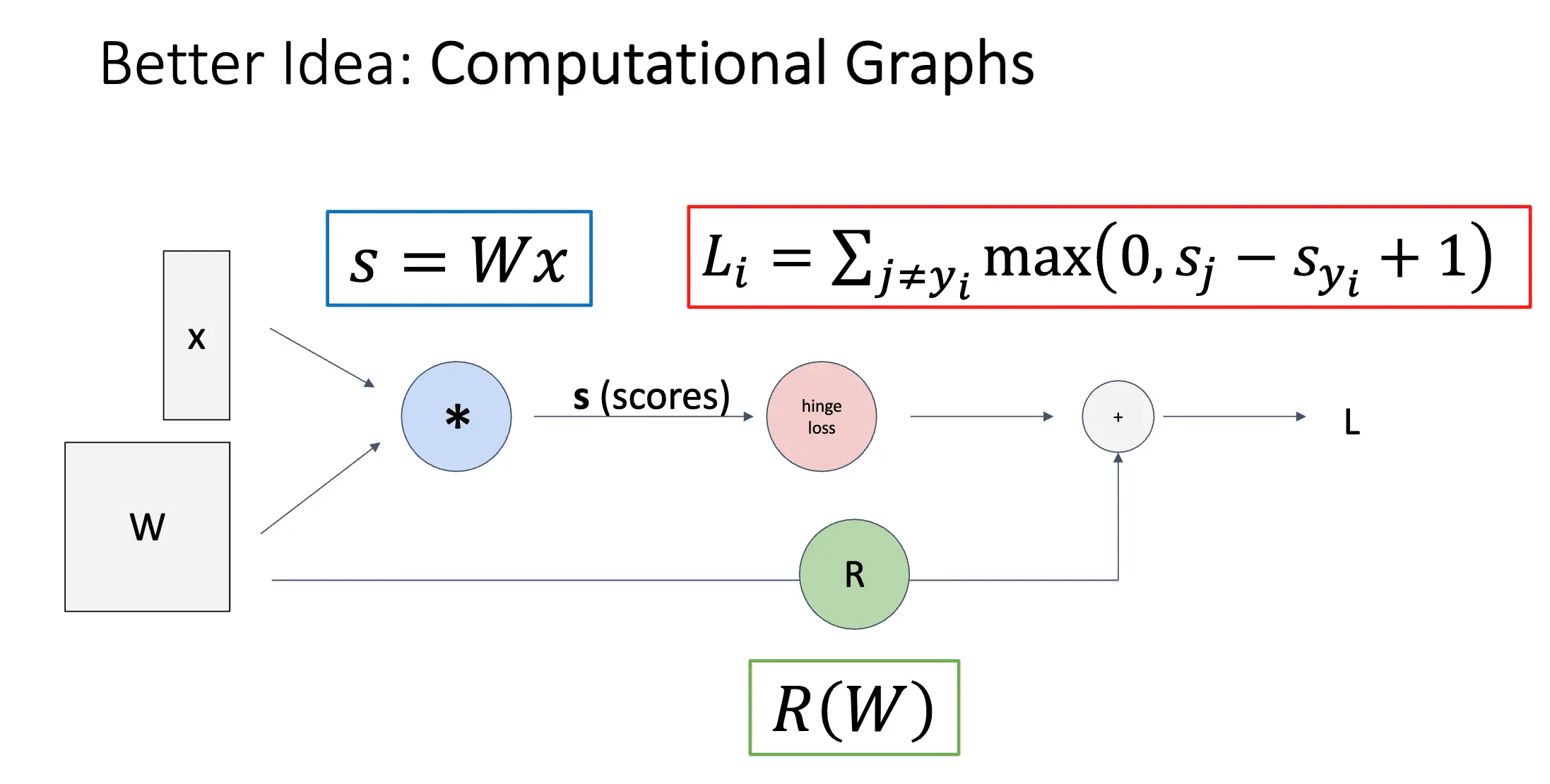
计算图可以很好的实现反向传播,图本身描述的就是正向传播的内容,反向传播就是通过链式法则,从后往前推导出梯度。图中流动的是梯度,我们在计算目标梯度的时候只需要将当前的梯度乘以流上去的剩下的梯度就可以了。
During the backward pass, each node in the graph receives upstream gradients and multiplies them by local gradients to compute downstream gradients.
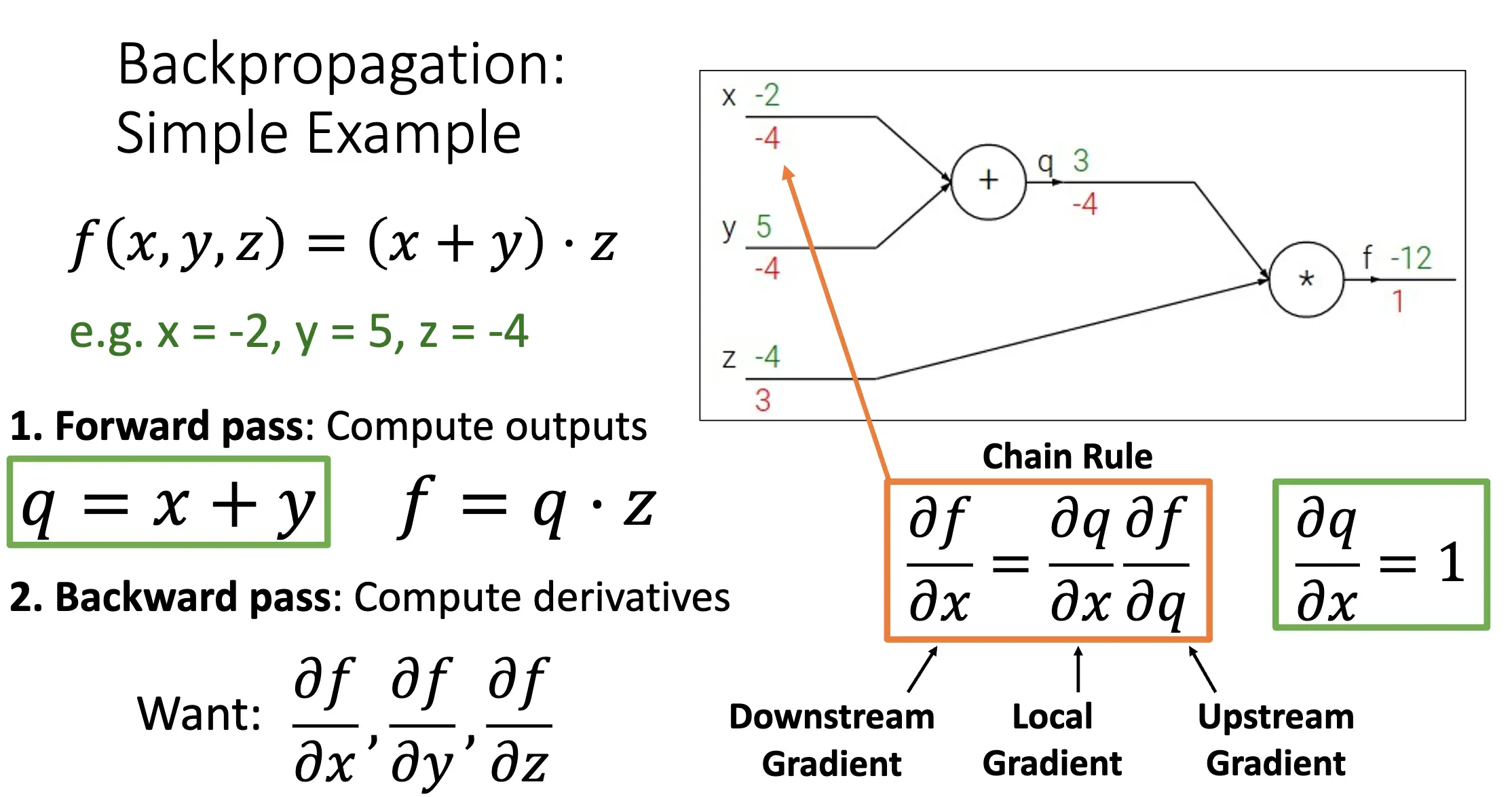
下面一图是对 Local Gradient、Upstream Gradient、Downstream Gradient 的解释:
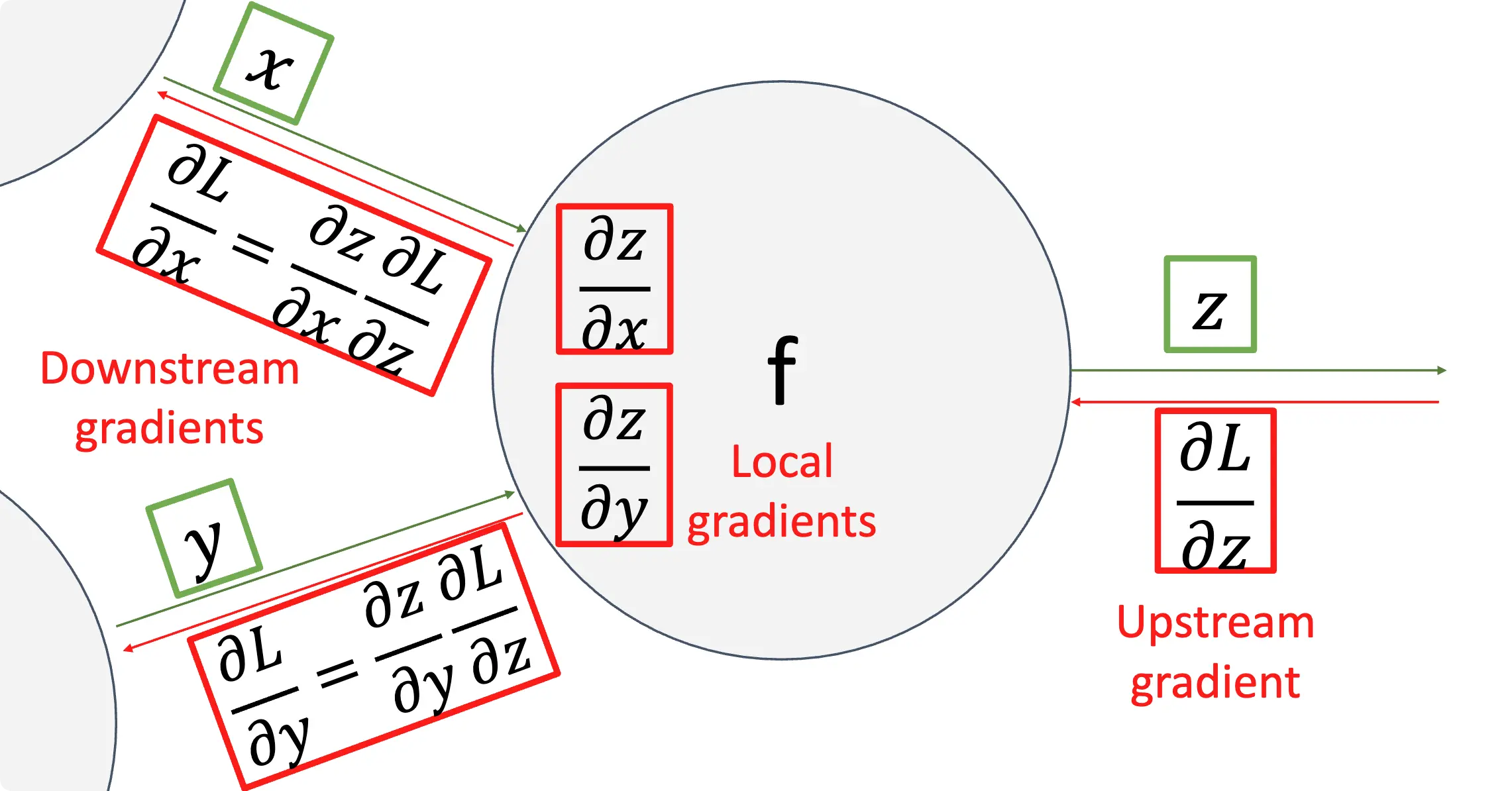
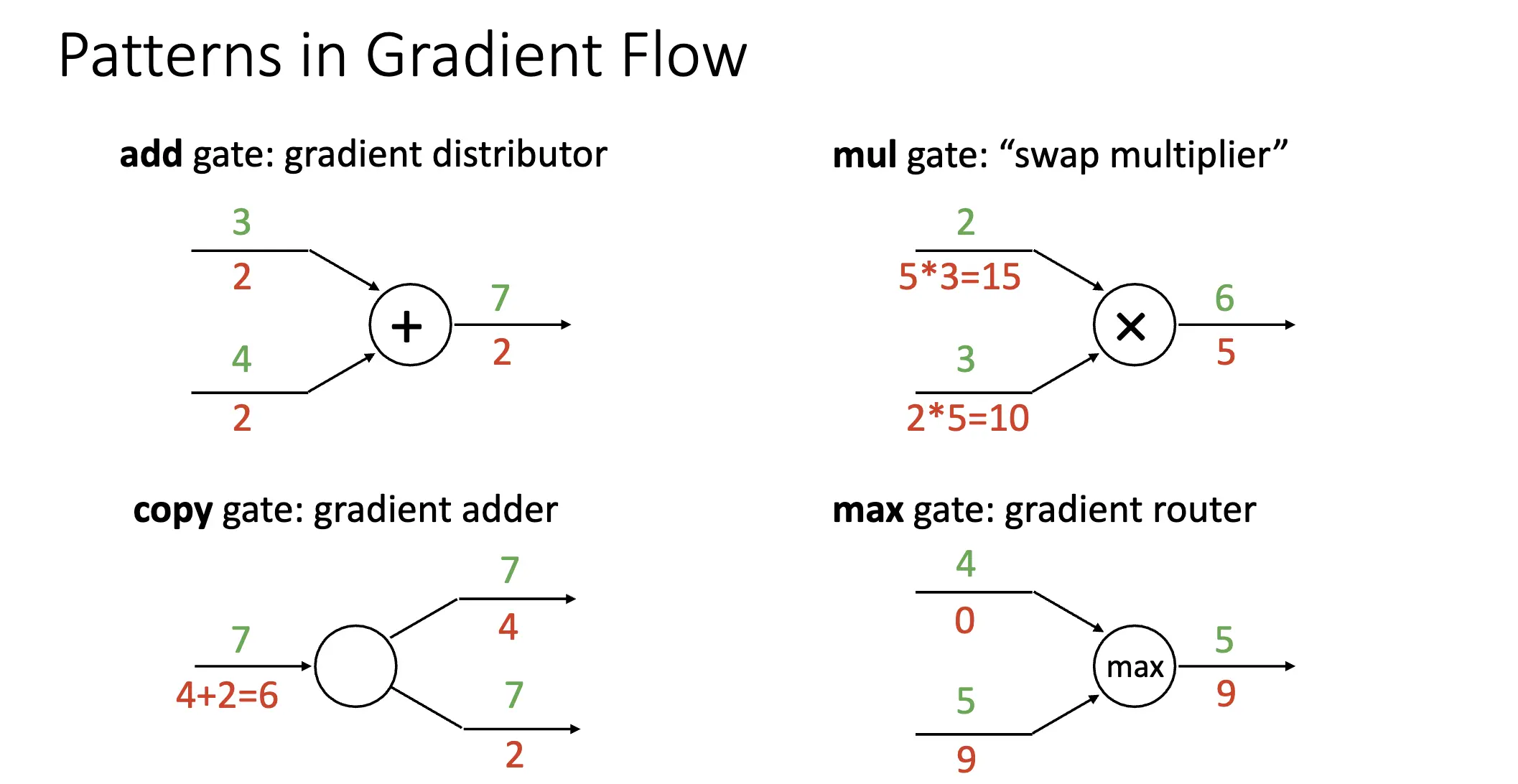
在计算图中,每一个节点可以看作一个门,每一个门对流下来的梯度进行了再分配:
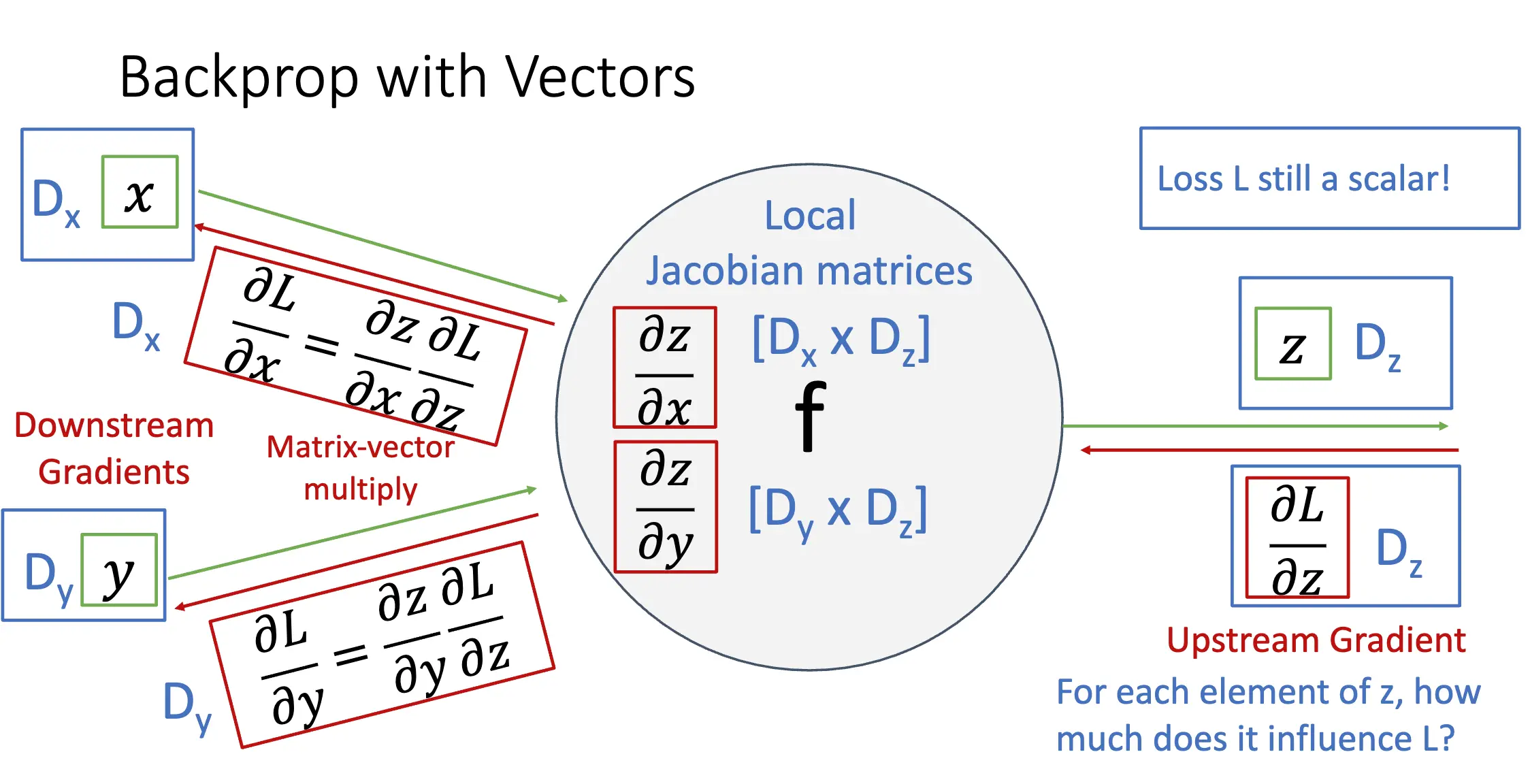
向量值函数:对于标量的函数,导数就是正常求导;自变量为向量,导数就是梯度;自变量和因变量都是向量,导数就是雅可比矩阵。这里的雅可比矩阵的定义和我们在分析学中学到的定义有所不同,也就是做了一个转置:

标出维数之后,反向传播的过程就不言自明了:
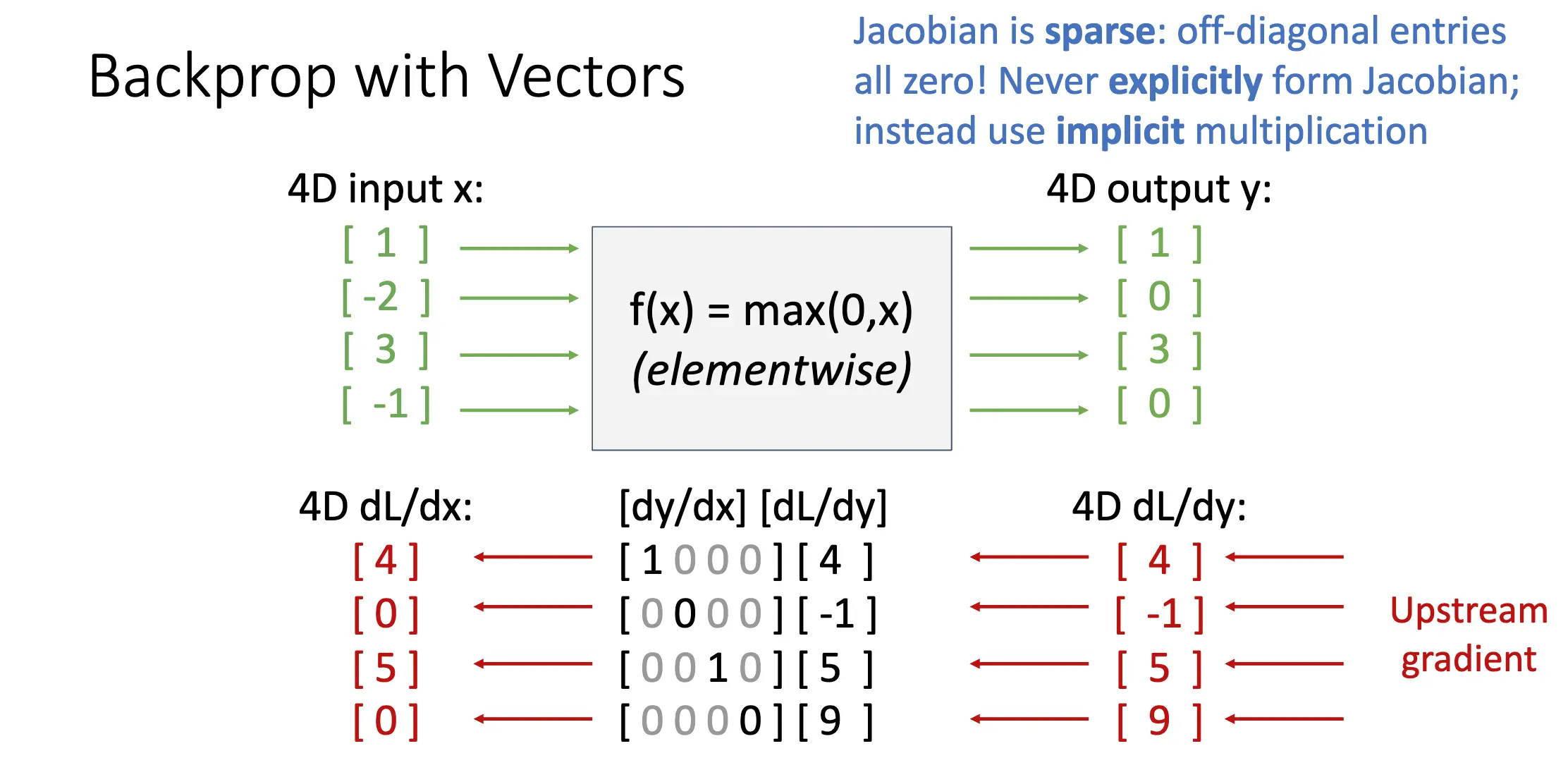
对于矩阵也是一样的: