跳转至

Part 4: Lecture 16 to Lecture 18

约 3817 个字 3 行代码 29 张图片 预计阅读时间 13 分钟

Table of Contents

Lecture 16: Recurrent Neural Networks

迄今为止，我们使用的都是前馈神经网络，输入和输出是一对一的关系。但是对于很多情况，比如序列输入或者输出，以及神经网络需要与时间序列相关的信息，前馈神经网络就无能为力了，因此我们引入循环神经网络/Recurrent Neural Network/RNN。简单结构与分类如下：

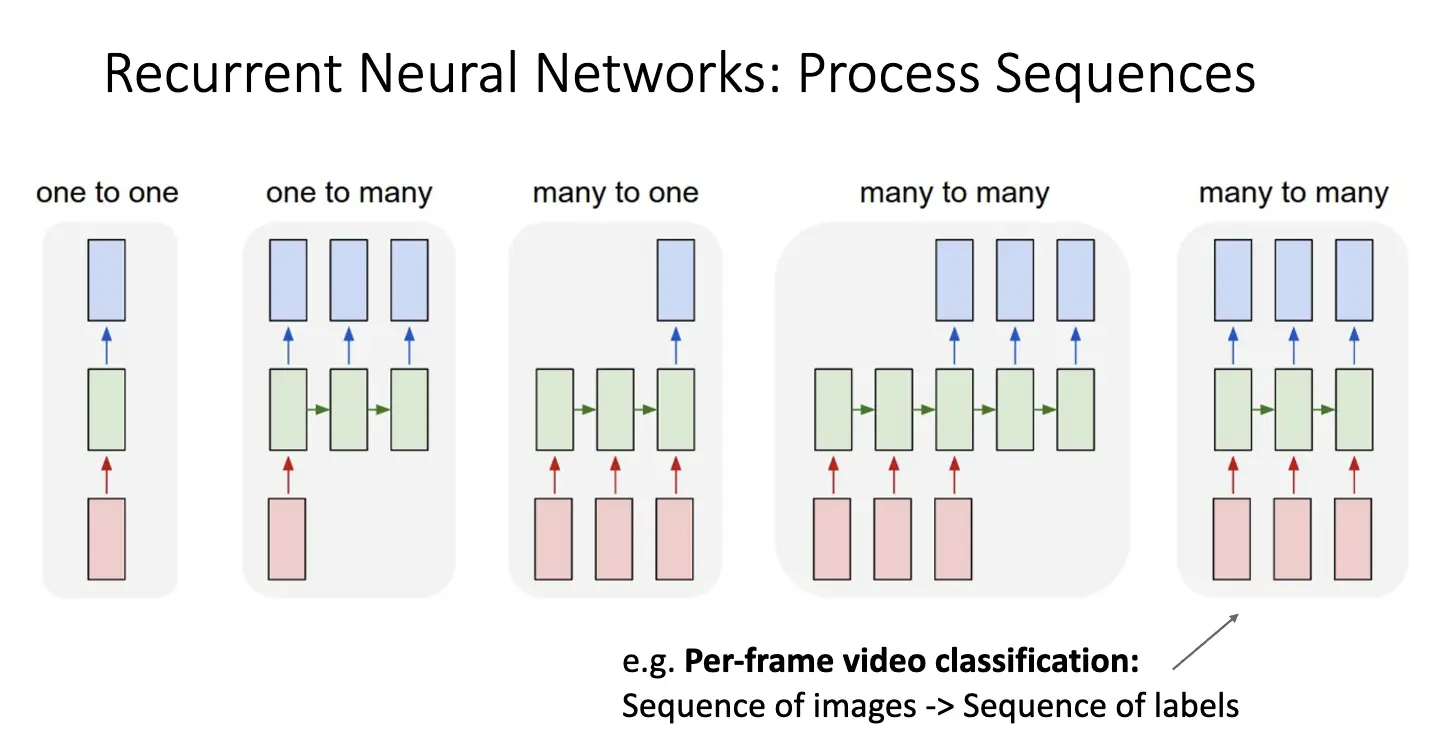
  • 一对一：比如图像识别任务，Image -> Label；
  • 一对多： 例如图像描述任务，Image -> Description (Sequence of Words)；
  • 多对一：比如视频分类任务：Sequence of Images -> Label；
  • 多对多：比如机器翻译任务，Sequence of Words -> Sequence of Words；

循环神经网络的核心想法是对一个向量在每一步应用相同的循环公式，其生成的新状态都和旧状态和当前输入相关：

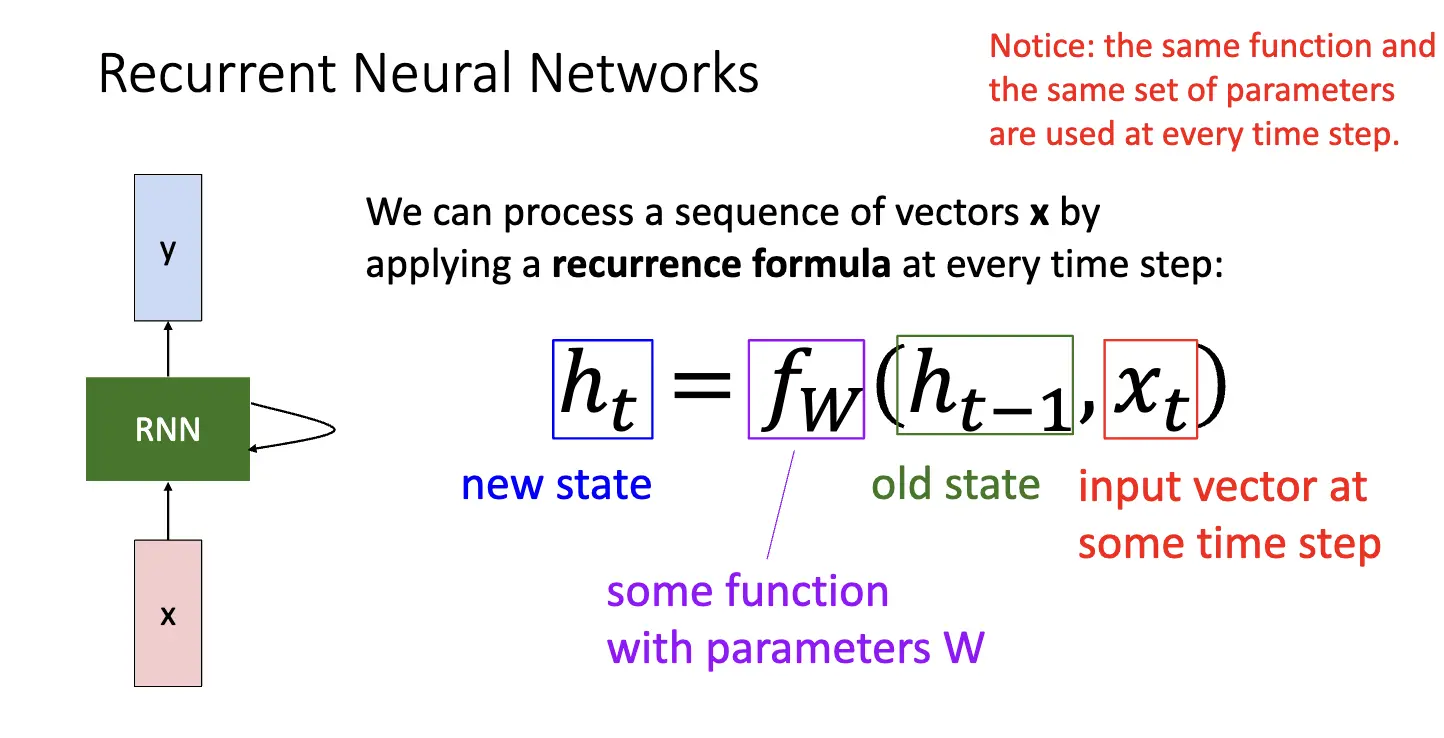
RNN 的计算图如下，对于 Many to Many 的情况，我们需要在每一个时刻根据当前状态和输入计算出下一个时刻的隐藏状态，并且根据隐藏状态计算出输出。这种情况的损失计算方法为：对每一时刻的输出计算损失再求和。

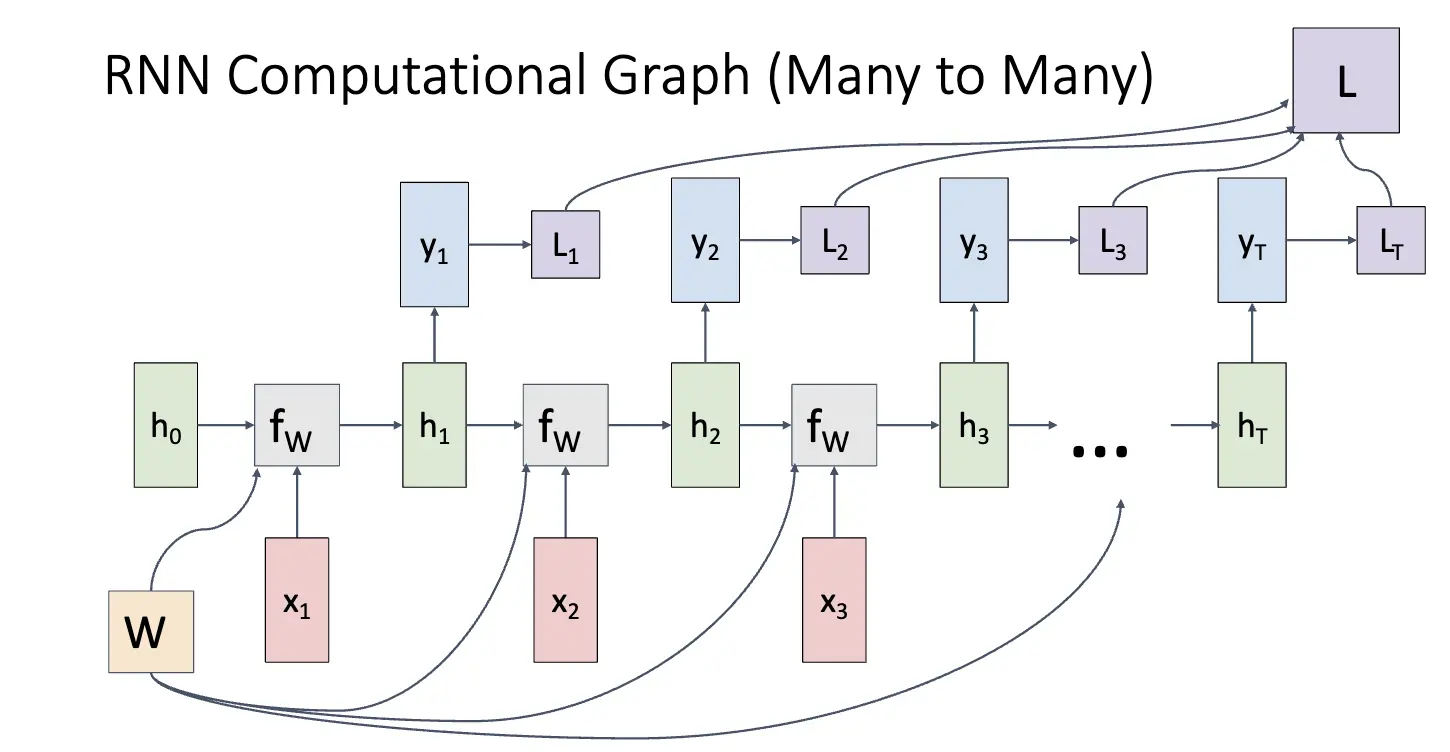
对于 One to Many 的情况，我们只需要根据输入利用循环方程不断更新隐藏状态，直到生成足够多的输出。对于 Many to One 的情况，我们只需要在最后一步利用隐藏状态计算出输出。

Many to Many 的情况可以拆分成 Many to One 的情况和 One to Many 的情况，这种也被称为 Sequence-to-Sequence 模型。前半部分将输入序列编码成一个向量，也称这部分为编码器/Encoder；后半部分从一个输入向量产生输出序列，也称这部分为解码器/Decoder。

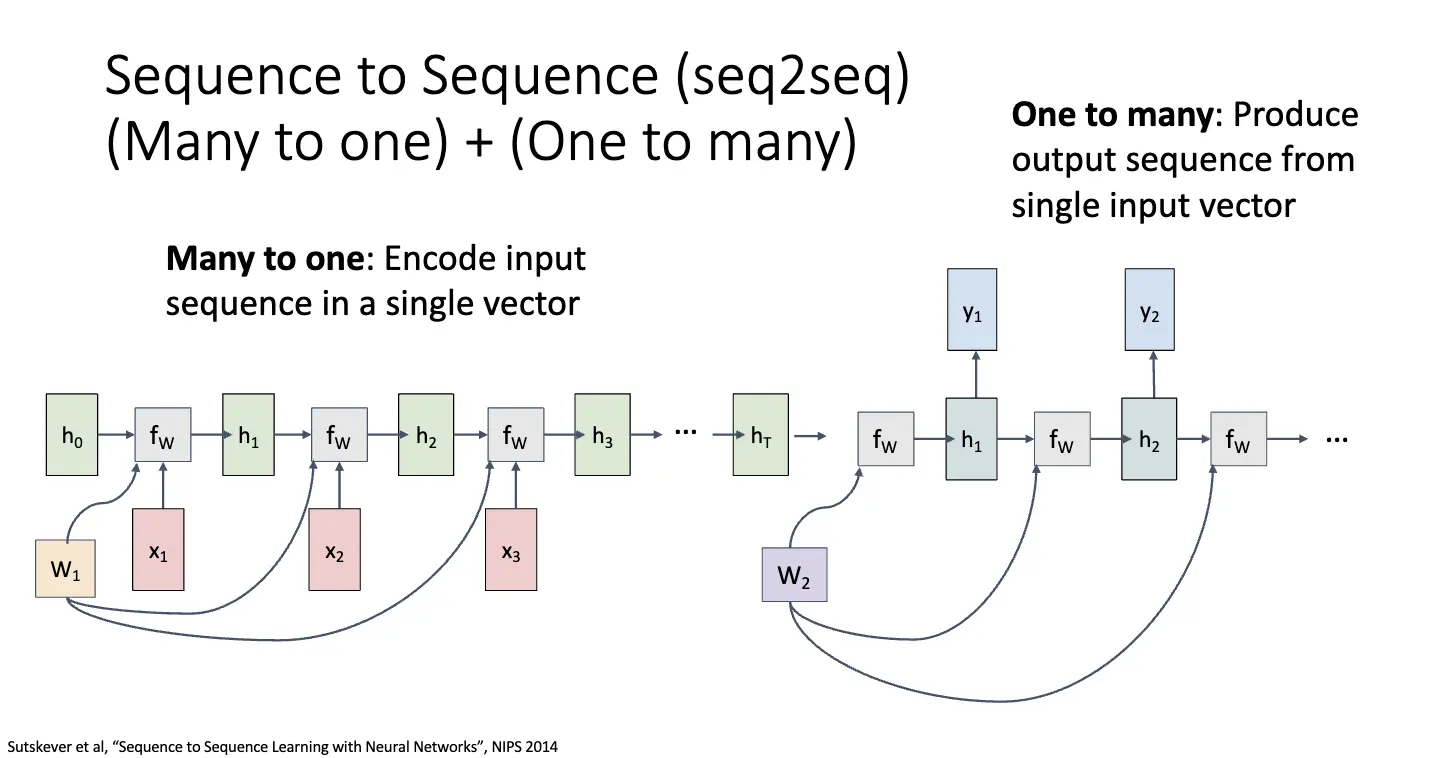
Language Modeling 是一个经典的问题，具体细节暂且不表，需要注意的是输入的处理：一个经典的想法是将输入编码为独热码，但是这会使得输入矩阵过于稀疏，并且难以处理长序列。因此我们使用词嵌入/Word Embedding 来将输入编码为密集向量。

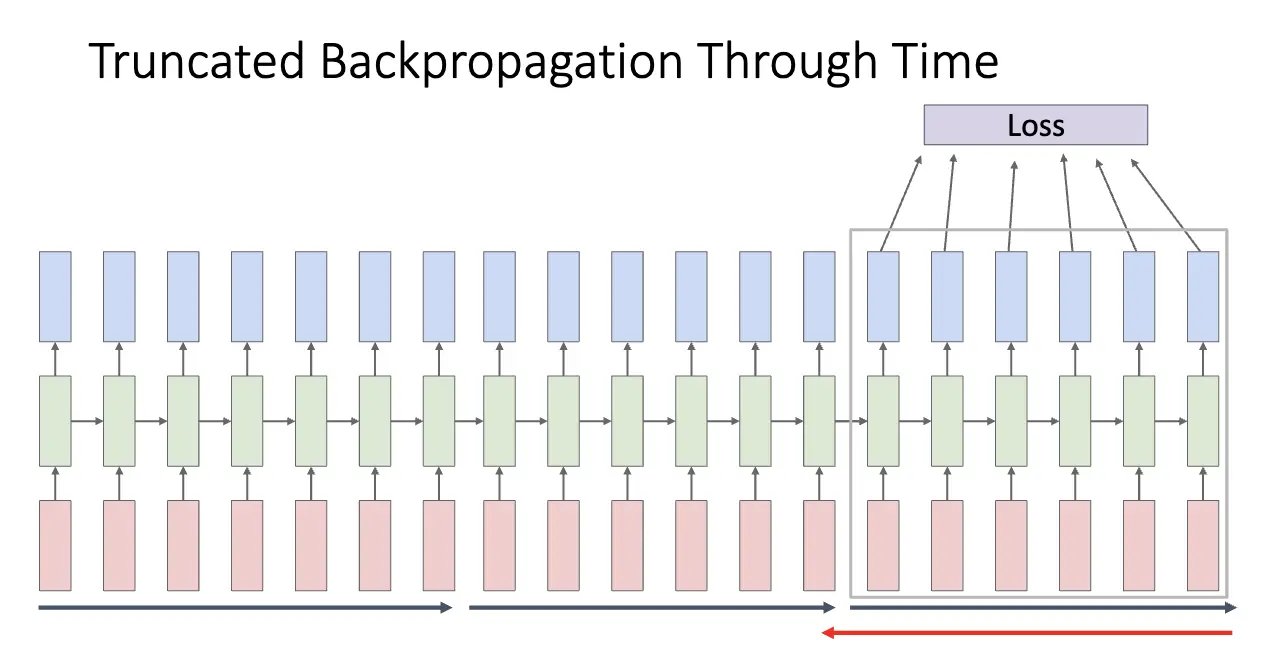
RNN 的反向传播也是一个问题，问题来自于其结构：对于循环公式而言，我们需要将梯度从当前状态传播到前一个状态，也就是沿着时间展开 Back Propagation Through Time/BPTT。注意到如果我们在自然语言处理领域处理长序列，我们可以很容易达到非常长的序列，比如你正在看的这篇笔记到这里已经有了两万余字符，这样展开的 RNN 就会非常深，因此需要考虑一下如何处理。大概想法是 Truncated BPTT，也就是只展开一小段时间，然后进行反向传播。

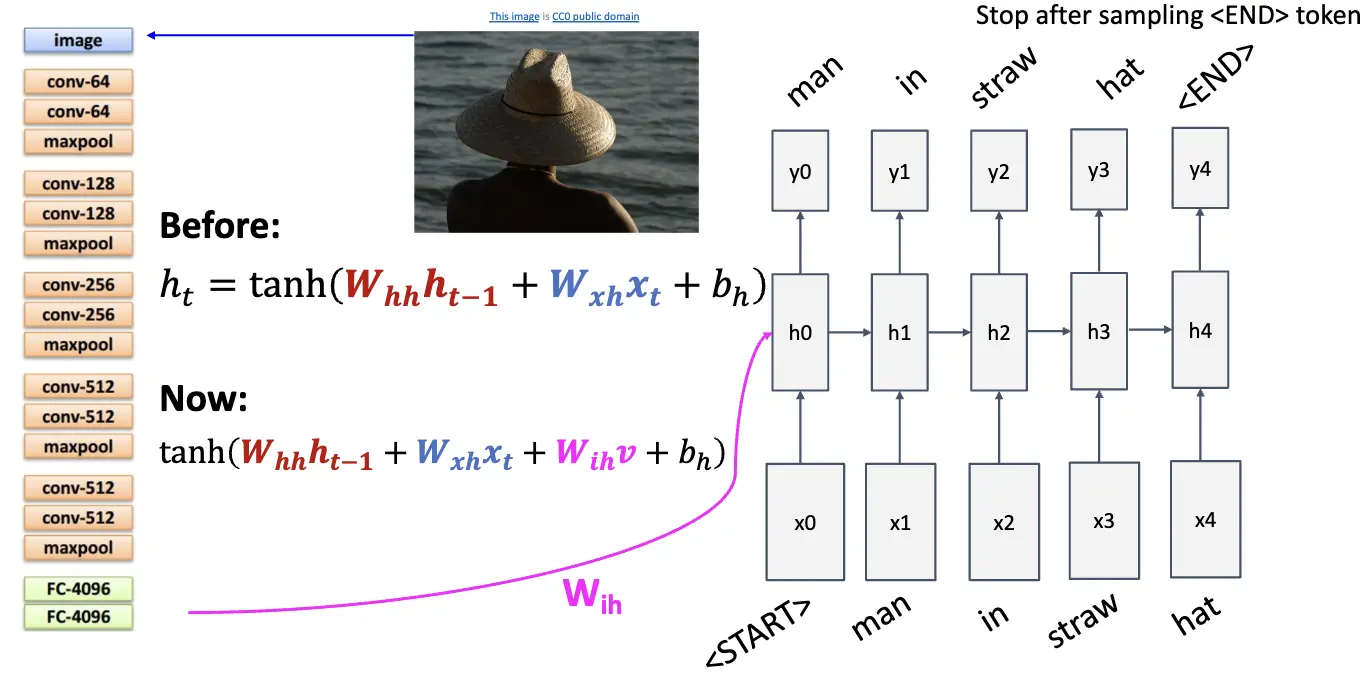
下图是一个 Image Captioning 的例子，输入是一张图片，骨干网络输出一个特征图，将特征图喂给 RNN 生成描述。

对于经典的 Vanilla RNN 有

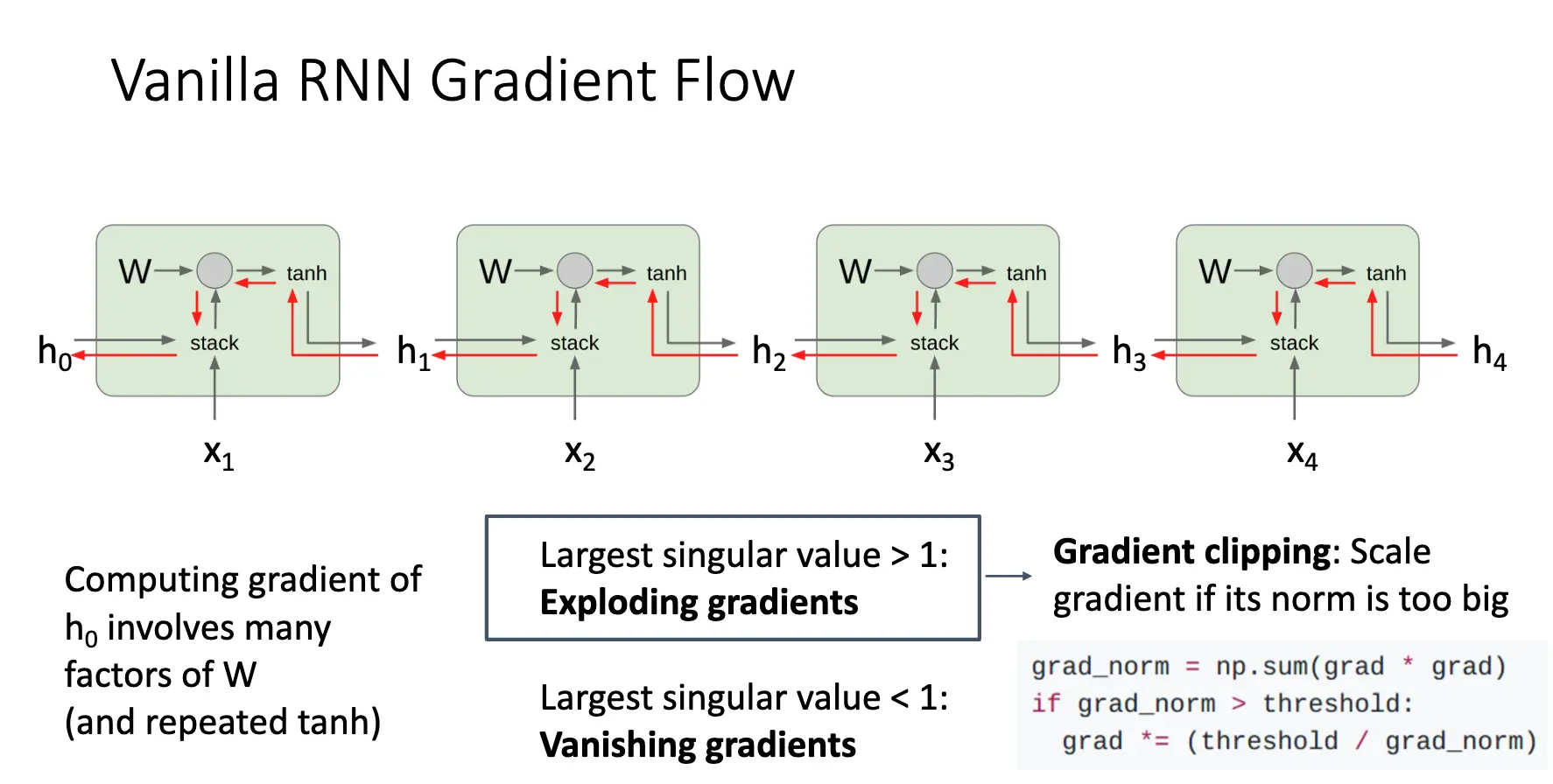
\[\begin{aligned} h_t &= \tanh(W_{hh} h_{t-1} + W_{xh} x_t + b_h) \\ &= \tanh \left( (W_{hh} \quad W_{xh}) \begin{pmatrix} h_{t-1} \\ x_t \end{pmatrix} + b_h \right) \\ &= \tanh \left( W \begin{pmatrix} h_{t-1} \\ x_t \end{pmatrix} + b_h \right). \end{aligned}\]

可以看到，当我们对 \(h\) 进行反向传播的时候，每一步都会乘以一个 \(W_{hh}\)，当层数一多，就会出现两种问题：

  • 梯度爆炸/Gradient Exploding：来自于 \(W_{hh}\) 的最大特征值大于 1，解决方法是梯度裁剪/Gradient Clipping，如果梯度太大了，就对梯度进行缩放：

    1
2
3
    grad_norm = np.sum(grad * grad)
if grad_norm > threshold:
    grad = grad * threshold / grad_norm

  • 梯度消失/Gradient Vanishing：来自于 \(W_{hh}\) 的最大特征值小于 1，解决方法只能是修改 RNN 架构，比如下面的长短期记忆网络/Long Short-Term Memory/LSTM：

Info

很经典的一篇 Blog：Understanding LSTM Networks 中提到：LSTMs are explicitly designed to avoid the long-term dependency problem.

LSTM 架构在每一个时间点考虑两个向量：Cell State 和 Hidden State，和四个门：Input Gate、Output Gate、Forget Gate、Update Gate。

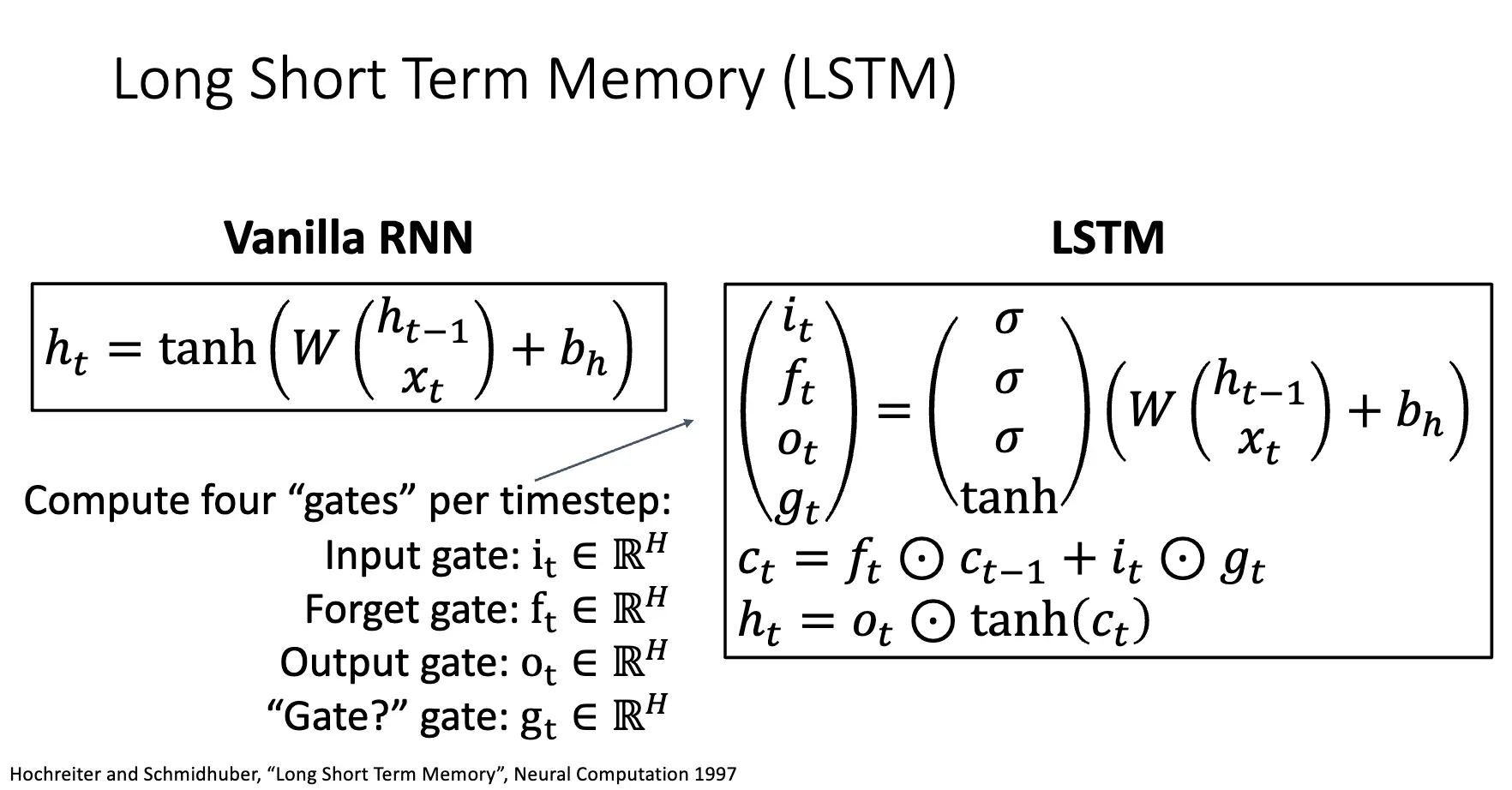
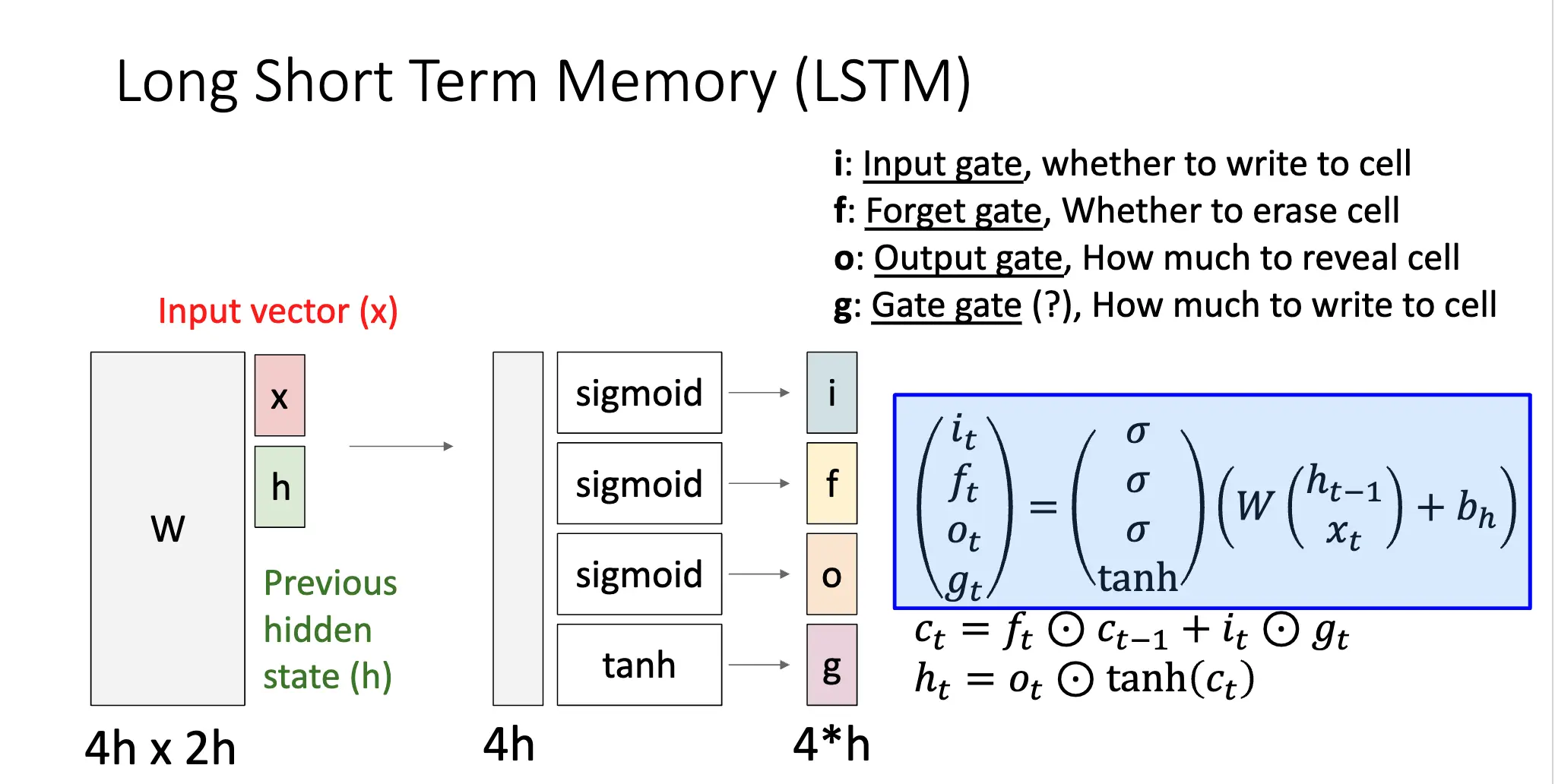
分析梯度流可以发现，对 \(C_t\) 的梯度流会直接流经 \(C_{t-1}\)，记忆单元直接在时间步之间传递信息，这是因为 \(C_t\) 是直接将 \(C_{t-1}\) 和 \(f_t\) 进行逐位相乘得到的，因此反向传播只需要执行加法，也就是不会出现梯度消失的问题。这样的设计也很类似 ResNet 的残差连接部分。

上述聊的是单层的 RNN，还可以设计更复杂的多层 RNN，比如下面的双层 RNN 就是将一个单层 RNN 的输出作为另一个单层 RNN 的输入：

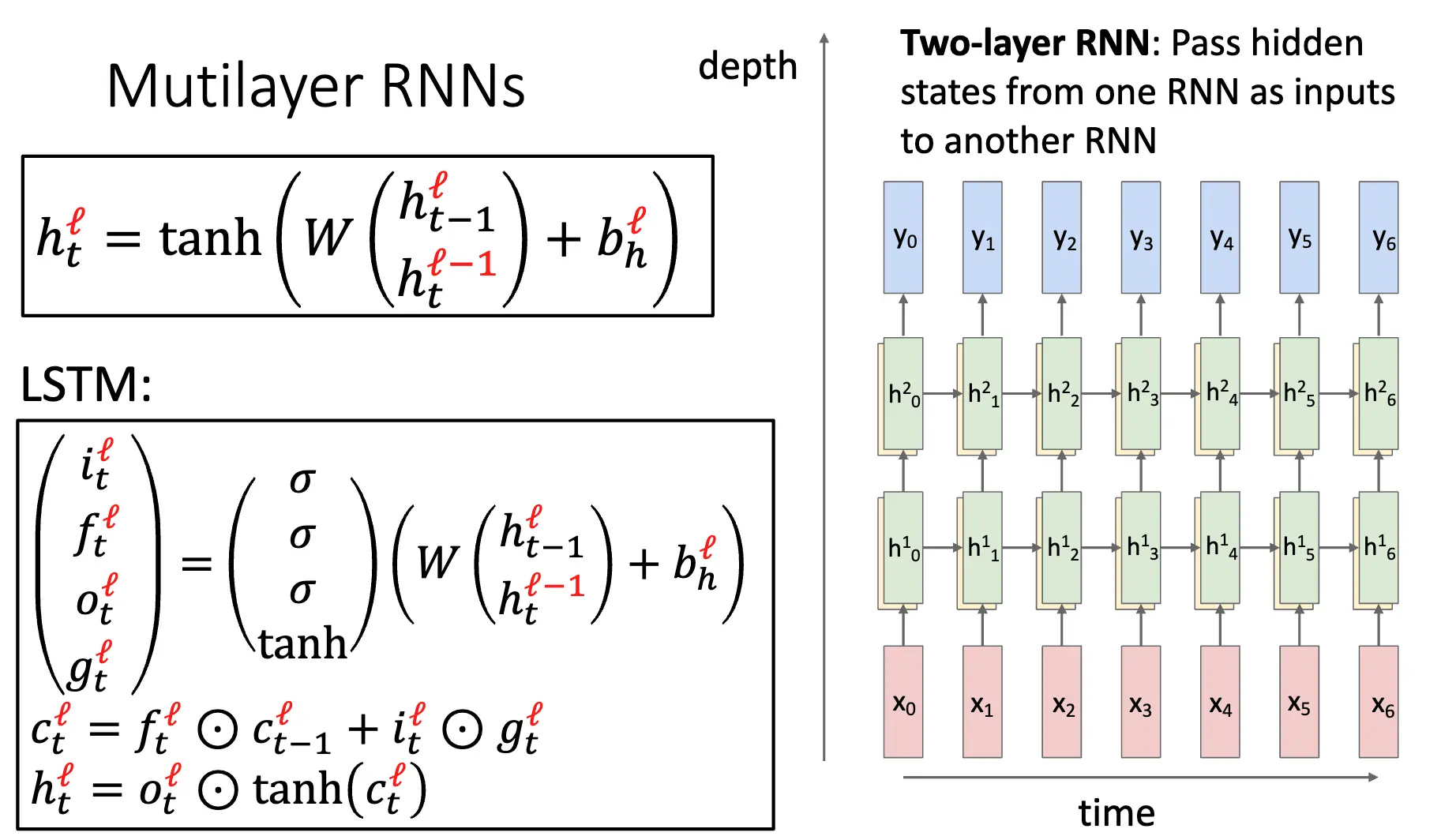
另一个变种是门控循环单元/Gated Recurrent Unit/GRU，结构更加简单，只有两个门：Reset Gate 和 Update Gate，并且将 Cell State 和 Hidden State 合并为单个状态。

Lecture 17: Attention

这部分也有参考 Stanford CS231N 的课程，两门课基本同根同源

回忆我们之前的 Seq2Seq 模型，整个模型可以拆分为 Encoder 和 Decoder 两个部分，中间通过一个固定长度的上下文向量传输信息。这样一来，这个上下文向量需要在某种程度上总结输入序列的所有信息，并且每次都喂给解码器一个相同的上下文向量，这显然是不合理的。

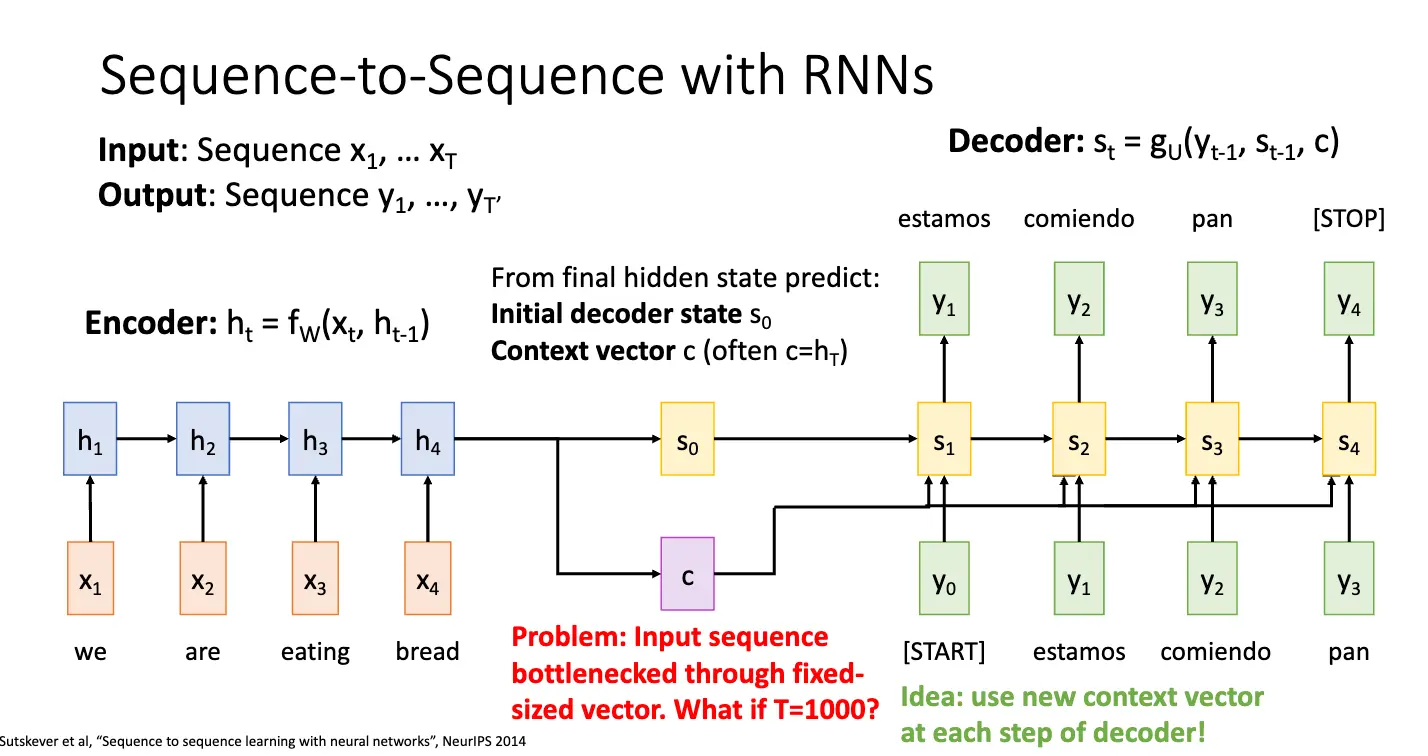
因此我们就需要引入注意力机制/Attention，基本架构还是差不多，还是 Encoder 和 Decoder 两个部分，但是我们对上下文向量进行了一些调整，基本想法是：将当前编码器的状态 \(h_i\) 和当前隐藏层状态 \(s_0\) 进行比较，计算出对齐分数 \(e_{t, i} = f_{\text{att}}(s_{t-1}, h_{i})\)，对齐分数指出输入序列和当前解码器状态的相似度，然后使用 Softmax 函数进行归一化权重 \(\alpha_{t, i}\)，将其转化为概率分布，最后将这些权重乘以编码器的状态 \(h_i\) 并求和得到当前输入解码器的上下文向量 \(c_t\)。

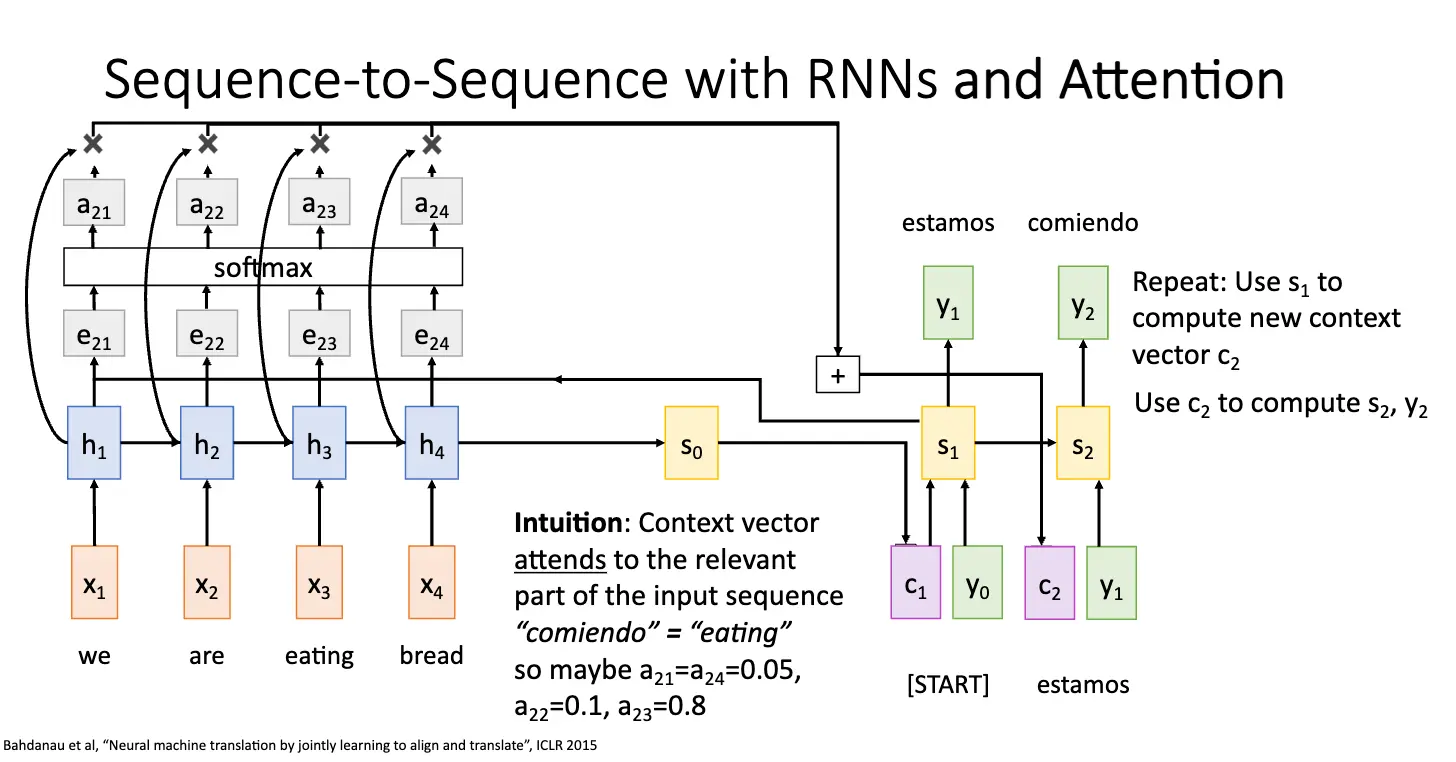
这个过程是动态的，比如对第一次输入，解码器的最初状态被设置为编码器的最终隐藏状态，那么我们传入函数 \(f_{\text{att}}\) 的参数就是解码器的最初状态和编码器的对每一个状态 \(h_i\) 的隐藏状态。当我们再一次输入的时候，解码器的隐藏状态被设置为上一次计算出的隐藏状态，然后我们传入函数 \(f_{\text{att}}\) 的参数就是解码器的隐藏状态和编码器的对每一个状态 \(h_i\) 的隐藏状态。

在解码器的每一个时间步都使用一个不同的上下文向量解决了输入序列被编码成单一固定长度向量的瓶颈问题；另一方面，上下文向量自动地看向输入序列的不同位置，因此也解决了输入序列中不同部分的重要性不同的问题。注意力机制是完全可微的，因此我们不需要监督网络，不需要告诉它输入序列中哪些词是必需的。相反，这只是一个由可微操作组成的大型计算图，所有这些都可以通过梯度下降端到端学习，网络会自行学习如何关注输入序列的不同部分。

值得注意的是，解码器并没有用到编码器状态 \(h_i\) 其实来自于一个有序序列的事实，只是将其当成来自一个无序的集合。因此我们可以将类似的架构用于任何输入的隐藏向量集合。

当我们从事计算机科学的研究的时候，如果发现一个东西很好用，那么一个自然的想法就是将其抽象化，然后推广到更一般的情况。于是我们开始设计注意力层。首先思考注意力机制的作用：

  • 数据向量：代表编码器 RNN 的隐藏状态，是我们需要总结的数据。
  • 查询向量：代表解码器 RNN 的隐藏状态，是我们需要输出的内容，查询向量需要回溯查看数据向量，将数据向量信息汇总成一个上下文向量。

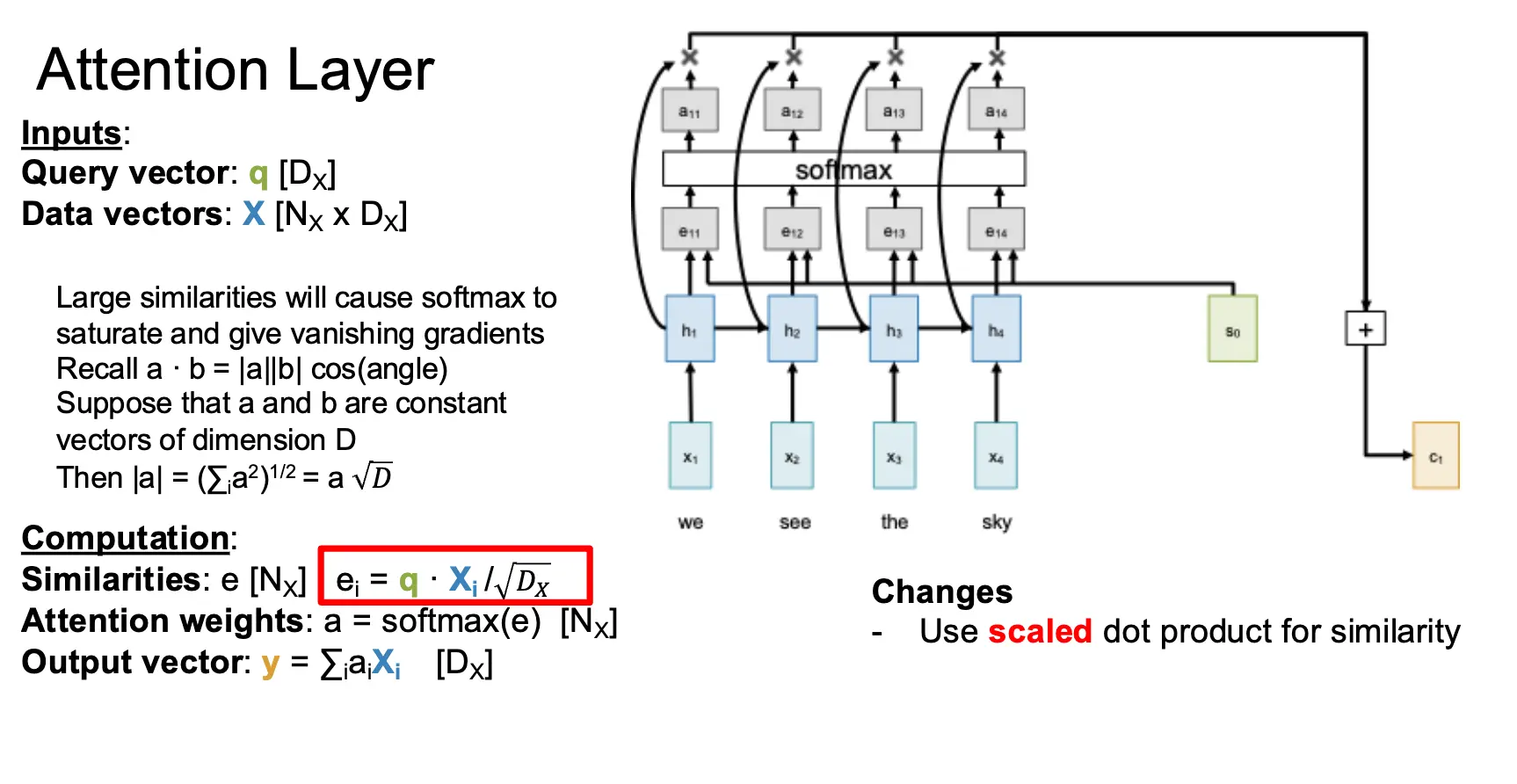
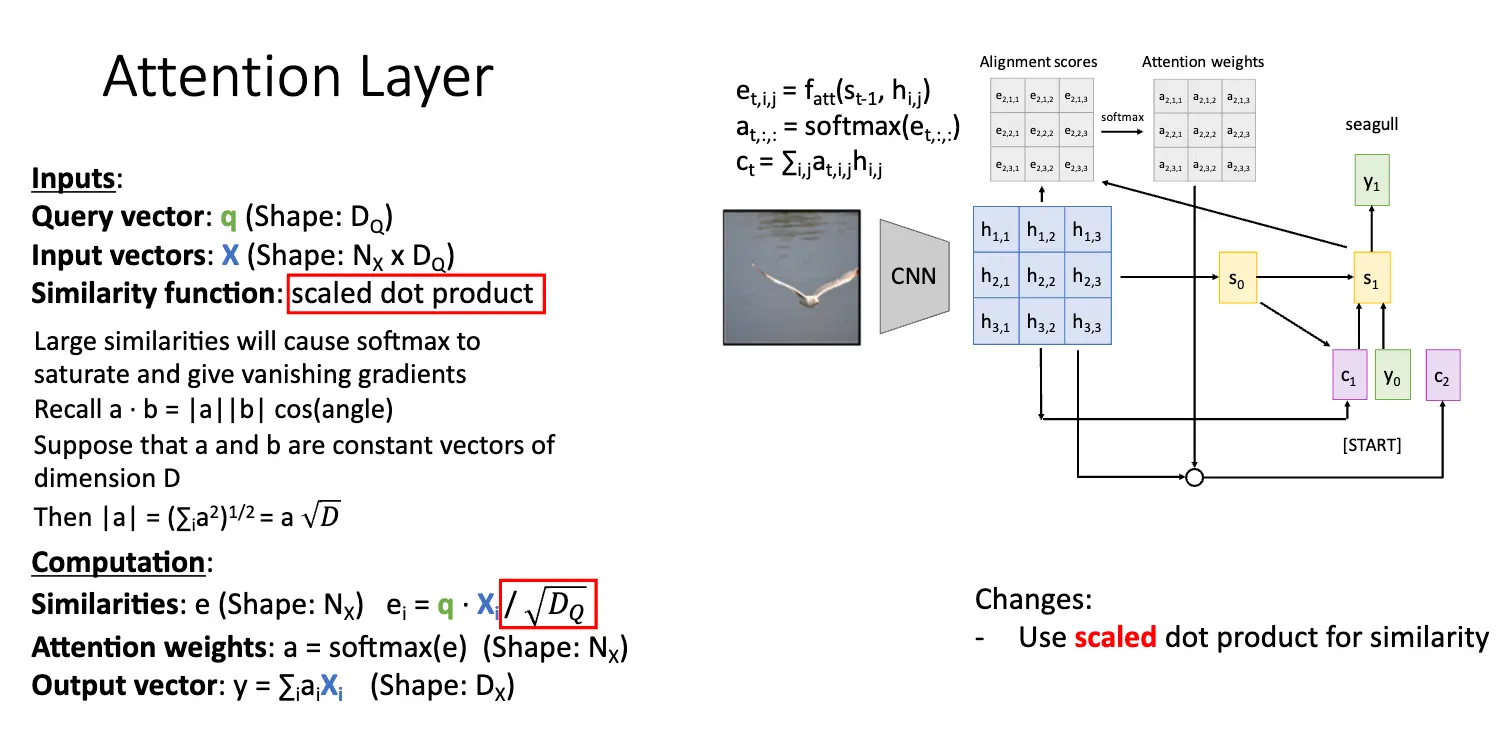
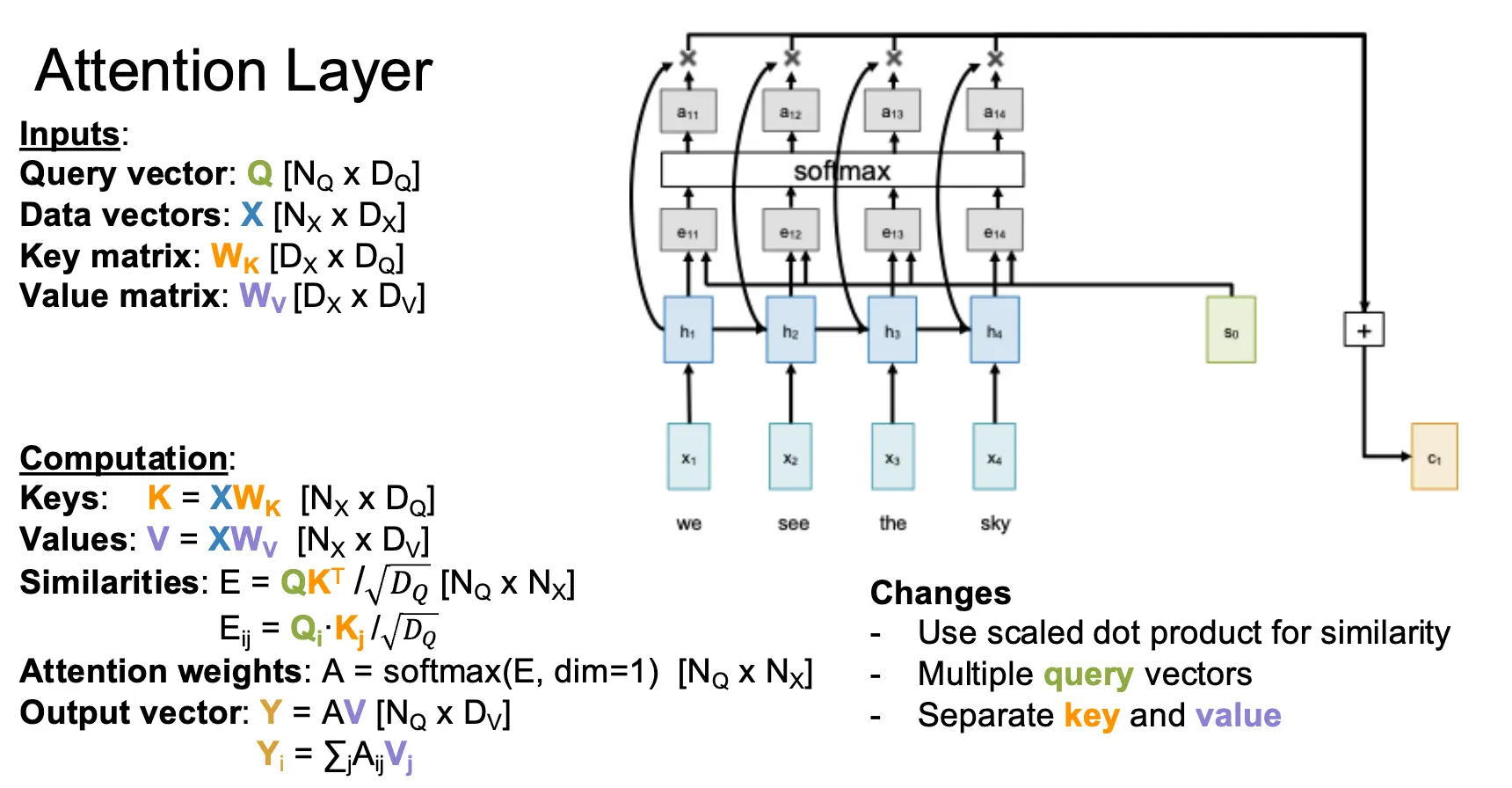
最简单的注意力层的输入是一个查询向量 \(q\)、一个输入序列 \(X\) 和一个相似度函数 \(f_{\text{att}}\)。经过计算得到一个相似度向量 \(e\) 与一个注意力权重 \(a\)，表示查询向量与输入向量序列中每个元素的相似度与重要性，并且产出一个输出向量 \(y\)。需要注意的是，当前相似度函数是点积，点积作为相似度函数已经足够好用了，但是点积和 Softmax 会有奇怪的相互作用，当向量的长度增大的时候，点积的值会增大，而 Softmax 会将这个值压缩，导致梯度消失。因此我们使用缩放点积作为相似度函数，也就是 \(e_i = \dfrac{q \cdot X_i}{\sqrt{D_Q}}\)，其中 \(D_Q\) 是查询向量的维度。

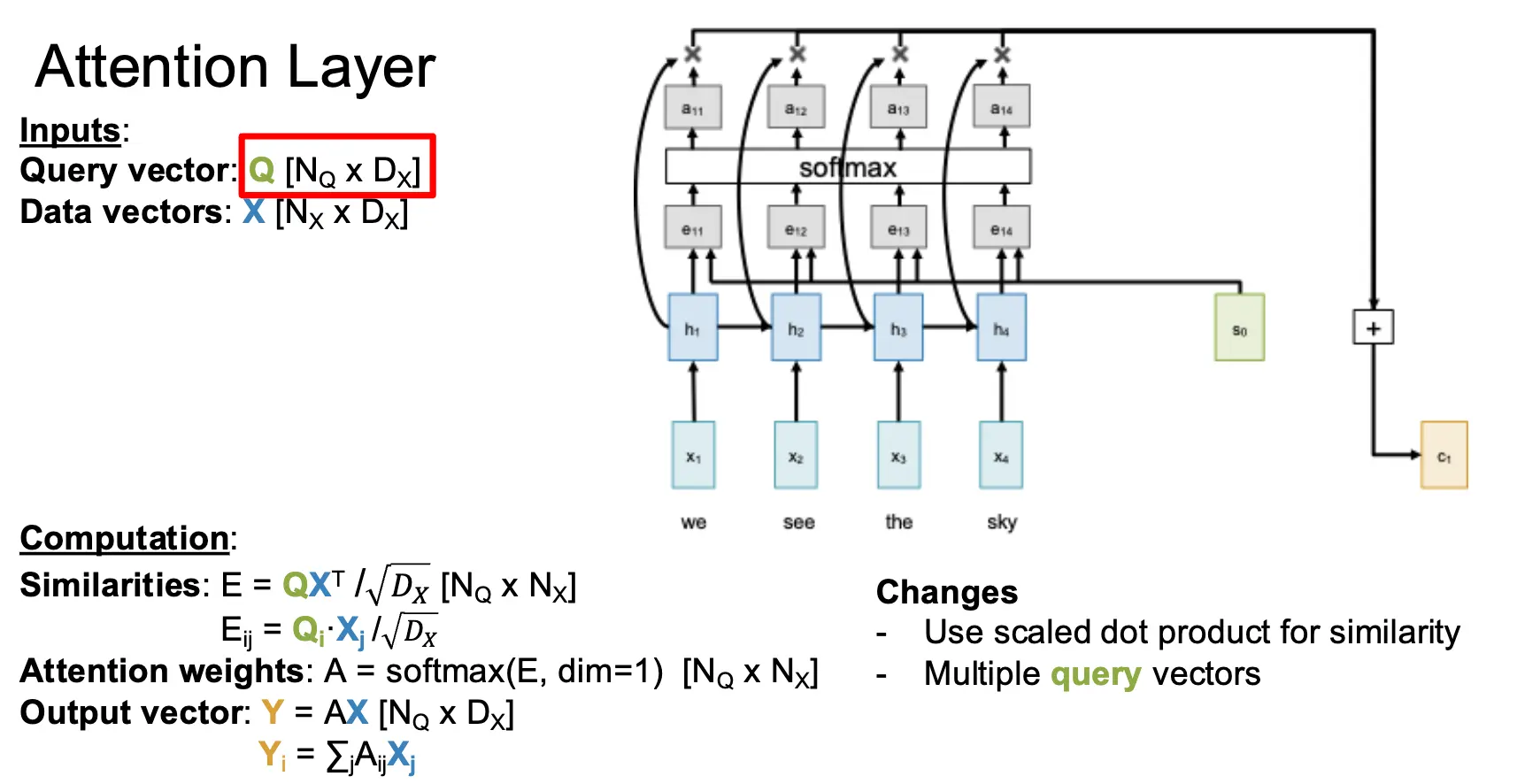
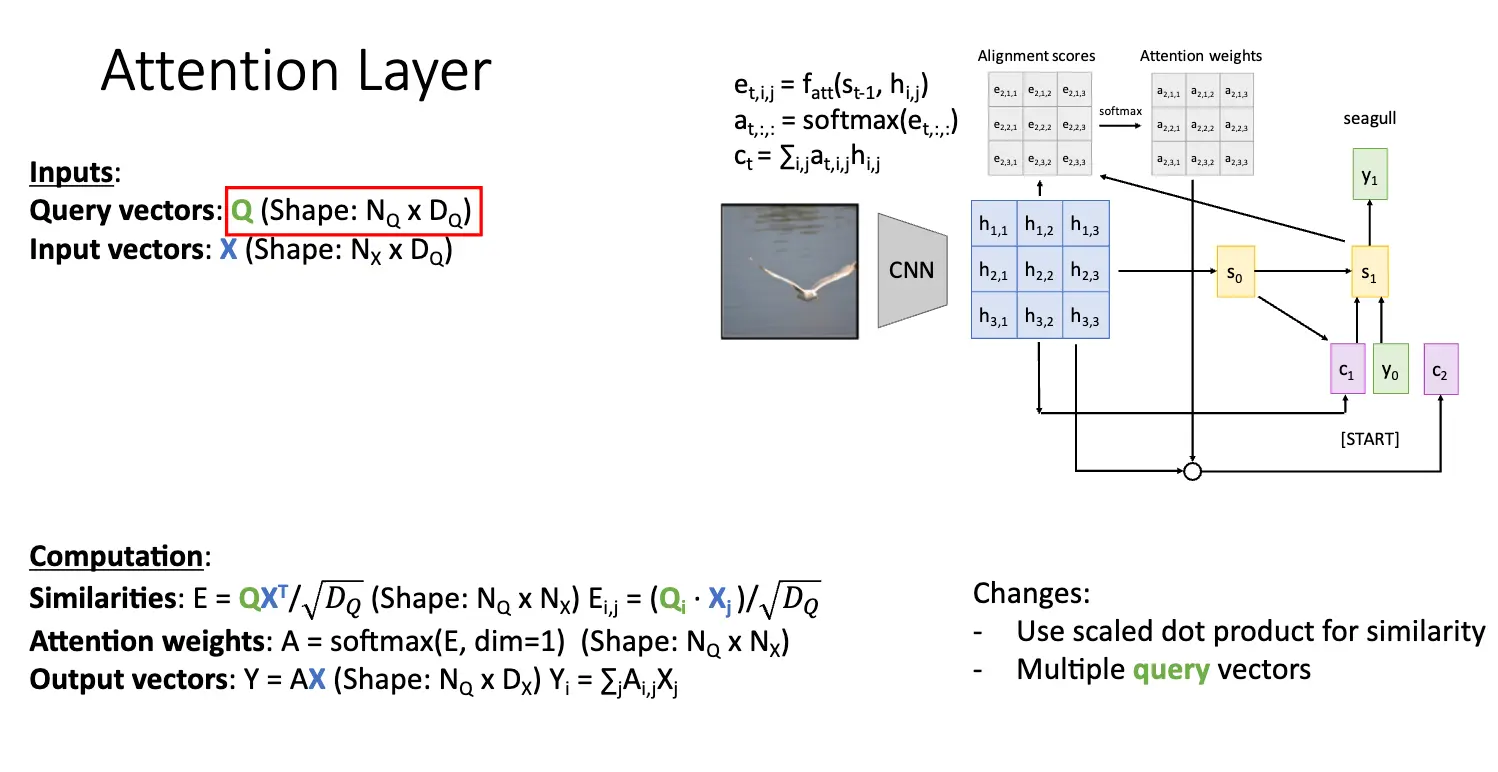
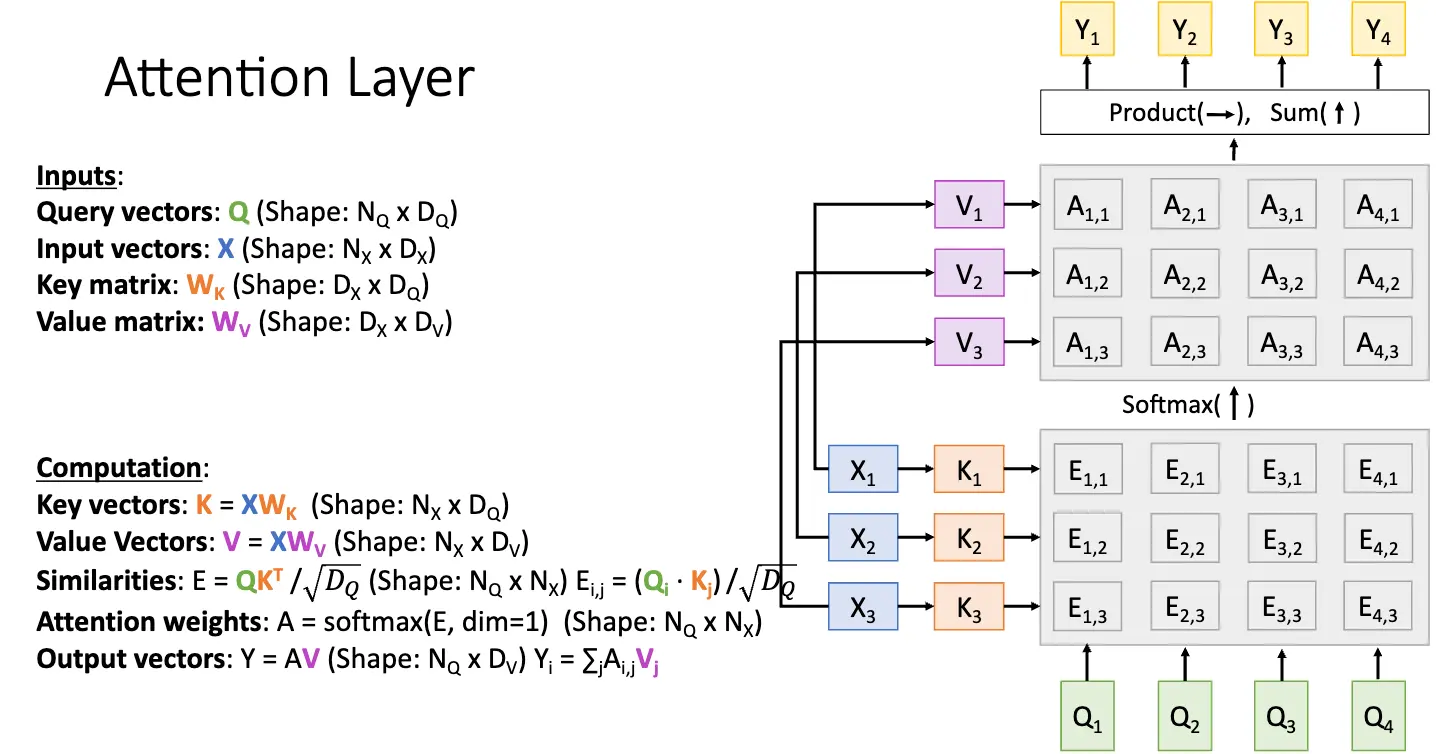
对于多个查询向量 \(Q\)，比如有 \(N_Q\) 个，那么我们就可以计算出每一个查询向量 \(Q_i\) 和每一个输入向量的相似度 \(E_{i, j} = (Q_i \cdot X_j) / \sqrt{D_Q}\)，然后使用 Softmax 函数对相似度矩阵的每一个相似度向量进行归一化，最后计算出输出向量序列。这部分就很直观了。

再进一步泛化，考虑我们使用输入序列 \(X\) 的方式，分在计算相似度的时候被使用，另一部分在计算输出的时候被使用。我们可以将数据向量投射为两个向量：键向量/Key Vector 和值向量/Value Vector，这是通过添加两个可以学习的权重矩阵 \(W_K\) 和 \(W_V\) 实现的。通过将数据向量和权重矩阵相乘，我们就可以得到键向量和值向量。

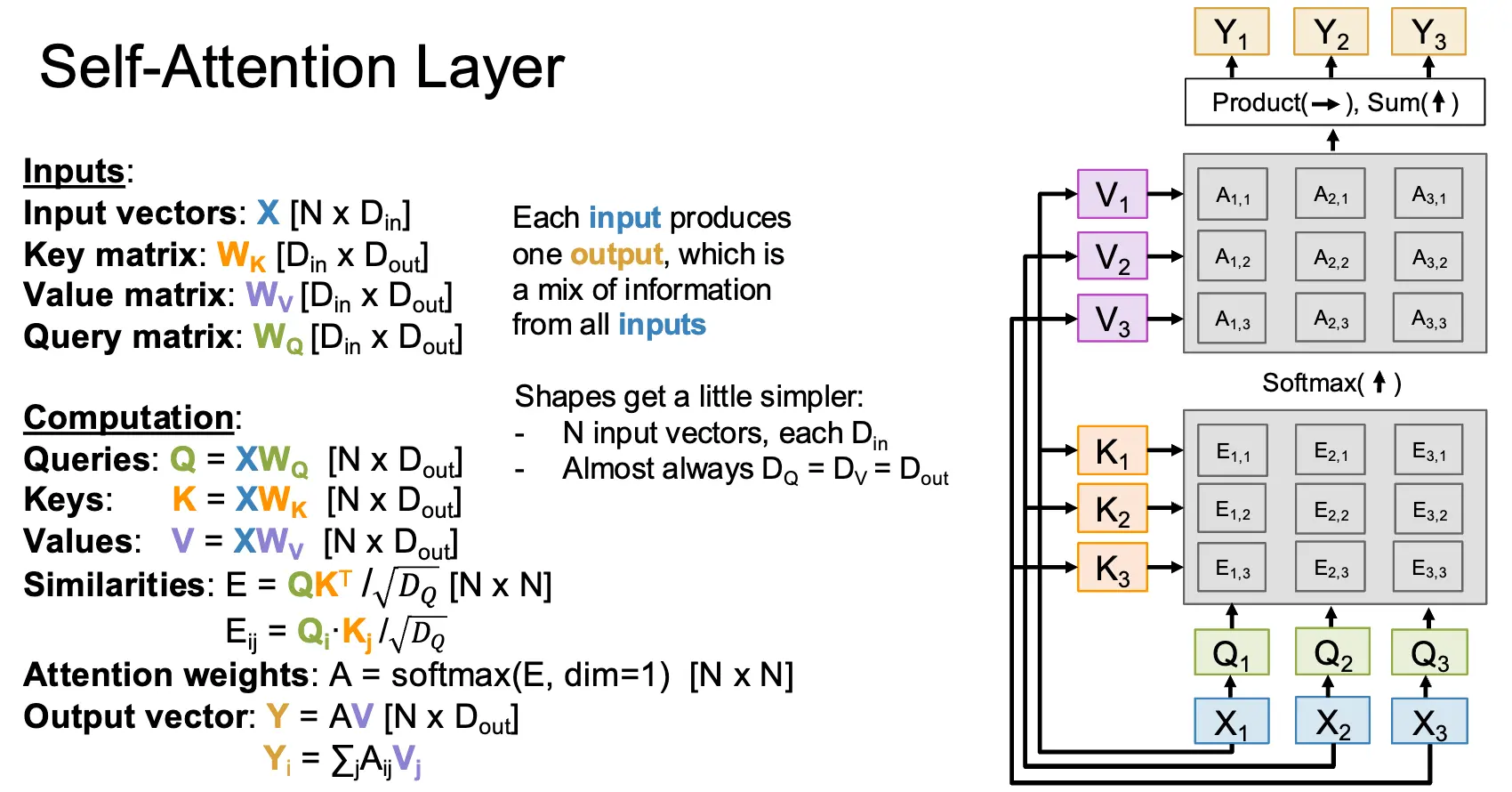
继续进行抽象，我们可以得到自注意力层/Self-Attention Layer：在这里，我们只有一个输入向量，没有输入的查询向量，注意力机制内的查询向量是通过学习一个可学习的查询矩阵 \(W_Q\)，再和输入向量进行矩阵乘得到的。自注意力机制下，这些矩阵的形状都更加简单。在实践上，我们会计算多个矩阵乘法，\([Q \; K \; V] = X[W_Q \; W_K \; W_V]\)，这可以通过一个矩阵乘法实现：\([N \times 3D_{out}] = [N \times D_{in}][D_{in} \times 3D_{out}]\)。因为硬件上少次的大矩阵乘法会比多次的小矩阵乘法更快。

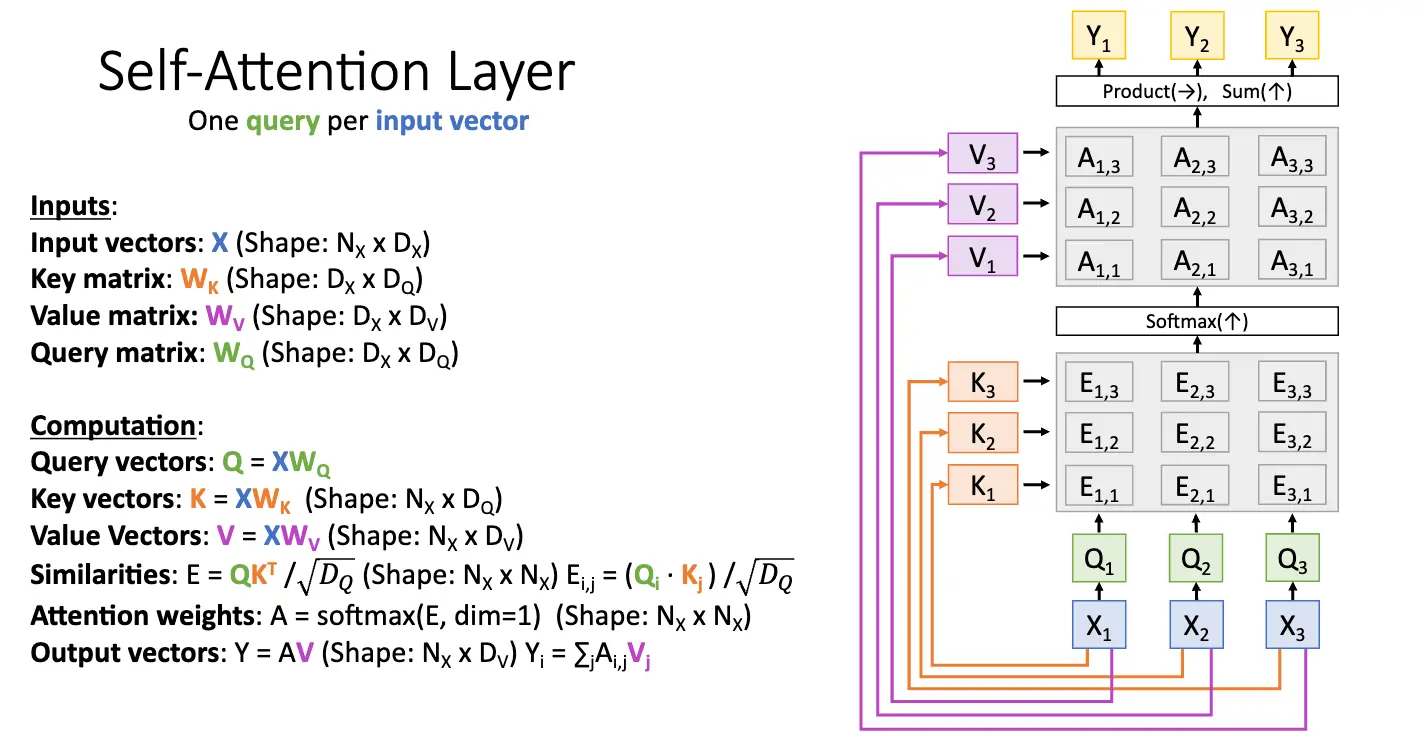
考虑一下，既然我们只有一个输入序列 \(X\)，那么如果我们对输入序列的顺序打乱，那么接下来查询序列和键序列也会被打乱，但是值不变，因此计算出的相似度矩阵和权重矩阵也会被打乱，输出向量序列也会被打乱，因此自注意力层实际上是一个某种意义上的排列不变/Permutation Invariant 的层，我们也叫其排列等价/Permutation Equivariant 的层，满足 \(f(\sigma(x)) = \sigma(f(x))\)，其中 \(\sigma\) 是一个排列函数。这是因为自注意力层根本不指导正在处理的序列的顺序如何，为了让整个处理变得对位置敏感，我们可以添加一些位置编码/Positional Encoding。

有时候我们不希望模型关注到当前时间步之后的位置，也就是不希望提前看到未来的信息，这样有时候相当于作弊，这时候我们可以使用掩码/Mask 来限制模型只能看到当前时间步之前的信息，这样严格限制模型只能使用过去的信息，称为因果掩码/Causal Masking。

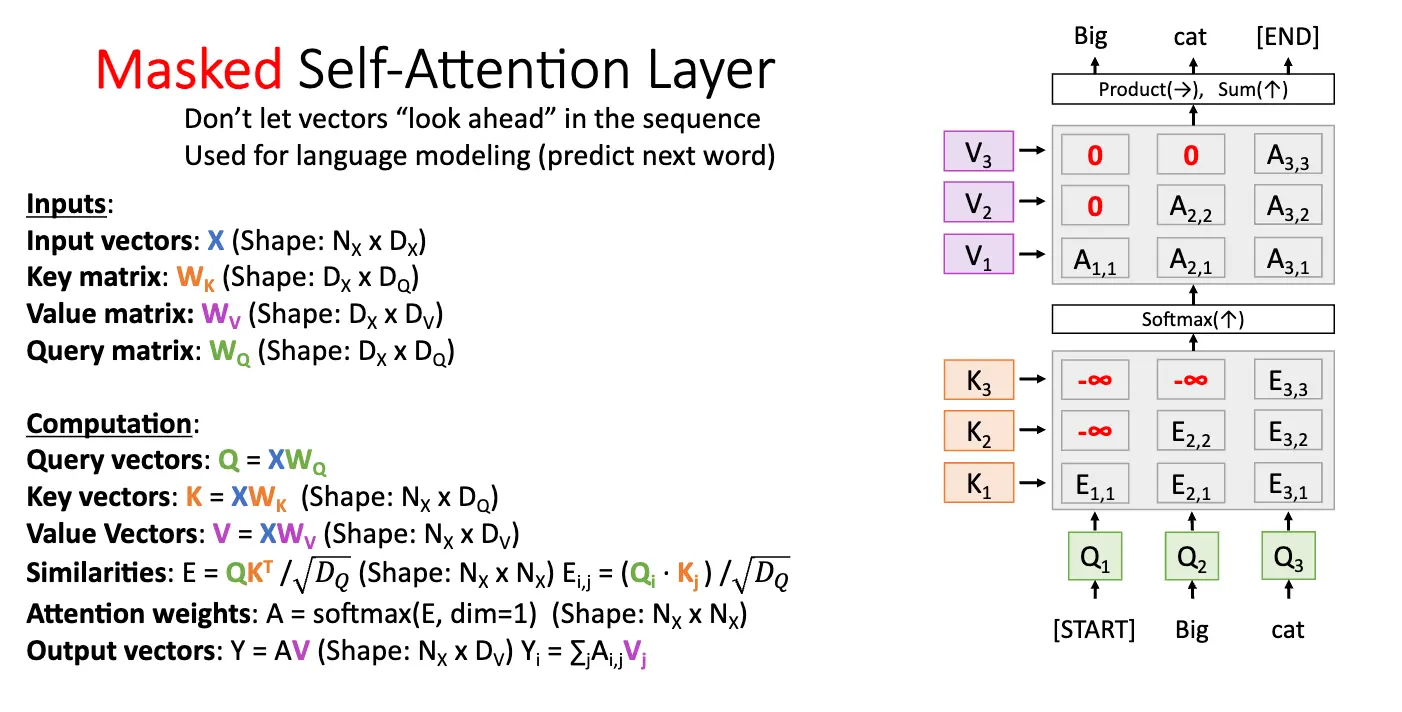
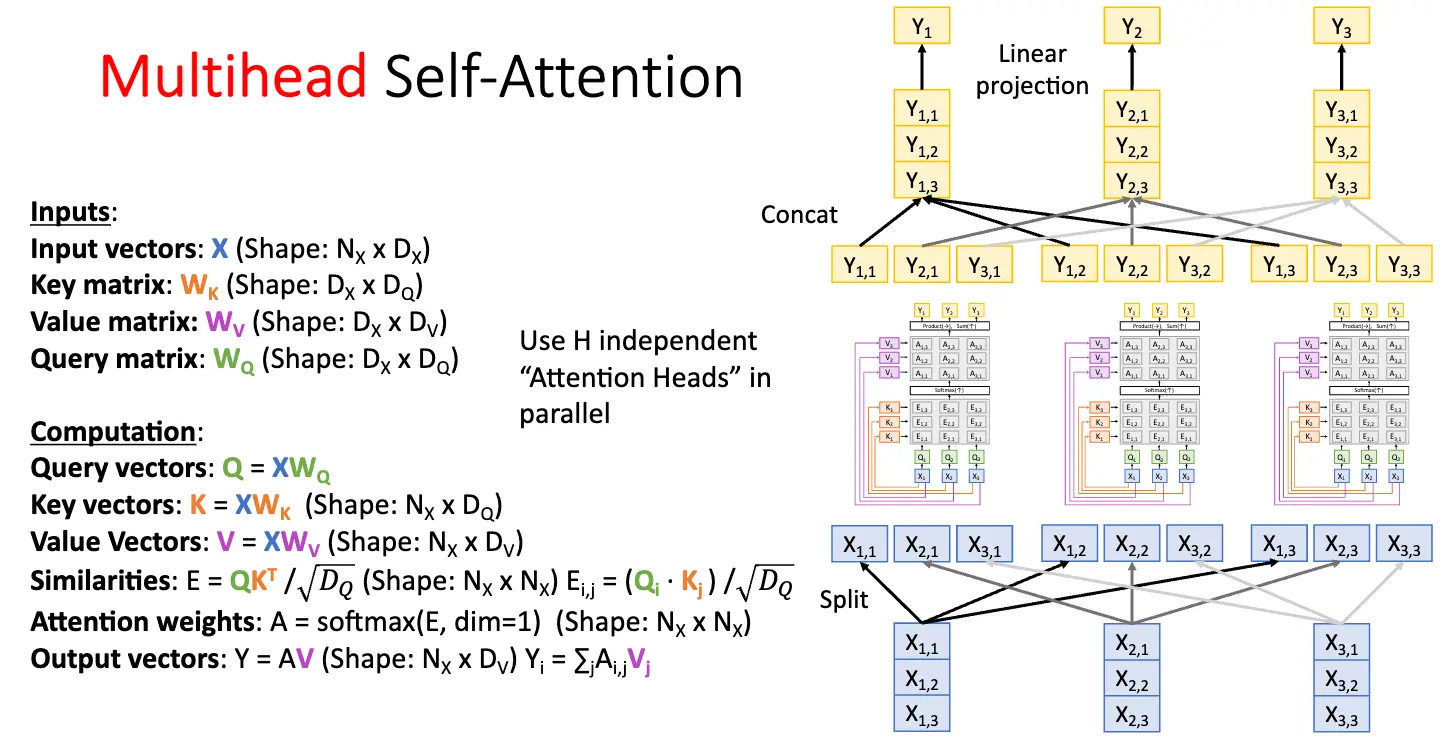
多头注意力层/Multi-Head Attention Layer 通过将输入向量 \(X\) 分成多个头/Head，并对每个头分别计算注意力权重，从而实现对输入序列的多种不同的表示，捕获不同的关系和特征。

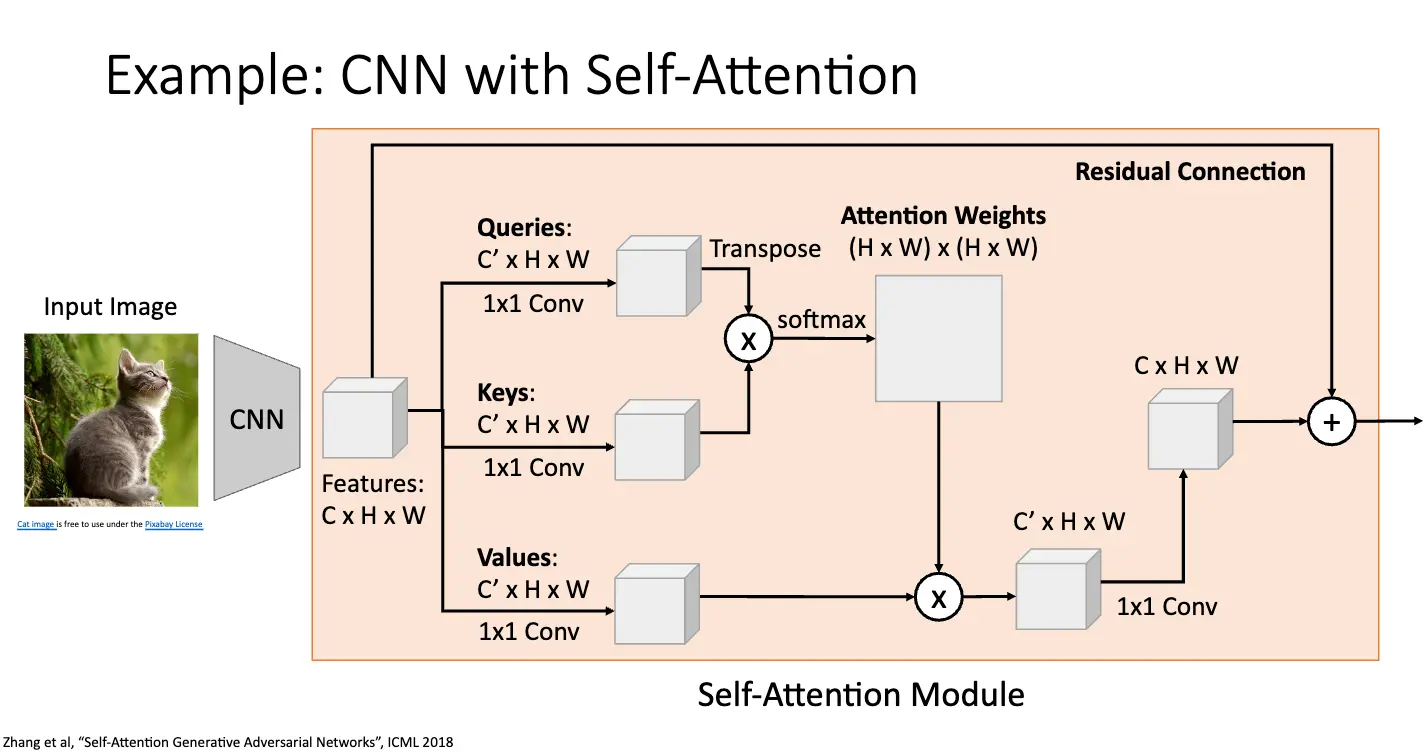
下面就是将 CNN 与自注意力进行结合的例子：

事实上，整个自注意力机制只不过是四次矩阵乘法：

  • QKV 投影：\([N \times D] \times [D \times 3HD_H] \Rightarrow [N \times 3HD_H]\)
  • QK 相似度：\([H \times N \times D_H] \times [H \times D_H \times N] \Rightarrow [H \times N \times N]\)
  • V 加权：\([H \times N \times N] \times [H \times N \times D_H] \Rightarrow [H \times N \times D_H]\)
  • 输出投影：\([N \times HD_H] \times [HD_H \times D] \Rightarrow [N \times D]\)

其对于计算复杂度和内存复杂度都是 \(O(N^2)\)，我们可以使用 Flash Attention 来优化存储，使得内存复杂度降低为 \(O(N)\)。

我们可以基于 Self-Attention 构建出 Transformer 块：假设输入为 \(x_1, x_2, \cdots, x_N\)，首先将输入通过自注意力层，注意自注意力层是整个架构内唯一有向量之间交互的层，然后通过残差连接和层归一化，接着通过多层感知机，最后通过残差连接和层归一化输出为另一个输出向量集合 \(y_1, y_2, \cdots, y_N\)。

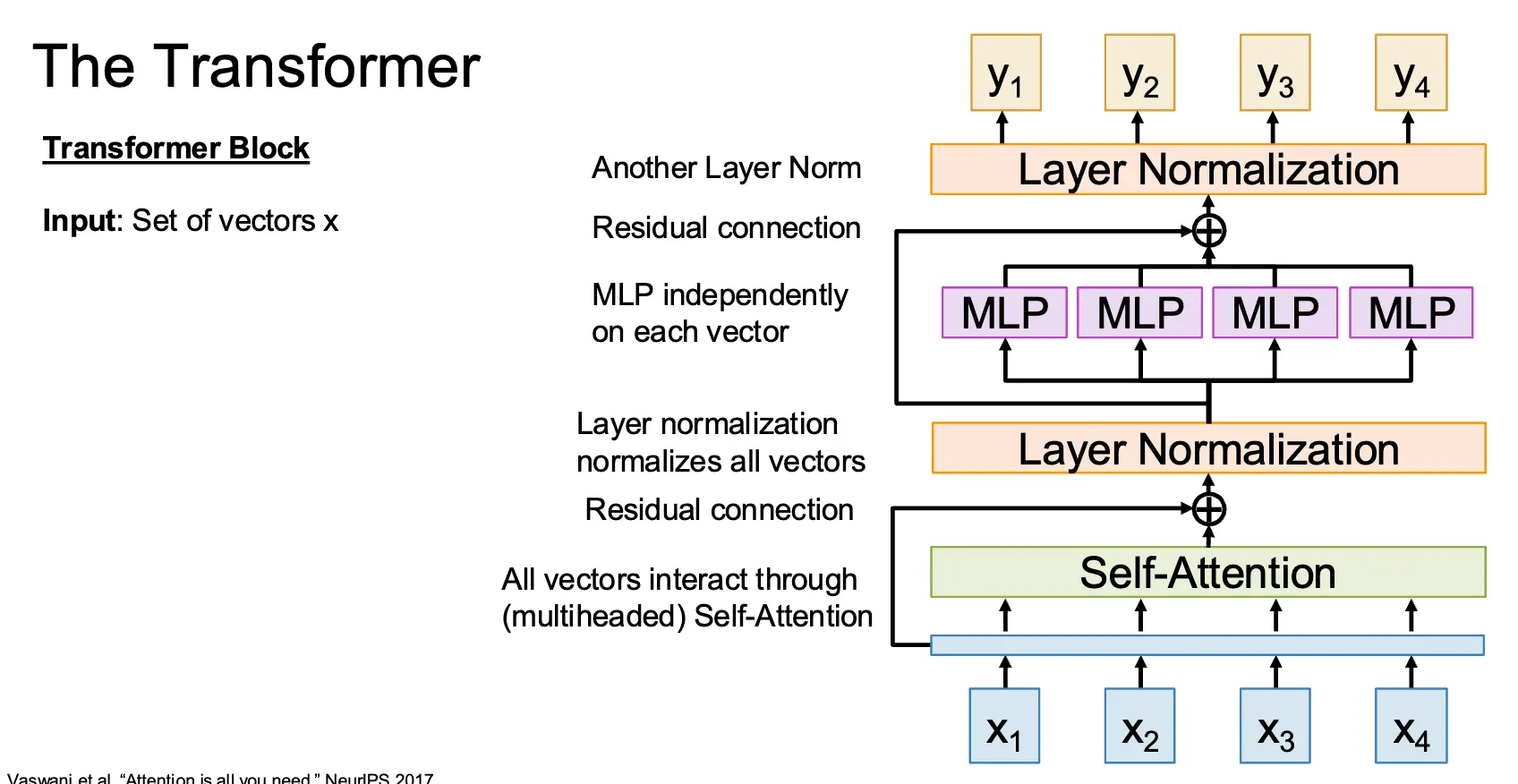
这里面的多层感知机一般是一个两层的神经网络，一般的设置为 \(D \Rightarrow 4D \Rightarrow D\)。层归一化和 MLP 都是分别对每一个输入向量进行操作的。因此一个 Transformer 块的前向传播只需要六次矩阵乘法，四次来自于自注意力层，两次来自于 MLP。且 Transformer 可以高度并行化和扩展化。

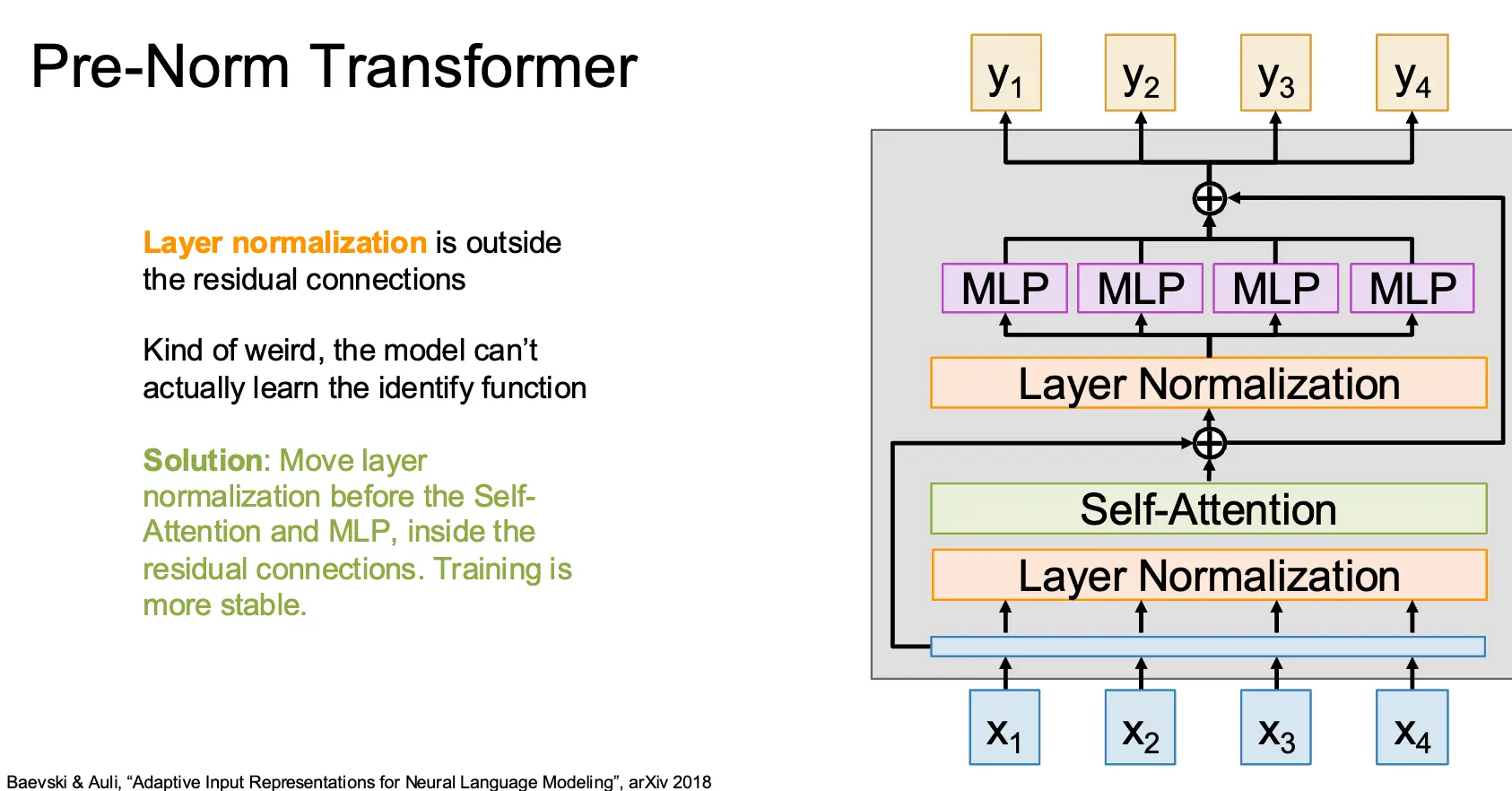
现代的 Transformer 对原来的 Transformer 进行了一些修改，比如将 Layer Normalization 直接放在残差链接外实际上不太好，这样的模型甚至不能学到 Identity Function，因此需要将归一化层放在残差链接内部。

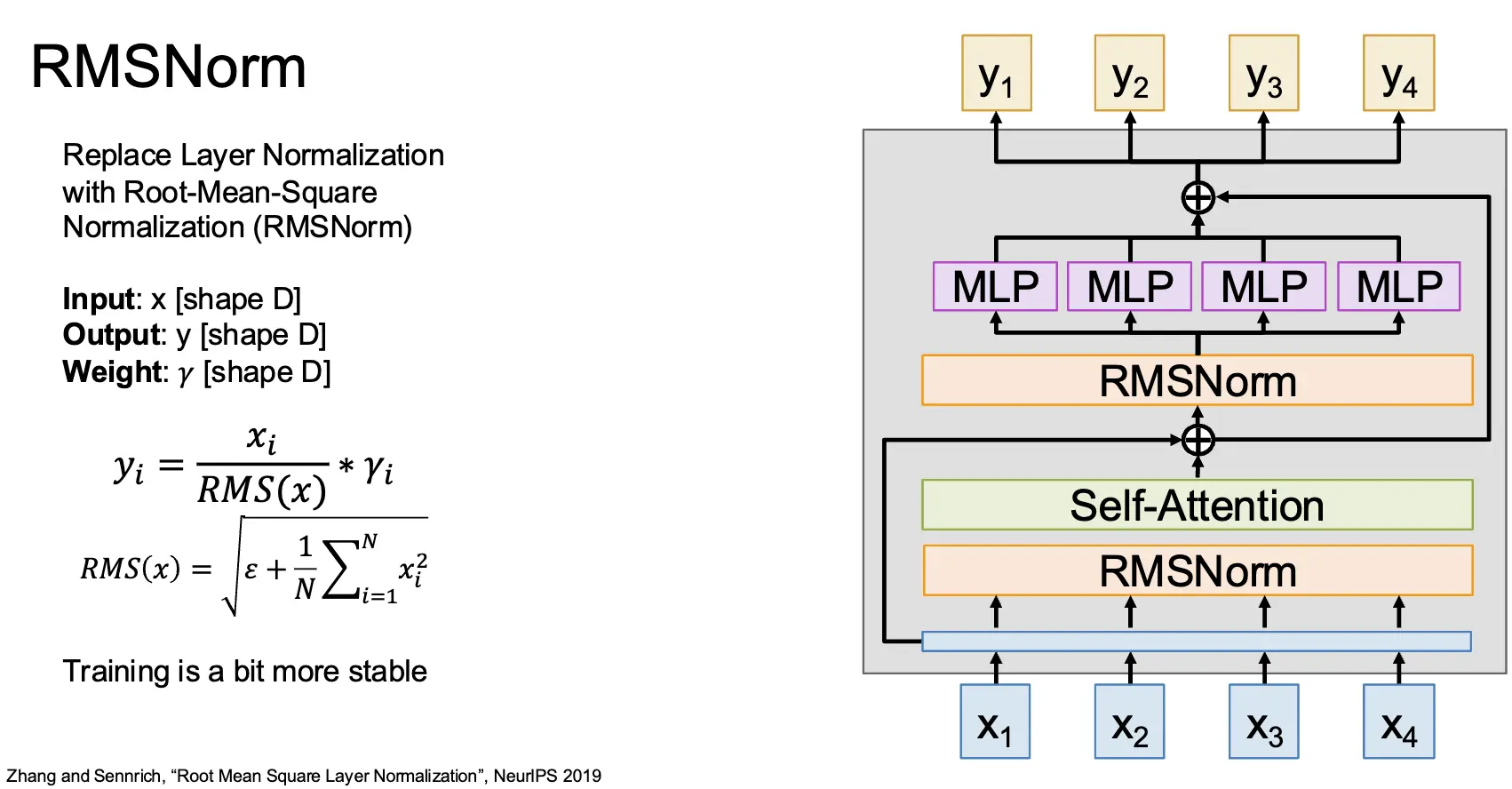
对于归一化来讲，我们还可以使用 RMSNorm/Root-Mean-Square Layer Normalization 来替代 Layer Normalization，其输入为 \(x\)，输出为 \(y\)，权重为 \(\gamma\)，计算为 \(y_i = \frac{x_i}{RMS(x)} * \gamma_i\)，其中 \(RMS(x) = \sqrt{\epsilon + \frac{1}{N}\sum_{i=1}^N x_i^2}\)。这使得训练更加稳定一点。

对于 MLP 来讲，我们还可以使用 SwiGLU MLP 来代替传统的 MLP：SwiGLU MLP 需要学习三个权重矩阵 \(W_1,W_2\)（形状为 \(D \times H\)）和 \(W_3\)（形状为 \(H \times D\)），计算为 \(Y = (\sigma(XW_1) \odot XW_2)W_3\)，其中 \(\odot\) 是逐元素相乘。为了保持总参数量不变，我们设置 \(H = 8D/3\)。

We offer no explanation as to why these architectures seem to work; we attribute their success, as all else, to divine benevolence.

最后，我们还可以使用 MoE 架构：在每个块中学习 \(E\) 个独立的 MLP 权重集；每个 MLP 是一个专家；每个 token 被路由到 \(A < E\) 个活跃专家上，这样总参数增加 \(E\) 倍，但计算只增加 \(A\) 倍。

Lecture 18: Vision Transformers

可以看 别人的笔记