Chapter 7: The Concept of Generalization¶
约 2202 个字 3 张图片 预计阅读时间 7 分钟
7.0 Introduction¶
泛化/Generalization 是机器学习中的核心概念,在强化学习里也没有例外。这里的泛化可以指:
- 在训练数据有限的环境中仍能取得良好性能的能力;
- 在相关环境中迁移并获得良好性能的能力。
在前一种情形里,Agent 必须学会在一个与训练环境完全一致的测试环境中表现良好,这时,泛化的思想与样本效率/Data Efficiency 直接相关,比如当状态-动作空间太大而无法完全覆盖的情况。在后一种情形里,测试环境与训练环境有共同模式,但是环境的动态和奖励可能不同,例如底层动态可能相同,但观测出现了变换,这种变换可能是加入了噪声或者特征偏移等。这种情形与迁移学习/Transfer Learning 以及元学习/Meta Learning 高度相关。
在 Online 设定下,每一步都会做一个 mini-batch 梯度更新,这种情况下,社区有时也把样本效率指代算法的学习速度,这通常在给定步数下学习性能(学习步数就是观察到的转移的数目)。然而,这个结果由许多因素决定:学习算法本身、探索和利用的平衡、以及实际的泛化能力。本章将只注重研究泛化能力,并不考虑学习速度。在我们考虑的设定下,测试环境和训练环境的任务完全相同,我们获得这个任务下一个有限的训练数据集 \(D\)。形式化地,我们定义数据集 \(D\) 为四元组集合 \(\langle s,a,r,s^{\prime} \rangle \in \mathcal{S}\times\mathcal{A}\times\mathcal{R}\times\mathcal{S}\),这些数据是独立同分布采样得到的,记为 \(D \sim \mathcal{D}\),其中 \(\mathcal{D}\) 可以看作训练集数据的分布。采样是按照如下方式:
- 从某个固定的分布下抽取一定数目的状态-动作对 \((s,a)\),满足 \(\mathbb{P}(s,a)>0\),\(\forall (s,a)\in\mathcal{S}\times\mathcal{A}\);
- 下一状态 \(s^{\prime} \sim T(s,a,\cdot)\);
- 回报 \(r = R(s,a,s^{\prime})\)。
记 \(D_\infty\) 为一个四元组数量趋于无穷的极限情形的数据集。
我们可以将一个学习算法看作一个将数据集 \(D\) 映射到策略 \(\pi_D\) 的映射,无论它是否使用模型。此时,期望回报的次优性可以分解为:
这样的分解点明了两个不同的误差来源:
- \(V^{\pi_\ast}(s)-V^{\pi_{D_\infty}}(s)\) 是渐近偏差,和数据量无关;
- \(\mathbb{E}_{D\sim \mathcal{D}} \left[\,V^{\pi_{D_\infty}}(s)-V^{\pi_D}(s)\,\right]\) 是过拟合项,由于样本有限、分布稀疏或有偏,算法可能过拟合到噪声或偶然性上,导致评估/部署性能下降,这一步应该随着数据量增加或者数据质量提高而减小。
从数据集上学到的策略 \(\pi_D\) 的目标是让总体次优性最小。要做到这一点,RL 算法应当与任务/任务集合良好匹配。

如上图所示,提升泛化性能可以看作一种权衡:一方面,完全信任频率学派假设(也就是将有限数据的频率当做概率)带来误差;另一方面,为了降低过拟合而引入的偏差/Bias 也会带来误差/Error,比如引入某种函数逼近结构本身就是强制泛化的一种手段,但可能引入偏差,使用一些正则化技术也是类似的手段。
当数据质量差的时候,算法应该更偏向于更加鲁棒的策略类,也就是更小、更具有泛化力的策略集合;当数据质量提高的时候,过拟合风险降低,算法可以更信任数据,从而降低渐近偏差。这种在渐进偏差和过拟合之间做取舍的权衡,我们称之为偏差-过拟合权衡/Bias-Overfitting Tradeoff。在 Deep RL 中,影响泛化的关键因素有这些:
- 状态表征/State Representation;
- 学习算法/Learning Algorithm,比如 Function Approximator 以及 Model-based 或者 Model-free;
- 目标函数/Objective Function,比如回报塑形/Reward Shaping 和训练时折扣因子调参;
- 分层学习/Hierarchical Learning。
本章内,我们都会使用下面的简单 MDP 进行辅助说明:
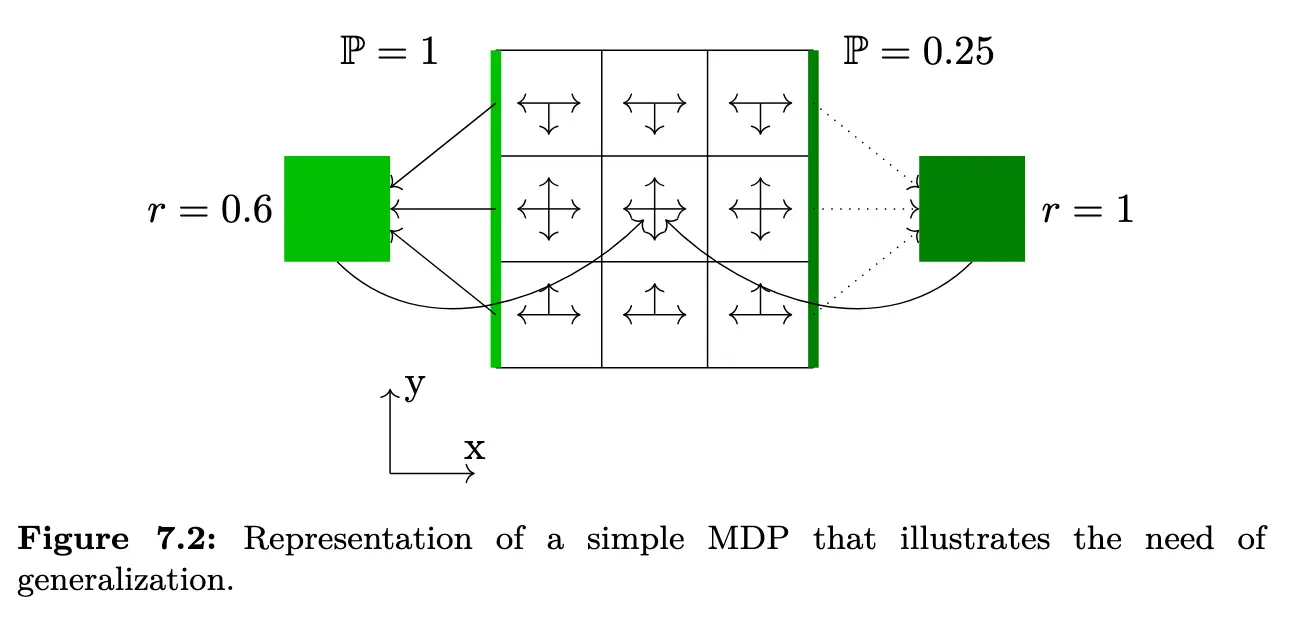
如果 Agent 完全了解环境,其最佳策略就应该是永远向左,每三步获得一次 \(0.6\) 的奖励。现在假设我们只收集到有限的信息,有不小的概率会出现右侧某条转移看起来可以确定性得到 \(r=1\) 的奖励,无论采用基于模型还是无模型的方法,若学习算法在经验 MDP 上找到“最优策略”,它在真实环境上的泛化反而会变差。
7.1 Feature Selection¶
为手头的任务选择合适的特征,是机器学习领域的一个重要话题,在强化学习领域也十分常见,选用恰当级别的抽象在偏差-过拟合权衡之中起着关键的作用,使用小而丰富的表征的一个优势就是可以提升泛化能力。
过拟合:当在很多特征上来决定策略的时候,强化学习算法可能会考虑假相关/Spurious Correlations,从而导致过拟合。比如在 Grid World 的例子中,Agent 很可能会错误的推断 \(y\) 坐标会改变期望回报,进而只选择 \(y\) 坐标来决定策略,这显然是不对的。
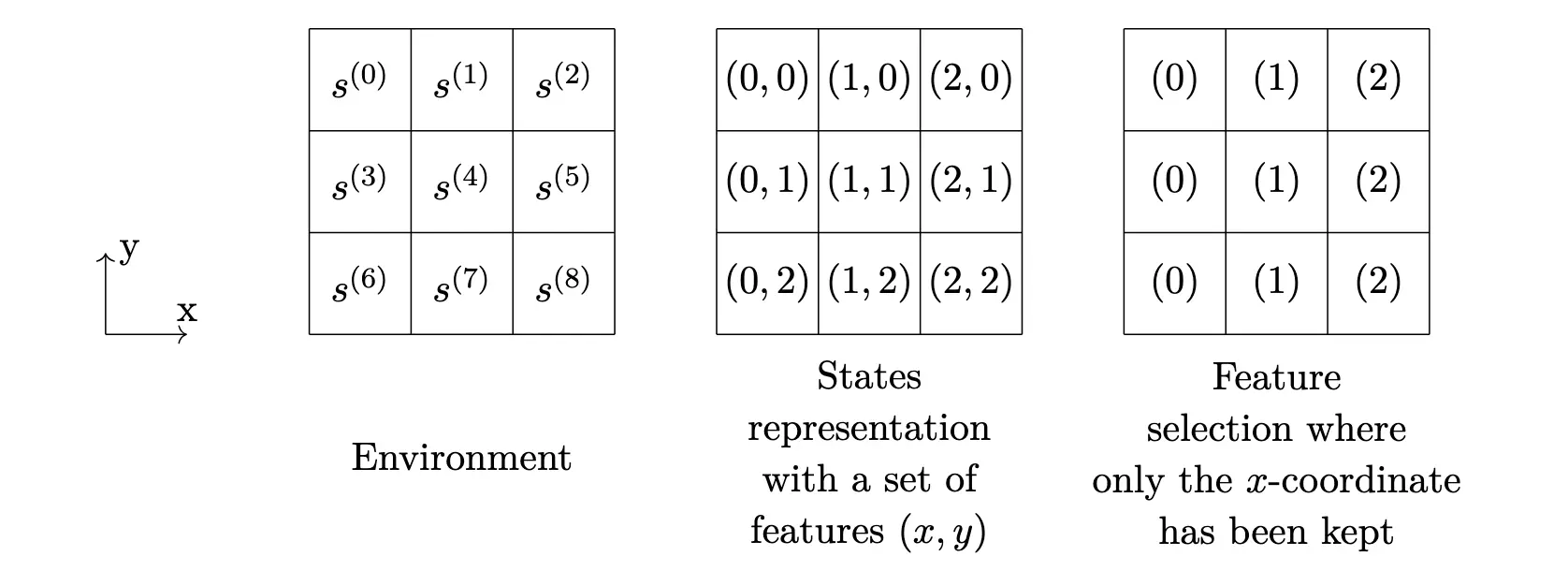
渐进偏差:移除那些在强化学习动态里面扮演区分性角色以区分不同状态的特征,会引入渐进偏差。事实上,无法区分的状态会被强制采用同一策略,因此得到一个次优策略。
在 Deep RL 中,一种方法是先从观测中推断出一组因子化的生成变量/A Factorized Set of Generative Factors。这可以使用编码器-解码器架构的变体。这些特征可以被用作强化学习算法的输入。所学到的表征在某种程度上可以极大有助于泛化,因为其提供了更加简洁/Succinct、更加不易过拟合的表示。
然而,自编码器经常是一种过强的约束,一方面,很多特征可能因为其对重建观测很重要而被保留在抽象表示中,但它们对当前任务其实无关紧要,比如自动驾驶场景中汽车的颜色;另一方面,场景中的关键信息也可能在潜在表示中被丢弃,尤其当该信息 \(x\) 在像素空间中仅占很小比例时。需要注意的是,在深度 RL 设定下,抽象表示与深度学习的使用是交织在一起的。
4) 深度表征学习:自编码器为何“过强”?¶
- 前向/逆向动力学预测:学习能预测 \(s'\) 与 \(r\) 的表示,更对齐“与决策相关”的因素;
- 对比式/时序一致性目标(如 InfoNCE/时序对比):鼓励表征对任务不变因素保持稳定;
- 双模拟度量/状态抽象:直接用“相同的未来回报与转移分布”来约束表示,减少别名化带来的偏差。
5) 实操建议(在离线/有限数据场景尤其有用)¶
- 先小后大:数据少时优先使用更强先验/更小模型/更保守策略类(例如正则更强、值函数/策略网络更浅、行动空间做离散化或选项化)。数据增多再逐步放宽。
-
任务一致的正则:
-
对 \(Q\)/模型加入平滑性与L2/Lipschitz约束,减小对噪声的响应;
- 数据增强(几何、颜色不变形)以压制与任务无关的像素因素;
- 奖励塑形/调低训练折扣因子以减少长视野误差的放大(用轻微偏差换更稳健的估计)。
- 评估要覆盖 OOD:将验证集设计为不同种子/不同观测扰动/轻度动力学变化,专门检查是否“学到了 \(y\) 这样的伪相关”。