Model-free Methods¶
约 685 个字 1 张图片 预计阅读时间 2 分钟
Lecture 5: Policy Gradients¶
有关重要性采样的方法可以参考 Levine & Koltun (2013) 这篇论文。
策略梯度法还有哪些问题?如果从梯度下降方法的角度上看,我们考虑下面这个问题:下面这个环境设定下,reward 不仅和当前状态相关,还对动作添加了一个惩罚项,策略可以看作一个高斯策略。
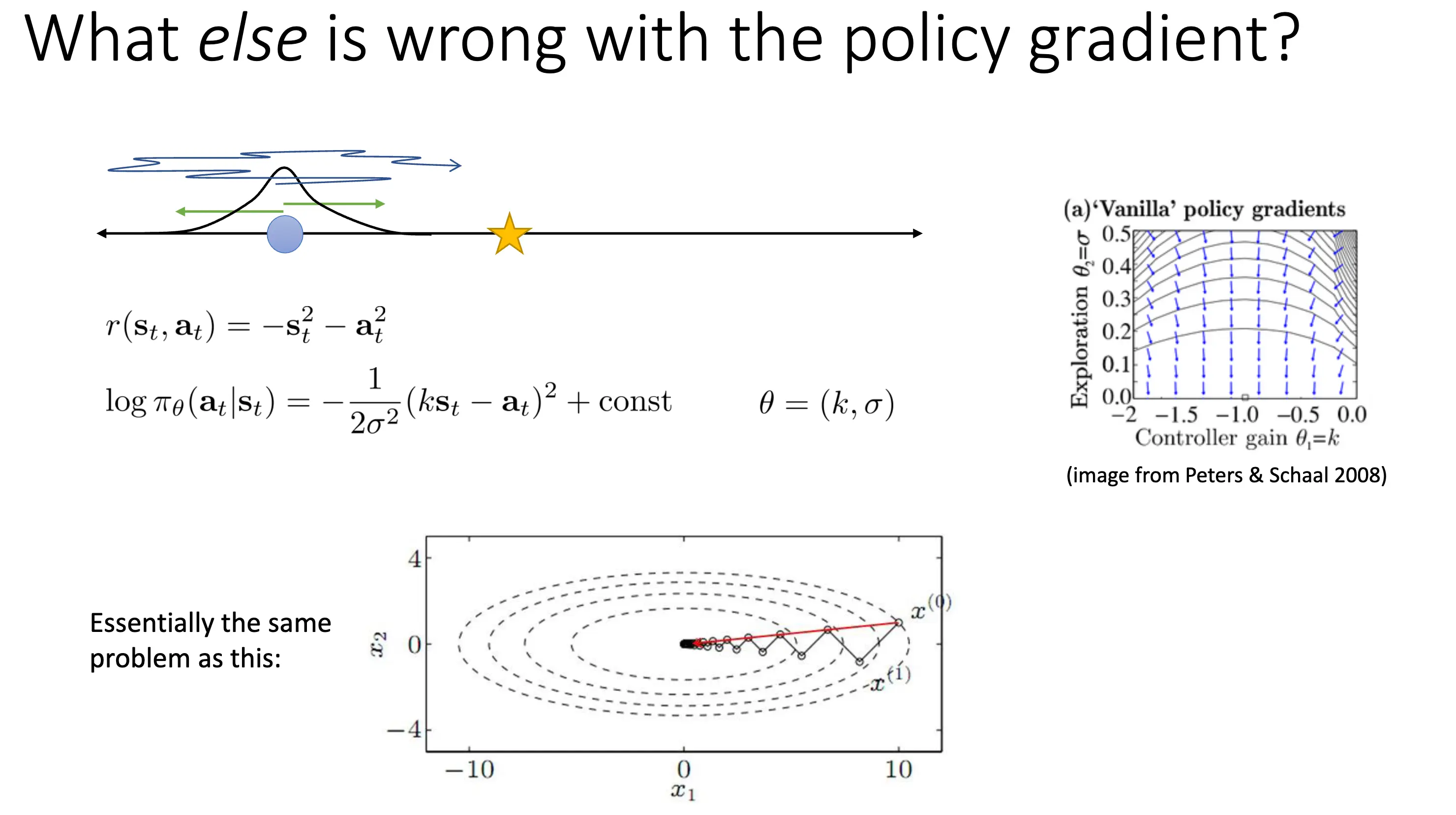
最优解应该在 \(\sigma = 0\),\(k = -1\) 处。从右面梯度图示可以看出,梯度方向事实上没有严格指向最优点,这是因为随着 \(\sigma\) 变小,关于 \(\sigma\) 的梯度量级急剧变大,而关于 \(k\) 的梯度相对来说很小,结果是更新几乎被挤压到减小 \(\sigma\) 上,向最优 \(k\) 的推进变得极慢。这种问题在优化上是 ill-conditioned 的,就好像优化一个特征值极大的二次函数一样困难。接下来介绍可以缓解这个问题的 Covariant/Natural Policy Gradient 方法。
在 Deep RL 下,我们的策略是一个神经网络,很可能有某些参数对策略的影响量级差别巨大,直觉上应当对影响策略小的参数用更大的步,对影响策略大的参数用更小的步。我们也可以使用约束优化的角度来看这个问题,优化目标是 \(J(\theta)\) 的泰勒展开:
可以看作要求 \(\theta'\) 在 \(\theta\) 的 \(\varepsilon\) 邻域内,找到最大化目标线性更新的参数值。但是直接在参数空间下进行约束比较困难,可以在策略空间下参数化这个过程。
这里的 \(D\) 是一个和参数化无关的散度度量,比较常见的是 KL 散度:\(D_{\text{KL}}(\pi_{\theta'} \| \pi_\theta) = \mathbb{E}_{\pi_{\theta'}} [\log \pi_{\theta} - \log \pi_{\theta'}] \approx (\theta' - \theta)^T \mathbf{F} (\theta' - \theta)\),\(F(\theta)\) 是 Fisher Information Matrix,其值为 \(\mathbf{F} = \mathbb{E}_{\pi_\theta} [\nabla_\theta \log \pi_\theta (a \mid s) \nabla_\theta \log \pi_\theta (a \mid s)^T]\)。于是优化问题可以转化为:
这就是我们的 Covariant/Natural Policy Gradient 方法,其可以很好缓解我们之前情景下的问题。比如 TRPO 的现代方法很多都收到自然策略梯度的启发,使用共轭梯度下降等优化手法。