跳转至

Chapter 9: 聚类

约 4053 个字 6 张图片 预计阅读时间 14 分钟

1. 聚类任务

在无监督学习中，训练样本的标记信息是未知的，目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律，此类任务中研究最多、应用最广的是聚类/Clustering。聚类的目标是将数据集中的样本划分为若干个通常是不相交的子集，每个子集称为一个簇/Cluster。通过这样的划分，每个簇可能对应于一些潜在的概念。

形式化地说，假定样本集 \(D = \{\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_m\}\) 包含 \(m\) 个无标记样本，每个样本 \(\boldsymbol{x}_i = (x_{i1}; x_{i2}; \ldots; x_{in})\) 是一个 \(n\) 维特征向量，则聚类算法将样本集 \(D\) 划分为 \(k\) 个不相交的簇 \(\{C_l \mid l=1,2,\ldots,k\}\)，其中 \(C_{l^{\prime}} \bigcap_{l \neq l^{\prime}} C_l = \varnothing\) 且 \(D = \bigcup_{l=1}^k C_l\)。相应地，我们用 \(\lambda_j \in \{1,2,\ldots,k\}\) 表示样本 \(\boldsymbol{x}_j\) 的簇标记/Cluster Label，即 \(\boldsymbol{x}_j \in C_{\lambda_j}\)。于是，聚类的结果可用包含 \(m\) 个元素的簇标记向量 \(\lambda = (\lambda_1, \lambda_2, \ldots, \lambda_m)\) 表示。

2. 性能度量

聚类性能度量也被称为聚类有效性指标/Vailidity Index。与监督学习中的性能度量作用相似，对聚类结果，我们需通过某种性能度量来评估其好坏；另一方面，若明确了最终要使用的性能度量，则可直接将其作为聚类过程的优化目标，从而更好地得到符合要求的聚类结果。我们希望聚类的簇内相似度/Intra-cluster Similarity 高且簇间相似度/Inter-cluster Similarity 低。

聚类性能度量大致有两类。一类是将聚类结果与某个参考模型/Reference Model 进行比较，称为外部指标/External Index；另一类是直接考察聚类结果而不用任何参考模型，称为内部指标/Internal Index。

对于数据集 \(D = \{\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_m\}\)，假定通过聚类给出的簇划分为 \(\mathcal{C} = \{C_1, C_2, \ldots, C_k\}\)，参考模型给出的簇划分为 \(\mathcal{C}^* = \{C_1^*, C_2^*, \ldots, C_k^*\}\)。相应地，令 \(\lambda\) 与 \(\lambda^*\) 分别表示与 \(\mathcal{C}\) 和 \(\mathcal{C}^*\) 对应的簇标记向量。我们将样本两两配对考虑，定义

\[\begin{aligned} a &= |SS|, \enspace SS = \{(\boldsymbol{x}_i, \boldsymbol{x}_j) \mid \lambda_i = \lambda_j, \lambda_i^* = \lambda_j^*, i < j\}, \\ b &= |SD|, \enspace SD = \{(\boldsymbol{x}_i, \boldsymbol{x}_j) \mid \lambda_i = \lambda_j, \lambda_i^* \neq \lambda_j^*, i < j\}, \\ c &= |DS|, \enspace DS = \{(\boldsymbol{x}_i, \boldsymbol{x}_j) \mid \lambda_i \neq \lambda_j, \lambda_i^* = \lambda_j^*, i < j\}, \\ d &= |DD|, \enspace DD = \{(\boldsymbol{x}_i, \boldsymbol{x}_j) \mid \lambda_i \neq \lambda_j, \lambda_i^* \neq \lambda_j^*, i < j\}, \end{aligned}\]

由于每一个样本对都只能出现在一个集合中，因此有 \(a + b + c + d = m(m-1)/2\) 成立。基于上述定义，可导出一些常用的聚类性能度量外部指标：

  • Jaccard 系数/Jaccard Coefficient/JC：

    \[\text{JC} = \frac{a}{a + b + c}.\]

  • FM 指数/Fowlkes and Mallows Index/FMI：

    \[\text{FMI} = \sqrt{\frac{a}{a + b} \cdot \frac{a}{a + c}}.\]

  • Rand 指数/Rand Index/RI：

    \[\text{RI} = \frac{2(a + d)}{m(m-1)}.\]

显然，上述性能度量的结果值均在 \([0,1]\) 区间，值越大越好。

考虑聚类结果的簇划分 \(\mathcal{C} = \{C_1, C_2, \ldots, C_k\}\)，定义

\[\begin{aligned} \text{avg}(C) &= \frac{2}{|C|(|C|-1)} \sum_{1 \leq i < j \leq |C|} \text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_j), \\ \text{diam}(C) &= \max_{1 \leq i < j \leq |C|} \text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_j), \\ d_{\min}(C_i, C_j) &= \min_{\boldsymbol{x} \in C_i, \boldsymbol{x}^{\prime} \in C_j} \text{dist}(\boldsymbol{x}, \boldsymbol{x}^{\prime}), \\ d_{\text{cen}}(C_i, C_j) &= \text{dist}(\boldsymbol{\mu}_i, \boldsymbol{\mu}_j), \end{aligned}\]

其中，\(\text{dist}(\cdot, \cdot)\) 用于计算两个样本之间的距离；\(\boldsymbol{\mu}\) 代表簇 \(C\) 的中心点 \(\boldsymbol{\mu} = \frac{1}{|C|}\sum_{\boldsymbol{x} \in C} \boldsymbol{x}\)。显然，\(\text{avg}(C)\) 对应于簇 \(C\) 内样本间的平均距离，\(\text{diam}(C)\) 对应于簇 \(C\) 内样本间的最远距离，\(d_{\min}(C_i, C_j)\) 对应于簇 \(C_i\) 与簇 \(C_j\)最近样本间的距离，\(d_{\text{cen}}(C_i, C_j)\) 对应于簇 \(C_i\) 与簇 \(C_j\) 中心点间的距离。基于上述定义，可导出一些常用的聚类性能度量内部指标：

  • DB 指数/Davies-Bouldin Index/DBI：

    \[\text{DBI} = \frac{1}{k} \sum_{i=1}^k \max_{j \neq i} \left( \frac{\text{avg}(C_i) + \text{avg}(C_j)}{d_{\text{cen}}(\boldsymbol{\mu}_i, \boldsymbol{\mu}_j)} \right).\]

  • Dunn 指数/Dunn Index/DI：

    \[\text{DI} = \min_{1 \leq i \leq k} \left\{ \min_{j \neq i} \left\{ \frac{d_{\min}(C_i, C_j)}{\max_{1 \leq l \leq k} \text{diam}(C_l)} \right\} \right\}.\]

显然，\(\text{DBI}\) 的值越小越好，而 \(\text{DI}\) 则相反，值越大越好。

3. 距离计算

对函数 \(\text{dist}(\cdot, \cdot)\)，若它是一个距离度量/Distance Measure，则需满足一些基本性质：

  • 非负性/Non-negativity：\(\text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_j) \geq 0;\)
  • 同一性/Identity：\(\text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_j) = 0 \Leftrightarrow \boldsymbol{x}_i = \boldsymbol{x}_j;\)
  • 对称性/Symmetry：\(\text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_j) = \text{dist}(\boldsymbol{x}_j, \boldsymbol{x}_i);\)
  • 直递性/Triangle Inequality：\(\text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_j) \leq \text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_k) + \text{dist}(\boldsymbol{x}_k, \boldsymbol{x}_j).\)

给定样本 \(\boldsymbol{x}_i = (x_{i1}; x_{i2}; \ldots; x_{in})\) 与 \(\boldsymbol{x}_j = (x_{j1}; x_{j2}; \ldots; x_{jn})\)，最常用的是闵可夫斯基距离/Minkowski Distance：

\[\text{dist}_{\text{mk}}(\boldsymbol{x}_i, \boldsymbol{x}_j) = \left( \sum_{u=1}^n |x_{iu} - x_{ju}|^p \right)^{\frac{1}{p}} = \lVert \boldsymbol{x}_i - \boldsymbol{x}_j \rVert_p.\]

闵可夫斯基距离显然满足度量的四条性质，同时其对 \(p\) 单调递增。

  • 当 \(p = 2\) 时，闵可夫斯基距离即欧氏距离/Euclidean Distance：

    \[\text{dist}_{\text{ed}}(\boldsymbol{x}_i, \boldsymbol{x}_j) = \lVert \boldsymbol{x}_i - \boldsymbol{x}_j \rVert_2 = \sqrt{\sum_{u=1}^n |x_{iu} - x_{ju}|^2}.\]

  • 当 \(p = 1\) 时，闵可夫斯基距离即曼哈顿距离/Manhattan Distance：

    \[\text{dist}_{\text{man}}(\boldsymbol{x}_i, \boldsymbol{x}_j) = \lVert \boldsymbol{x}_i - \boldsymbol{x}_j \rVert_1 = \sum_{u=1}^n |x_{iu} - x_{ju}|.\]

我们通常是基于某种形式的距离来定义相似度度量/Similarity Measure，距离越大，相似度越小。然而，用于相似度度量的距离未必需要满足距离度量的所有基本性质，尤其是三角不等式。例如在某些任务中我们可能会定义这样的相似度度量：人和猿相似，人和人马相似，但是人马和猿不相似。这样的不满足三角不等式的距离称为非度量距离/Non-metric Distance。

本节中的距离计算式都是事先定义好的，但在不少现实任务中我们可能难以确定合适的距离计算式，这可通过距离度量学习/Distance Metric Learning 来实现。

我们将属性分为连续属性/Continuous Attribute 和离散属性/Categorical Attribute；有序属性/Ordinal Attribute 和无序属性/Non-ordinal Attribute。连续属性也称为数值属性/Numerical Attribute，离散属性也称为列名属性/Nominal Attribute。

在讨论距离的计算时，属性是否定义了序关系更加重要一些，例如定义域为 \(\{1,2,3\}\) 的离散属性与连续属性的性质更接近一些，能直接在属性值上计算距离。闵可夫斯基距离可以用于有序属性，对于无序属性，我们可以定义 VDM 距离/Value Difference Metric：

\[\text{VDM}_p(a, b) = \sum_{i=1}^k \left| \frac{m_{u,a,i}}{m_{u,a}} - \frac{m_{u,b,i}}{m_{u,b}} \right|^p.\]

其中，\(m_{u,a}\) 表示在属性 \(u\) 上取值为 \(a\) 的样本数，\(m_{u,a,i}\) 表示在第 \(i\) 个样本簇中在属性 \(u\) 上取值为 \(a\) 的样本数，\(k\) 为样本簇数。将闵可夫斯基距离和 VDM 结合即可处理混合属性，首先假定有 \(n_c\) 个有序属性和 \(n-n_c\) 个无序属性，不失一般性，令有序属性排列在无序属性之前：

\[\text{MinkovDM}_p(\boldsymbol{x}_i, \boldsymbol{x}_j) = \left( \sum_{u=1}^{n_c} |x_{iu} - x_{ju}|^p + \sum_{u=n_c+1}^n \text{VDM}_p(x_{iu}, x_{ju}) \right)^{\frac{1}{p}}.\]

当样本空间中不同属性的重要性不同时，可使用加权距离/Weighted Distance：

\[\text{dist}_{\text{wmk}}(\boldsymbol{x}_i, \boldsymbol{x}_j) = \left( w_1 \cdot |x_{i1} - x_{j1}|^p + \ldots + w_n \cdot |x_{in} - x_{jn}|^p \right)^{\frac{1}{p}},\]

其中，权重 \(w_i \geq 0\) 表征不同属性的重要性，通常 \(\sum_{i=1}^n w_i = 1\)。

4. 原型聚类

原型/Prototype 是指样本空间中的具有代表性的点，原型聚类也称为基于原型的聚类/Prototype-based Clustering。原型聚类算法假设聚类结构能通过一组原型刻画，先对原型进行初始化，然后对原型进行迭代更新求解。采用不同的原型表示、不同的求解方式，将产生不同的算法。

4.1 k 均值算法

给定样本集 \(D = \{\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_m\}\)，\(k\) 均值算法针对聚类所得划分 \(C = \{C_1, C_2, \ldots, C_k\}\) 最小化平方误差

\[E = \sum_{i=1}^k\sum_{\boldsymbol{x}\in C_i} \lVert \boldsymbol{x} - \boldsymbol{\mu}_i \rVert_2^2,\]

其中 \(\boldsymbol{\mu}_i = \frac{1}{|C_i|}\sum_{\boldsymbol{x}\in C_i} \boldsymbol{x}\) 是簇 \(C_i\) 的均值向量。直观来看，平方误差刻画了样本围绕簇均值向量的紧密程度，\(E\) 值越小则簇内样本相似度越高。

但是，最小化上式是一个 \(\mathsf{NP}\) 难问题，因此 k 均值算法采用了贪心策略，通过迭代优化来近似求解。算法描述如下：

我们令需要求解的原型向量为均值向量，首先对均值向量进行初始化，然后在迭代过程中交替进行两个步骤：保持当前均值向量不变，计算每个样本与所有均值向量的距离，将其划入距离最近的簇；保持当前簇划分不变，更新每个簇的均值向量。重复上述过程直至收敛，即可得到最终的簇划分。对上述过程的重复可能设置对应阈值，例如最大迭代次数。

4.2 学习向量量化

与 k 均值算法类似，学习向量量化/Vector Quantization/LVQ 也试图找到一组原型向量来刻画聚类结构，但与一般聚类算法不同的是，LVQ 假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。

给定样本集 \(D = \{(\boldsymbol{x}_1,y_1), (\boldsymbol{x}_2,y_2), \ldots, (\boldsymbol{x}_m,y_m)\}\)，每个样本 \(\boldsymbol{x}_j\) 是由 \(n\) 个属性描述的特征向量 \((x_{j1}; x_{j2}; \ldots; x_{jn})\)，\(y_j \in \mathcal{Y}\) 是样本 \(\boldsymbol{x}_j\) 的类别标记。LVQ 的目标是学习得到一组 \(n\) 维原型向量 \(\{ \boldsymbol{p}_1, \boldsymbol{p}_2, \ldots, \boldsymbol{p}_q \}\)，每个原型向量代表一个聚类簇，簇标记 \(t \in \mathcal{Y}\)。

LVQ 的聚类生成过程受监督信息的辅助：随机选择样本，找出与其最近的原型向量，根据两者的类别标记是否一致来对原型向量进行相应的更新。具体算法描述如下：

我们考虑原型向量的更新过程，对样本 \(\boldsymbol{x}_j\)，若最近的原型向量 \(\boldsymbol{p}_r\) 与 \(\boldsymbol{x}_j\) 的类别标记相同，则令 \(\boldsymbol{p}_r\) 向 \(\boldsymbol{x}_j\) 的方向靠拢：

\[\boldsymbol{p}_r^{\prime} = \boldsymbol{p}_r + \eta \cdot (\boldsymbol{x}_j - \boldsymbol{p}_r),\]

新原型向量 \(\boldsymbol{p}_r^{\prime}\) 与 \(\boldsymbol{x}_j\) 之间的距离为 \((1-\eta) \cdot \lVert \boldsymbol{p}_r - \boldsymbol{x}_j \rVert_2\)，其中 \(\eta \in (0,1)\) 是学习率。若 \(\boldsymbol{p}_r\) 与 \(\boldsymbol{x}_j\) 的类别标记不同，则新原型向量与 \(\boldsymbol{x}_j\) 之间的距离将增大为 \((1+\eta) \cdot \lVert \boldsymbol{p}_r - \boldsymbol{x}_j \rVert_2\)，从而更远离 \(\boldsymbol{x}_j\)。

在学得一组原型向量 \(\{\boldsymbol{p}_1,\boldsymbol{p}_2,\ldots,\boldsymbol{p}_q\}\) 后，即可实现对样本空间 \(\mathcal{X}\) 的簇划分。对任意样本 \(\boldsymbol{x}\)，它将被划入与其距离最近的原型向量所代表的簇中；换言之，每个原型向量 \(\boldsymbol{p}_i\) 定义了与其相关的一个区域 \(R_i\)，该区域中每个样本与 \(\boldsymbol{p}_i\) 的距离不大于它与其他原型向量 \(\boldsymbol{p}_{i^{\prime}}(i^{\prime}\neq i)\) 的距离：

\[R_i = \{\boldsymbol{x}\in\mathcal{X}\mid||\boldsymbol{x}-\boldsymbol{p}_i||_2\leq||\boldsymbol{x}-\boldsymbol{p}_{i^{\prime}}||_2,i^{\prime}\neq i\}.\]

由此形成了对样本空间 \(\mathcal{X}\) 的簇划分 \(\{R_1,R_2,\ldots,R_q\}\)，该划分通常称为 Voronoi 剖分/Voronoi Tessellation。

若将 \(R_i\) 中的样本全用原型向量 \(\boldsymbol{p}_i\) 表示，则可实现数据的有损压缩/Lossy Compression，这称为向量量化，LVQ 也由此得名。

4.3 高斯混合聚类

高斯混合聚类/Mixture-of-Gaussian Clustering 采用概率模型来表达聚类原型，同样依赖对样本分布的假设。

回顾多元高斯分布：对 \(n\) 维样本空间 \(\mathcal{X}\) 中的随机向量 \(\boldsymbol{x}\)，若其服从高斯分布，则其概率密度函数为

\[p(\boldsymbol{x}) = \frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}e^{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\text{T}}\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})},\]

其中 \(\boldsymbol{\mu}\) 是 \(n\) 维均值向量，\(\Sigma\) 是 \(n\times n\) 的协方差矩阵。高斯混合分布则定义为

\[p_{\mathcal{M}}(\boldsymbol{x}) = \sum_{i=1}^k \alpha_i\cdot p(\boldsymbol{x}|\boldsymbol{\mu}_i,\boldsymbol{\Sigma}_i),\]

该分布由 \(k\) 个混合成分构成，每个混合成分对应一个高斯分布，其中 \(\boldsymbol{\mu}_i\) 与 \(\boldsymbol{\Sigma}_i\) 是第 \(i\) 个高斯混合成分的参数，而 \(\alpha_i > 0\) 为相应的混合系数/Mixture Coefficient，\(\sum_{i=1}^k \alpha_i = 1\)，保证了高斯混合分布是一个概率分布。

假设样本的生成过程由高斯混合分布给出：首先，根据 \(\alpha_1,\alpha_2,\ldots,\alpha_k\) 定义的先验分布选择高斯混合成分，其中 \(\alpha_i\) 为选择第 \(i\) 个混合成分的概率；然后，根据被选择的混合成分的概率密度函数进行采样，从而生成相应的样本。

因此高斯混合聚类所需的模型参数为 \(\{ (\alpha_i,\boldsymbol{\mu}_i,\boldsymbol{\Sigma}_i) \}_{i=1}^k\)，在得知这些参数之后，可以很容易地对样本空间进行簇划分。

若训练集 \(D = \{\boldsymbol{x}_1,\boldsymbol{x}_2,\ldots,\boldsymbol{x}_m\}\) 由上述过程生成，令随机变量 \(z_j \in \{1,2,\ldots,k\}\) 表示生成样本 \(\boldsymbol{x}_j\) 的高斯混合成分，其取值未知。显然，\(z_j\) 的先验概率对应于 \(\alpha_i\enspace (i=1,2,\ldots,k)\)。根据贝叶斯定理，\(z_j\) 的后验分布对应于

\[p_{\mathcal{M}}(z_j=i|\boldsymbol{x}_j) = \frac{P(z_j=i)\cdot p_{\mathcal{M}}(\boldsymbol{x}_j|z_j=i)}{p_{\mathcal{M}}(\boldsymbol{x}_j)} = \frac{\alpha_i\cdot p(\boldsymbol{x}_j|\boldsymbol{\mu}_i,\boldsymbol{\Sigma}_i)}{\sum_{l=1}^k \alpha_l\cdot p(\boldsymbol{x}_j|\boldsymbol{\mu}_l,\boldsymbol{\Sigma}_l)}.\]

这样，\(p_{\mathcal{M}}(z_j=i|\boldsymbol{x}_j)\) 给出了样本 \(\boldsymbol{x}_j\) 由第 \(i\) 个高斯混合成分生成的后验概率，记为 \(\gamma_{ji}\enspace (i=1,2,\ldots,k)\)。我们因此可以划分样本空间 \(\mathcal{X}\) 为 \(k\) 个簇 \(\mathcal{C} = \{C_1,C_2,\ldots,C_k\}\)，每个样本 \(\boldsymbol{x}_j\) 的簇标记 \(\lambda_j\) 如下确定：

\[\lambda_j = \underset{i\in\{1,2,\ldots,k\}}{\arg\max} \gamma_{ji}.\]

因此，高斯混合聚类事实上是采用概率模型（高斯分布）对原型进行刻画，划分规则则由原型对应的后验概率确定。下面将处理学习模型参数的问题。我们使用 EM 算法进行求解。

首先，给定样本集 \(D\)，可采用极大似然估计，即最大化对数似然

\[LL(D) = \ln\left(\prod_{j=1}^m p_{\mathcal{M}}(\boldsymbol{x}_j)\right) = \sum_{j=1}^m\ln\left(\sum_{i=1}^k \alpha_i\cdot p(\boldsymbol{x}_j|\boldsymbol{\mu}_i,\boldsymbol{\Sigma}_i)\right).\]

对于三个参数，我们用两次求偏导，一次拉格朗日乘子法，得到参数的更新公式：

先考虑每个高斯成分的均值 \(\mu_i\)，对 \(\mu_i\) 求偏导并令其为 0，有

\[\begin{aligned} \frac{\partial LL(D)}{\partial \mu_i} = 0 &\Rightarrow \sum_{j=1}^m \frac{\alpha_i\cdot p(\boldsymbol{x}_j|\boldsymbol{\mu}_i,\boldsymbol{\Sigma}_i)}{\sum_{l=1}^k \alpha_l\cdot p(\boldsymbol{x}_j|\boldsymbol{\mu}_l,\boldsymbol{\Sigma}_l)}(\boldsymbol{x}_j-\boldsymbol{\mu}_i) = 0, \\ &\Rightarrow \mu_i = \frac{\sum_{j=1}^m \gamma_{ji}\boldsymbol{x}_j}{\sum_{j=1}^m \gamma_{ji}}. \end{aligned}\]

类似处理高斯成分的协方差矩阵 \(\Sigma_i\)，有

\[\begin{aligned} \frac{\partial LL(D)}{\partial \Sigma_i} = 0 \Rightarrow \Sigma_i &= \frac{\sum_{j=1}^m \gamma_{ji}(\boldsymbol{x}_j-\boldsymbol{\mu}_i)(\boldsymbol{x}_j-\boldsymbol{\mu}_i)^{\text{T}}}{\sum_{j=1}^m \gamma_{ji}}. \end{aligned}\]

对于混合系数 \(\alpha_i\)，除了要最大化 \(LL(D)\)，还需满足 \(\alpha_i \geq 0\)，\(\sum_{i=1}^k \alpha_i = 1\)。考虑 \(LL(D)\) 的拉格朗日形式

\[L = LL(D) + \lambda\left(\sum_{i=1}^k \alpha_i-1\right),\]

其中 \(\lambda\) 为拉格朗日乘子。由上式对 \(\alpha_i\) 的导数为 0，有

\[\begin{aligned} \frac{\partial L}{\partial \alpha_i} = 0 &\Rightarrow\sum_{j=1}^m \frac{p(\boldsymbol{x}_j|\boldsymbol{\mu}_i,\boldsymbol{\Sigma}_i)}{\sum_{l=1}^k \alpha_l\cdot p(\boldsymbol{x}_j|\boldsymbol{\mu}_l,\boldsymbol{\Sigma}_l)} + \lambda = 0, \\ &\Rightarrow \alpha_i = \frac{1}{m}\sum_{j=1}^m \gamma_{ji}. \end{aligned}\]

也就是每个高斯成分的混合系数由样本属于该成分的平均后验概率确定。这就可以得到 EM 算法了：

在每步迭代中，先根据当前参数来计算每个样本属于各个高斯成分的后验概率 \(\gamma_{ji}\)（E步）；再根据后验概率和当前参数更新模型参数 \(\{(\alpha_i,\boldsymbol{\mu}_i,\boldsymbol{\Sigma}_i)\}_{i=1}^k\)（M步）。算法过程如下图所示：

算法第一行先对高斯混合分布的模型进行初始化，之后 repeat 循环内基于 EM 算法对模型参数进行迭代更新。若 EM 算法的停止条件满足（例如已达到最大迭代轮数，或似然函数值 \(LL(D)\) 增长很少甚至不再增长），接下来根据高斯混合分布计算出后验概率，根据后验概率确定簇标记并决定簇划分，最后返回最终结果。

5. 密度聚类

密度聚类也称为基于密度的聚类/Density-based Clustering，此类算法假设聚类结构能通过样本分布的紧密程度确定。通常情形下，密度聚类算法从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。

DBSCAN/Density-Based Spatial Clustering of Applications with Noise 基于一组临域参数 \((\epsilon,\text{MinPts})\) 来刻画样本分布的紧密程度。给定数据集 \(D = \{\boldsymbol{x}_1,\boldsymbol{x}_2,\ldots,\boldsymbol{x}_m\}\)，定义以下概念：

  • \(\epsilon\)-邻域：对 \(\boldsymbol{x}_i \in D\)，其 \(\epsilon\)-邻域包含样本集 \(D\) 中与 \(\boldsymbol{x}_i\) 的距离不大于 \(\epsilon\) 的样本，即 \(N_{\epsilon}(\boldsymbol{x}_i) = \{\boldsymbol{x} \in D \mid \text{dist}(\boldsymbol{x}_i,\boldsymbol{x}) \leq \epsilon\}\)；
  • 核心对象/Core Object：若 \(\boldsymbol{x}_i\) 的 \(\epsilon\)-邻域至少包含 \(\text{MinPts}\) 个样本，即 \(|N_{\epsilon}(\boldsymbol{x}_i)| \geq \text{MinPts}\)，则 \(\boldsymbol{x}_i\) 是一个核心对象；
  • 密度直达/Directly Density-reachable：若 \(\boldsymbol{x}_j\) 位于 \(\boldsymbol{x}_i\) 的 \(\epsilon\)-邻域中，且 \(\boldsymbol{x}_i\) 是核心对象，则称 \(\boldsymbol{x}_j\) 由 \(\boldsymbol{x}_i\) 密度直达；
  • 密度可达/Density-reachable：对 \(\boldsymbol{x}_i\) 与 \(\boldsymbol{x}_j\)，若存在样本序列 \(\boldsymbol{p}_1,\boldsymbol{p}_2,\ldots,\boldsymbol{p}_n\)，其中 \(\boldsymbol{p}_1 = \boldsymbol{x}_i\)，\(\boldsymbol{p}_n = \boldsymbol{x}_j\) 且 \(\boldsymbol{p}_{q+1}\) 由 \(\boldsymbol{p}_q\) 密度直达，则称 \(\boldsymbol{x}_j\) 由 \(\boldsymbol{x}_i\) 密度可达；
  • 密度相连/Density-connected：对 \(\boldsymbol{x}_i\) 与 \(\boldsymbol{x}_j\)，若存在 \(\boldsymbol{x}_k\) 使得 \(\boldsymbol{x}_i\) 与 \(\boldsymbol{x}_j\) 均由 \(\boldsymbol{x}_k\) 密度可达，则称 \(\boldsymbol{x}_i\) 与 \(\boldsymbol{x}_j\) 密度相连。

因为密度直达要求 \(\boldsymbol{x}_i\) 是一个核心对象，但是 \(\boldsymbol{x}_j\) 不一定是核心对象，所以密度直达一般不满足对称性，密度可达关系满足传递性但不满足对称性，密度相连关系满足对称性和传递性。

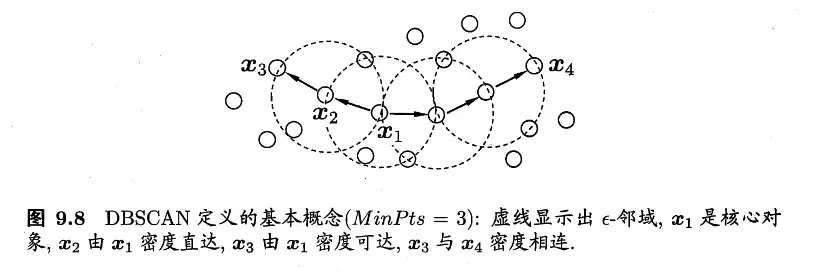
基于这些概念，DBSCAN 将簇定义为：由密度可达关系导出的最大的密度相连样本集合。给定邻域参数 \((\epsilon,\text{MinPts})\)，簇 \(C \subseteq D\) 是满足以下性质的非空样本子集：

  • 连接性/Connectivity：\(\boldsymbol{x}_i \in C\)，\(\boldsymbol{x}_j \in C\) \(\Rightarrow\) \(\boldsymbol{x}_i\) 与 \(\boldsymbol{x}_j\) 密度相连（也就是簇内任意两个样本都密度相连）；
  • 最大性/Maximality：\(\boldsymbol{x}_i \in C\)，\(\boldsymbol{x}_j\) 由 \(\boldsymbol{x}_i\) 密度可达 \(\Rightarrow \boldsymbol{x}_j \in C\)。

如何从数据集 \(D\) 中找出满足以上性质的聚类簇呢？实际上，若 \(\boldsymbol{x}\) 为核心对象，由 \(\boldsymbol{x}\) 密度可达的所有样本组成的集合记为 \(X = \{\boldsymbol{x}' \in D \mid \boldsymbol{x}' \text{ is density-connected by }\boldsymbol{x}\}\) 则很容易见得 \(X\) 即为包含 \(\boldsymbol{x}\) 的最大的密度相连样本集合。

于是，DBSCAN 算法先任选数据集中的一个核心对象为种子，由此出发确定相应的聚类簇，算法流程如下图所示：

算法首先确定所有核心对象，然后以任一核心对象为出发点，找出由其密度可达的样本生成聚类簇，直到所有核心对象均被访问过为止。

6. 层次聚类

层次聚类/Hierarchical Clustering 试图在不同层次对数据集进行划分，从而形成树形的聚类结果。数据集的划分可以采用自底向上的聚合策略，也可以采用自顶向下的分拆策略。

AGNES/AGglomerative NESting 是一种采用自底向上聚合策略的层次聚类算法。它先将数据集中的每个样本看作一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并，这个过程不断重复，直至达到预设的聚类簇个数。

算法的关键是如何计算聚类簇之间的距离，实际上，每个簇是一个样本集合，因此只需采用关于集合的某种距离即可。例如，给定聚类簇 \(C_i\) 与 \(C_j\)，可通过下面的式子来计算距离：

  • 最小距离：\(d_{\min}(C_i,C_j) = \min\limits_{\boldsymbol{x}\in C_i,\boldsymbol{z}\in C_j} \text{dist}(\boldsymbol{x},\boldsymbol{z})\)；
  • 最大距离：\(d_{\max}(C_i,C_j) = \max\limits_{\boldsymbol{x}\in C_i,\boldsymbol{z}\in C_j} \text{dist}(\boldsymbol{x},\boldsymbol{z})\)；
  • 平均距离：\(d_{\text{avg}}(C_i,C_j) = \dfrac{1}{|C_i||C_j|} \sum\limits_{\boldsymbol{x}\in C_i}\sum\limits_{\boldsymbol{z}\in C_j} \text{dist}(\boldsymbol{x},\boldsymbol{z})\)。

算法的具体流程如下图所示：

具体来讲，算法首先将每一个样本看作一个初始聚类簇，并且初始化对应的距离矩阵；然后在每一步找到距离最近的两额聚类簇进行合并，并且更新距离矩阵，重新编号簇并且更新距离矩阵，直到达到预设的聚类簇数。

显然，使用不同的距离，对赢得层次聚类算法的结果也不一样。当距离采用 \(d_{\min}\)、\(d_{\max}\) 或 \(d_{\text{avg}}\) 时，AGNES 算法被相应地称为单链接/Single-linkage、全链接/Complete-linkage 或均链接/Average-linkage 算法。